ARTÍCULOS DE INVESTIGACIÓN

 

Un vistazo a la Inferencia Bayesiana

 

A quick look at Bayesian Inference

 

 

Lizbeth Román Padilla^1,*
* Facultad de Ciencias Actuariales - Universidad Anáhuac, Ciudad de México, México
lizroman@hotmail.com
Artículo recibido: 2021-07-30     Artículo aceptado: 2021-09-07

 

 

---

Resumen

El enfoque Bayesiano de la estadística debe considerarse como una alternativa adicional al enfoque clásico, siendo ambos enfoques complementarios más no excluyentes. La estadística Bayesiana ofrece una gran variedad de métodos estadísticos similares en número a los proporcionados por el enfoque clásico.

La estadística Bayesiana debe su nombre al uso repetido del Teorema de Bayes: la distribución final o posterior es el resultado de aplicar el Teorema de Bayes a la información que proporcionan los datos (función de verosimilitud) y la información previa del parámetro de interés (distribución inicial). La distribución posterior es idónea para hacer cualquier tipo de inferencias sobre el parámetro de interés 1, ya sea estimación puntual o por intervalo, pues incluye toda la información disponible acerca de θ una vez observados los datos junto con la información inicial.

El objetivo de este artículo es la ejemplificación de obtención el estimador puntual Bayesiano y la región creíble de la media (θ) de datos con distribución Cauchy (θ,1). Para este propósito se usarán los datos de precipitaciones anuales del estado mexicano de Tabasco. Adicionalmente, se utilizan técnicas de simulación de variables aleatorias e integración numérica.

Los resultados obtenidos mediante inferencia Bayesiana permitirán tener una aproximación a la verdadera media de precipitación (θ) desde que el estimador clásico se vuelve inestable conforme incrementa el tamaño de muestra. Con este simple ejercicio se pretende dar a conocer algunas ventajas de aplicar los métodos Bayesianos.

Palabras clave: Algoritmo aceptación-rechazo; Estimador Bayesiano; Iniciales no Informativas; Inferencia Bayesiana; Regiones HPD; Simulación.

---

Abstract

The Bayesian approach to statistics should be considered as an additional alternative to the classical approach, both approaches being complementary but not exclusive. Bayesian statistics offers a great variety of statistical methods similar in number to those provided by the classical approach.

The origin of the term 'Bayesian Statistics' is due to the repeated use of the Bayes Theorem: the final or posterior distribution is the result of applying the Bayes Theorem to the information provided by data (likelihood function) and initial information about the parameter of interest (distribution initial).

Posterior distribution is ideal for making any kind of inferences about the parameter of interest, whether it can be a point estímate or by interval, since it includes all the information available about θ after data has been observed together with initial information.

The objective of this article is to illustrate how to get a Bayesian point estimator and credible region for the mean (θ) of Cauchy data Cau(θ, 1). For this purpose, annual rainfall data of Tabasco (Mexican state) will be used. Additionally, random variable simulation techniques and numerical integration are employed.

The results obtained through Bayesian inference provides us with an approximation to the trae mean of precipitation (θ) since the classical estimator becomes unstable as the sample size increases. This simple exercise is intended to show some advantages of applying Bayesian methods.

Keywords: Acceptance-Rejection algorithm; Bayesian estimation; Non-Informative Priors; Bayesian Inference; HPD regions; Simulation

---

 

 

INTRODUCCIÓN

Filosofía bayesiana

Al igual que en los métodos estadísticos clásicos de inferencias, existe otro acercamiento a la inferencia conocido como inferencia bayesiana. La cual tiene tres características fundamentales heredadas del enfoque bayesiano de la estadística:

•     La inferencia bayesiana, y en general la estadística bayesiana, se fundamenta en la interpretación subjetiva de la probabilidad, es decir la probabilidad describe un grado de creencia, y al contrario del enfoque clásico, no se basa en el límite de las frecuencias relativas o en la descripción de problemas físicos (interpretación clásica y frecuentista de la probablidad, respectivamente).

•     Bajo el supuesto de que los datos siguen un modelo estadístico indexado por algún parámetro θ (desconocido). En el enfoque bayesiano, los parámetros son tratados como variables aleatorias, es decir, se les atribuye un grado de incertidumbre y por tanto se les puede asociar una distribución de probabilidad.

•     Y, finalmente, al obtener una distribución de probabilidad del parámetro de interés, se pueden hacer inferencias acerca de su verdadero valor o sobre cualquiera de sus propiedades.

Método bayesiano

Suponga que x'= (x₁, x₂ ,..., x_n) es un vector de n observaciones cuya distribución de probabilidad p(x|θ) que depende de k parámetros θ' = (θ₁, θ₂ ,...,θ_k). Suponga, además que θ' cuenta por sí misma con una función de distribución π(θ'). Entonces,

Entonces, dados los datos observados x, la distribución condicional de θ es

y p (x ) puede ser

donde la suma o la integral toma todos los posibles valores de θ.

La ec. (2) puede escribirse de manera equivalente como

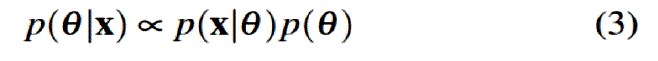
donde el símbolo "" se refiere a que el lado derecho de la ecuación es aproximado, salvo la constante que normaliza a π(θ | x) para que el área bajo la curva (o la suma) sea uno. A la ec. (2) se le conoce como el Teorema de Bayes y sus elementos son:

•     La función se le llama distribución inicial o prior, y nos dice todo lo que se sabe acerca de θ antes de haber observado los datos.

•     La función π(θ | x) es la distribución posterior o final, y es la que proporciona información acerca de θ dado el conocimiento de los datos.

•     Dados los datos, la función p (x | θ) puede verse como función solamente de θ, y se le llama función de verosimilitud de θ dado x, la cual se puede escribir como l (θ | x).

Es decir, el Teorema de Bayes asegura que la distribución de probabilidad posterior de 0 dado x es proporcional al producto de la verosimilitud y la inicial:

Esta expresión permite formular matemáticamente cómo la información inicial puede combinarse con la información que proveen los datos. La función de verosimilitud es la que a través de ella los datos x modifican el conocimiento previo de θ, es decir, es la información de θ que proporciona los datos. Por tanto, juega un papel importante dentro del Teorema de Bayes.

El Teorema de Bayes describe el proceso de aprendizaje a través de la experiencia. (Box y Tiao, 1992, Secc. 1.2.2).

Inferencia bayesiana

La inferencia bayesiana hace uso de la Teoría de la Decisión, pues al elegir un estimador dentro de un conjunto de posibles estimadores del parámetro θ(o de alguna función de este), a esa elección se le asocia una ganancia o pérdida que a su vez dependerá del estado de la naturaleza, es decir, el verdadero valor del parámetro θ. La distribución de probabilidad posterior refleja el conocimiento del tomador de desiciones, pues es el resultado de combinar la información inicial junto con la información que proveen los datos acerca del parámetro. Por tanto, se espera que el tomador de desiciones elija la acción que maximice (minimice) su beneficio.

La inferencia bayesiana proporciona una forma satisfactoria de introducir explícitamente y mantener los supuestos acerca del conocimiento previo o de la ignorancia. (Box y Tiao, 1992).

Estimadores bayesianos

Si uno desea hacer inferencia bayesiana puntual, comenzará por definir la función de pérdida y deberá encontrar el estimador bayesiano que la minimice (una mejor aproximación a la Teoría de Decisión bayesiana puede encontrarla en Mood et al., 1974 y Box and Tiao, 1992).

El estimador bayesiano más común es la esperanza de la distribución posterior π(θ | x) pues es el que minimiza la pérdida esperada cuadrática. Sin embargo, el estimador bayesiano dependerá de la función de pérdida utilizada.

Conjuntos (creíbles) HPD

Otra forma común de inferencia es presentar intervalos de confianza para θ. El análogo bayesiano a los intervalos de confianza clásicos son los llamados conjuntos creíbles 100 (1 - α) % para θ. Un conjunto creíble es un subconjunto C ∈ Θ tal que P (C | x) > 1 - α (Def. 4 en Berger, 2010). Note que se está trabajando directamente con la distribución posterior π(θ | x), por tanto, tiene sentido interpretarlo como la probabilidad (posterior) de que θ se encuentre en C. Recuerde que los intervalos de confianza se interpretan en función de la cobertura de probabilidad, véase las secciones 1.6 y 4.1 de (Berger, 2010).

De los posibles conjuntos creíbles para θ se elige el conjunto con volumen más pequeño tal que contenga a los valores de θ más probables. Los intervalos HPD (siglas en inglés, highest posterior density) son conjuntos creíbles 100( 1 - α ) % de θ, C ∈ Θ, de la forma C={θ∈ Θ: π(θ | x)) ≥ k(α)} siendo k(α) la constante más grande que cumpla con que P(C | x) > 1 - α. Los conjuntos creíbles generalmente son fáciles de calcular y algunas veces on la única alternativa a sus contrapartes clásicas (Berger, 2010).

Inferencia sobre θ de Cauchy (θ,1)

Distribución Cauchy

Consideraremos el problema de hacer inferencias acerca del parámetro de localización θ de la distribución Cauchy.

La distribución Cauchy pertenece a la familia de distribuciones de localización y escala, además de que carece de media y varianza asimismo no cuenta con función generadora de momentos. Las estimaciones muestrales de la media y la varianza crecen conforme se incrementa el tamaño de muestra y se vuelven inestables (Wikipedia contributors 2021, July 6) y el método de máxima verosimilitud implica encontrar las raíces de polinomios de grado mayor, donde las raíces pueden ser máximos locales pero no necesariamente globales. Otra característica de la distribución Cauchy es que pertenece a la familia de distribuciones estables. Una distribución de probabilidad se dice estable si una combinación lineal de dos variables aleatorias independientes de esta distribución tiene la misma distribución, salvo algún parámetro de localización o de escala, véase la Def. 16.20 en (Klenke, 2014).

La familia de distribuciones estables son adecuadas para modelar datos con colas pesadas y sesgadas (Ball et al., 2021) en hidrología. Específicamente, la distribución Cauchy se utiliza para modelar eventos extremos, tales como el máximo anual de caida de lluvia en un dia (Wikipedia contributors. 2021, July 6).

Inferencia bayesiana: Cauchy

Suponga que se tiene una muestra aleatoria X₁, X₂,..., X_n provenientes de una distribución Cauchy con parámetro θ desconocido y varianza conocida e igual a uno, . El objetivo es hacer inferencias acerca del parámetro de localización θ. Se utilizará una distribución inicial no informativa definida en el espacio restringido de θ > 0 desde que θ es un parámetro de localización. Un resumen completo sobre la selección de las distribuciones iniciales puede verse en (Kass, R., y Wasserman, L.,1996). La densidad posterior de θ dado x = (x₁, x₂ ,..., x_n) estará dada por

Ejemplo. Datos de precipitación

La Tabla No. 1 muestra las precipitaciones anuales registradas durante 36 años en el estado mexicano de Tabasco, el cual se caracteriza por ser uno de los estados con más precipitaciones en un año. Suponga que las precipitaciones siguen una distribución Cauchy con parámetro de localización desconocido (θ) y varianza conocida e igual a uno (σ² = 1).

En análisis descriptivo sobre los datos de precipitación puede verse en la Figura No.1. La gráfica izquierda muestra las precipitaciones normalizadas (eje X) vs. la densidad Cauchy(0,1). La gráfica de caja y bigote (centro) muestra una distribución ligeramente sesgada a la derecha e identifica una observación aberrante. Finalmente, la gráfica de control (derecha) muestra claramenta al outlier que rebasa tres desviaciones estándares mientras que el resto de las observaciones no rebasan dicha franja.

Aproximación numérica de π(θ | x)

Mediante aproximación numérica (Narasimhan, B. (n.d.)) se obtiene una estimación de la constante de integración (denominador de la ec. (4)) y por tanto una aproximación a la distribución posterior π(θ | x), véase la Figura No. 2 (línea roja). Mediante el algoritmo de aceptación-rechazo (véase secc. 4.4 de Ross, 1999) se generaron m = 10,000 variables aleatorias de una distribución de cobertura y se aceptaron n = 7782 variables provenientes de la distribución π(θ | x), {θ₁, θ₂,..., θ₇₇₈₂}, histograma de la Figura No. 2. La región HPD al 95% se obtiene a partir de los valores simulados θ_i(i = 1, ... 7782), al igual que se obtienen los cuantiles q_0.025 y q_0,975, (véase la función hdi dentro del paquete HDInterval del lenguaje de programación R, M., M., & J., K.).

El estimador bayesiano puntual de θ puede ser la mediana o la media muestral posteriores, θ_mediana = 2130.71 y θ_media = 2130.86, respectivamente, ya que ambos son muy similares. Por otro lado, el intervalo HPD al 95% es (2126.09 , 2135.45) que difiere muy poco de los cuantiles (q_0.025 , q_0,975) = (2126.09 , 2135.45). Sin embargo, el intervalo HPD contendrá con una probabilidad del 95% al verdadero valor θ una vez que se han observado los datos.

 

CONCLUSIONES

La inferencia bayesiana es una herramienta útil cuando se desea saber el verdadero valor del parámetro θ asociado a alguna distribución de probabilidad que siguen algunos datos. La idea principal es que la distribución posterior π(θ | x) contiene toda la información disponible sobre θ, información que proviene tanto de los datos como de la información inicial del parámetro. Por tanto, cualquier inferencia sobre θ puede obtenerse de π(θ | x). Incluso cuando se requiera estimar puntualmente o por intervalos.

El uso más simple de un proceso inferencial de la distribución posterior es reportar un estimador puntual para θ, la elección del estimador puntual se asocia a una función de pérdida, pues el proceso de selección incurre en un pérdida (o ganancia) por haber obrado de tal manera. La media y la mediana de π(θ | x) son los estimadores bayesianos de las funciones de pérdida cuadrática y pérdida absoluta, respectivamente. En caso de requerir estimar un intervalo, los intervalos {creíbles) HPD son los equivalentes a los intervalos clásicos de confianza, salvo que difieren en su interpetación, pues las regiones creíbles contienen al valor de θ con una probabilidad posterior 1 - α, muy distinto a la interpretación frecuentista de su contraparte clásica.

Los resultados obtenidos mediante inferencia bayesiana permitien tener una aproximación a la verdadera media de precipitación (θ) desde que los parámetros de la distribución Cauchy no se corresponden a la media y varianza, Wikipedia contributors. (2021, July 6). Por tanto, no se pueden estimar mediante la media y varianza muestrales.

Finalmente, con este simple ejercicio se pretende dar a conocer algunas ventajas de aplicar los métodos bayesianos.

 

DISCUSIÓN

La inferencia bayesiana es una respuesta a las inferencia clásica cuando ésta no proporciona de una respuesta adecuada. Debido a que los métodos bayesianos funcionan de la misma forma; se determina una distribución inicial que proporcione la información del parámetro antes de observar los datos, el Teorema de Bayes permite construir la distribución (de probabilidad) final a partir de la información proporcionada por los datos y la distribución inicial. En este artículo, encontramos una solución al problema de inferir el verdadero valor del parámetro θ de una distribución cuando se trabaja desde el enfoque clásico, y como se mostró, la inferencia bayesiana proporcionó estimaciones puntuales y por intervalo.

En general, los métodos bayesianos son una alternativa válida a algunas deficiencias de los métodos clásicos (Gómez-Villegas, 2006). Sin embargo, ambos enfoques no son excluyentes, deben ser complementarios.

 

NOTAS

¹ Lizbeth Román Padilla es doctora en Estadística (Estadística Bayesiana Objetiva) por la Universidad de Valencia, España. Maestra en Méts. Matemáticos en Finanzas (Universidad Anáhuac) y Actuaría (Facultad de Ciencias, UNAM). Ha hecho dos posdoctorados (Francia y México) y desde 2013 es docente en los niveles de licenciatura y posgrado. https://orcid. ore/0000-0001-9673-4209

 

REFERENCIAS BIBLIOGRÁFICAS

Ball,C.,Rimal,B.,yChhetri,S.(2021).Anew generalized cauchy distribution with an application to annual one day maximum rainfall data. Statistics, Optimization and Information Com- puting, 9, pp. 123-136. https://doi.org/10.19139/soic-2310-5070-1000.        [ Links ]

Berger, J. (2010). Statistical decision theory and bayesian analysis (2nd). Springer-Verlag: New York, EEUU.        [ Links ]

Box, G.,y Tiao, G. (1992). Bayesian inference in statistical analysis. Wiley-Interscience.        [ Links ]

Kass, R., y Wasserman, L. (1996). The selection of prior distributions by formal rules. Journal of the American Statistical Association, 91(435), pp. 1343-1340. https://doi.org/10.2307/2291752.        [ Links ]

Klenke, A. (2014). Probability theory. A comprehensive course. (2nd). Springer-Verlag: London, UK.        [ Links ]

Gómez-Villegas, M.A. (2006). ¿Por qué la inferencia estadística bayesiana? Boletín de la Sociedad de Estadística e Investigación Operativa, 22, 1, pp. 6-8.        [ Links ]

M., M., y J., K. (n.d.). Highest (posterior) density intervals. Retrieved July 20, 2021, from https:// cran.r-project.org/ web/packages/HDInterval/ HDInterval. pdf.        [ Links ]

Mood, A., Graybill, F., y Boes, D. (1974). Introduction to the theory of statistics (3rd). McGraw- Hill.        [ Links ]

Narasimhan, B. (n.d.). Adaptive multivariate integration over hypercubes. Retrieved July 19, 2021, from https://bnaras.github. io/cubature/.        [ Links ]

Ross, S. (1999). Simulación (2a.). Prentice Hall: México.        [ Links ]

Wasserman, L. (2004). All of statistics. A concise course in statistical inference. Springer Science+Business Media: New York, EEUU.        [ Links ]

Wikipediacontributors. (2021, July 6). Cauchy distribution. In Wikipedia, The Free Encyclopedia. Retrieved 00:23, August 31, 2021, from https://en.wikipedia.org/w/index.php?title=Cauchy_distribution& oldid=1032217044.