ARTÍCULOS DE INVESTIGACIÓN

 

Un problema en la estimación del parámetro de forma
del modelo normal - asimétrico

 

 

Dr.(c) Omar Chocotea Poca¹ & Mgtr. Iván Yony Aliaga Casceres^2
1Instituto de Estadística, Universidad de Valparaíso, Chile y Carrera de Estadística, Universidad
Mayor de San Andrés, Bolivia   omar.chocotea@postgrado.uv.cl
²Carrera de Estadística, Universidad Mayor de San Andrés, Bolivia

 

 

---

Resumen

El modelo normal-asimétrico es adecuado cuando la estructura de los datos presenta una moda y asimetría. En esta nota se observa la existencia de un problema de estimación del parámetro de forma utilizando el método de momentos en tamaños de muestra pequeños contemplando algunos aspectos de Gupta & Gupta (2008) [Test,17, 197-210].

Palabras clave: Modelo asimétrico; problema de estimación

---

Abstract

The normal-asymmetric model is suitable when the data structure presents a mode and asymmetry. This note shows the existence of an estimation problem of the shape parameter using the method of moments in small sample sizes, contemplating some aspects of Gupta & Gupta (2008) [Test, 17, 197-210].

Keywords: Asymmetric model; estimation problem

---

 

 

1. INTRODUCCIÓN

El interés por la clase de distribuciones normalasimétricay relacionadas ha crecido enormemente, el estudio de sus propiedades continúa, varias de sus propiedades permiten tener por ejemplo las propiedades de la distribución normal (ver Azzalini, 2014; Arellano-Valle etal., 2018).

La distribución normal-asimétrica de Azzalini (1985) contempla un parámetro de asimetría/forma: Una variable aleatoria (v.a.) Z tiene una distribución normal-asimétrica estándar con parámetro de forma λ ∈ R, y representaremos por Z ~NA(λ), si su función de densidad de probabilidad (fdp) está dada por

donde φ(.) y Φ(.) denotan la fdp y la función de distribución acumulada de la distribución normal estándar (N(0, 1)). Al asumir λ = 0 se tiene como caso especial a la distribución N(0,1). La fdp de la distribución NA(λ) es una densidad unimodal que está sesgada a la izquierda si λ < 0, y sesgada a la derecha si λ > 0. La esperanza y la varianza de Z ~ NA(λ), están dadas por

y

respectivamente, donde

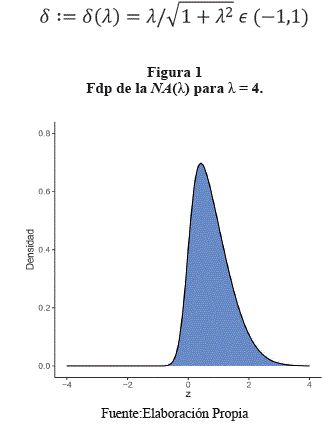
Si Z ~NA(λ), entonces la v.a. Y = ξ + ωZ tiene una distribución normal-asimétrica con parámetros de localización ξ, ∈ R, escala ω ∈ R₊, y forma λ ∈ R, y representaremos por Y-NA(ξ,ω,λ). La fdp de Y-NA (ξ,ω,λ) está dada por

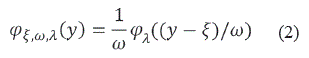
El siguiente resultado proporciona algunas propiedades para la distribución Z~NA(λ).

Si Z~NA(λ), entonces las siguientes propiedades son verdaderas: φ_λ(0) = φ(O) para todo λ; -Z~NA(-λ), equivalente a φ_λ(-z) = φ_-λ(z) para todo z; y Z²-X²₍₁₎ independientemente de λ.

En la Sección 2, analizamos al estimador de momentos del parámetro de asimetría de la distribución normal-asimétrica, también, en el escenario de una muestra aleatoria extraída de una población normal-asimétrica presentamos la densidad y la función generatriz de momentos (fgm) de la media muestral. En la Sección 3, se efectúa un estudio de simulación para verificar el problema de estimación del parámetro de asimetría vía el método de momento. La Sección 4 ofrece una conclusión.

 

2. EL ESTIMADOR DE MOMENTO

Cuando Z ~ NA(λ), el estimador de momento de λ es la solución de

donde

es la media muestral, y la solución existe si y solamente si

Chen et al. (2004) incorporan las siguientes proposiciones.

Proposición 1. Sea Z₁,Z₂, . . . ,Z_n una muestra aleatoria procedente de la NA(λ), entonces la fdp de está dada por

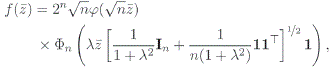
donde Φ_n(.) denota lafda de la N_n(0, I_n), I_n es la matriz identidad, y 1 = (1, . . . , 1)^T.

Proposición 2. Sea Z₁ . . . ,Z_n una muestra aleatoria procedente de la NA(λ), entonces la fgm de está dada por

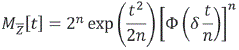
De las Proposiciones 1 y 2 se observa que la distribución de no es conocida y no es fácil de establecer (ver Gupta & Chen, 2003; Chenetal., 2004).

Por el Teorema del Límite Central, la distribución asintótica de

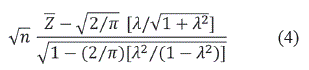
es N(0, 1). Por lo tanto, cuando el tamaño de la muestra n es lo suficientemente grande, aunque la distribución exacta de la media muestral estandarizada no es una distribución normal-asimétrica, su distribución asintótica sigue una distribución N(0, 1) (ver Gupta & Chen, 2003; Chen etal., 2004).

 

3. ESTUDIO DE SIMULACIÓN

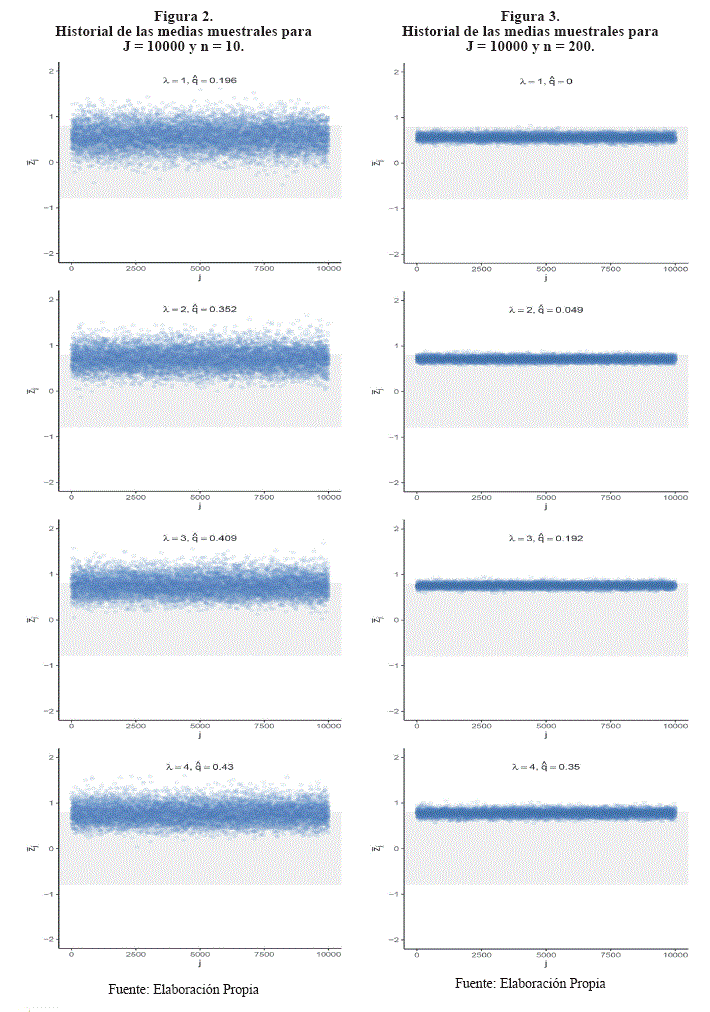
Basado en J=1000, 5000, 10000 conjuntos de datos, con los valores n=10, 20, 30, 40, 50, 100, 200 y λ = 1,2,3,4, se estima

Los resultados se muestran en el cuadro siguiente. Las figuras siguientes muestran el historial de las medias muestrales para J = 10000 conjuntos de datos y n = 10, 200, donde la banda ploma en el eje vertical inicia en   y termina en

Los resultados indican que: a) si aumenta el tamaño de la muestra disminuye , y b) si aumenta parámetro de asimetría aumenta .

 

4. CONCLUSIÓN

En esta nota hemos analizado una opción de estimación del parámetro de asimetría de la distribución normal-asimétrica de Azzalini (1985), se observa que se tiene algunos problemas al estimar el parámetro de asimetría en tamaños de muestra moderados. Otros problemas de estimación pueden revisarse en Pewsey (2000), Monti (2003), Liseo & Loperfido (2006), y Sartori (2006).

Algunas alternativas de estimación se ven por ejemplo en Azzalini (2014) y Arellano-Valleetal. (2018).

 

AGRADECIMIENTOS

El primer autor fue parcialmente apoyado por la beca FIB-UV de la Universidad de Valparaíso, Chile. Los autores agradecen al editor por los útiles comentarios

 

BIBLIOGRAFÍA

1.   Arellano-Valle, R. B., Ferreira, C. S., & Genton, M. G. (2018). Scale and Shape Mixtures of Multivariate Skew-Normal Distributions. Journal of Multivariate Analysis, 166, 98-110. 1,4        [ Links ]

2.   Azzalini, A. (1985). A Class of Distributions which Includes The Normal Ones. Scandinavian Journal of Statistics, 12(2), 171-178. 1, 4        [ Links ]

3.   Azzalini, A. (2014). The Skew-Normal and Related Families. Cambridge: Cambridge University Press. 1, 4        [ Links ]

4.    Chen, J. T., Gupta, A. K., & Nguyen, T. T. (2004). The Density of The Skew Normal Sample Mean and its Applications. Journal of Statistical Computation and Simulation, 74(7), 487-494.2        [ Links ]

5.    Gupta, A. & Chen, T. (2003). On The Sample Characterization Criterion for Normal Distributions. Journal of Statistical Computation and Simulation, 73(3), 155-163. 2        [ Links ]

6.    Gupta, R. D. & Gupta, R. C. (2008). Analyzing Skewed Data by Power Normal Model. Test, 17, 197-210.1        [ Links ]

7.    Liseo, B. & Loperfido, N. (2006). A Note on Reference Priors for The Scalar Skew-Normal Distribution. Journal of Statistical Planning and Inference, 136(2), 373-389. 4        [ Links ]

8.   Monti, A. C. (2003). A Note on The Estimation of The Skew Normal and The Skew Exponential Power Distributions. METRON - International Journal of Statistics, LXI(2), 205-219.4        [ Links ]

9.    Pewsey, A. (2000). Problems of Inference for Azzalini 's Skewnormal Distribution. Journal of Applied Statistics, 27(7), 859-870. 4        [ Links ]

10.  Sartori, N. (2006). Bias Prevention of Maximum Likelihood stimates for Scalar Skew Normal and Skewt Distributions. Journal of Statistical Planning and Inference, 136(12), 4259-4275. 4        [ Links ]