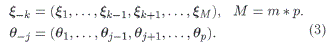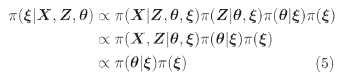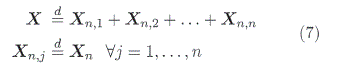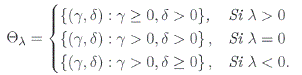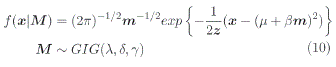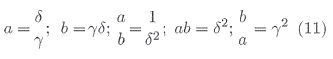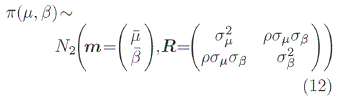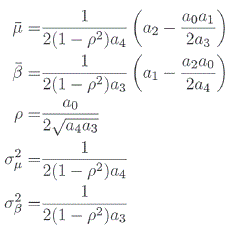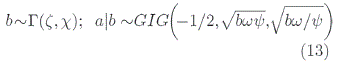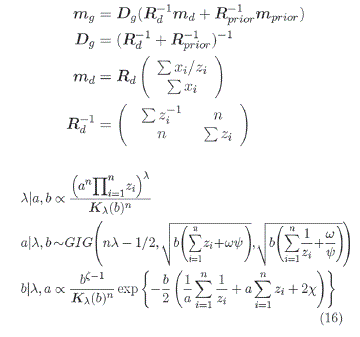Revista Varianza
versión impresa ISSN
9876-6789
Revista Varianza n.17 La Paz nov. 2020
ARTÍCULOS DE INVESTIGACIÓN
Estimación de los parámetros de la distribución
de cambios de precios mensuales del índice de
precios al consumidor de Bolivia
Mgtr. Iván Yony Aliaga Casceres* & Dr.(c) Omar Chocotea Poca**
* Carrera de Estadistica, Universidad Mayor de San Andrés
 iyaliaga@umsa.bo, powervan@gmail.com
iyaliaga@umsa.bo, powervan@gmail.com
** Instituto de Estadistica, Universidad de Valparaiso
 ochocotea@umsa.bo
ochocotea@umsa.bo
Resumen
La presente investigación estima los parámetros de localización, asimetría y los grados de libertad de una distribución tipo G mediante un método de estimación de libre verosimilitud Bayesiana comparada con el clásico método Metropolis Hastings, utilizando para ello datos de la distribución de la variación mensual del Índice de Precios al Consumidor del Instituto Nacional de Bolivia, periodo ene-1986 a oct-2020, base 2016. Se evidenció que el proceso iterativo algorítmico para el método Metropolis Hastings es más eficiente, sin embargo, el mejor ajuste se encontró con el método ABC-GIBBS.
Palabras clave:
Analisis Bayesiano, Estimación de libre verosimilitud, Distribución tipo G.
Abstract
The present investigation estimates the location parameters, asymmetry and the degrees of freedom of a G-type distribution using a Bayesian free likelihood estimation method compared to the classic Hastings Metropolis method, using data from the distribution of the monthly variation of the Index of Consumer Prices of the National Institute of Bolivia, period Jan-1986 to Oct-2020, base 2016. It was evidenced that the algorithmic iterative process for the Metropolis Hastings method is more efficient, however, the best fit was found with the ABC method -GIBBS.
Keywords: Bayesian analysis, Free likelihood estimation, Type G distribution.
1. INTRODUCCIÓN
La familia de distribución tipo G fue estudiada por Marcus (1987), Andrews et al. (1974), y Rosinski (1991), es el producto entre dos variables aleatorias independientes, la primera con distribución Normal con varianza constante y la segunda con una deter- minada distribución de probabilidad cuyo espacio soporte está definido en los reales positivos.
La estimación de los parámetros de la familia de distribuciones tipo G es una tarea tediosa, el problema radica en la función de verosimilitud, los métodos de optimización estándar fallan al estimar todos los parámetros y el costo computacional es bastante alto, Barndorffetal. (198 1),Andrew setal. (1974).
Bajo un enfoque Bayesiano, un parámetro es visto como una variable aleatoria a la que antes de extraer alguna evidencia muestral, se le asigna una distribución previa, con base a un cierto grado de creencia con respecto al comportamiento aleatorio, cuando se obtiene la evidencia muestral surge una actualización en base a la distribución previa y la evidencia muestral, de esta manera se obtiene una nueva distribución llamada distribución posterior.
Existen varios métodos en el ámbito Bayesiano que aproximan la distribución posterior, en este aspecto se presenta los llamados métodos de verosimilitud libre, Rubin (1984), Diggle et al. (1984), Tavare et al. (1997), Beaumont et al. (2002), Ratmann et al. (2009), que aproximan de forma iterativa a la distribución posterior teórica resultante.
El término Cálculo Bayesiano Aproximado(ABC) fue establecido por los autores: Beaumont et al. (2002), quienes amplían aún más la metodología de los métodos de verosimilitud libre. El ABC es una técnica de aproximación a la distribución posterior de los parámetros de manera iterativa cuando la misma no tiene una función de verosimilitud explícita. Existen diferentes métodos de verosimilitud libre propuestos por diferentes autores: ABC-MCMC, Marjoram et al. (2003), ABC-GIBBS, Turner et al. (2012), Turner & Sederberg (2014). Este último es utilizado en esta investigación.
Los métodos: Metropolis Hastings, Hastings (1970), y ABC-GIBBS, Turner et al. (2012), Turner & Sederberg (2014), son aplicados en la estimación de los parámetros de la distribución de cambios de precios mensuales del Indice de Precios al consumidor de Bolivia desde ene-1986 hasta oct-2020, distribución teórica que presenta asimétria y leptocúrtosis, Blattberg et al. (1974), Kyprianou (2014).
2. MARCO TEÓRICO
2.1. Enfoque Bayesiano
Definición 2.1 Teorema de Bayes. Sean X y 0 variables aleatorias con función de probabilidad f(x\θ) y π(θ), entonces la distribución posterior está dada por:

donde θ vector de parámetros y Θ espacio paramétrico.Para aproximar π(θ | X) se recurre a una serie de métodos aproximados iterativos.
2.2. Método Metropolis Hastings
Este método es una generalización del método Hastings, Metropolis et al. (1953), utiliza una función de densidad propuesta que depende del estado actual de θ(t). La función de densidad q(θ*|θ(t)) puede ser tan simple como una función de densidad Normal localizada en θ(t).

2.3. Método ABC-GIBBS
El Algortimo ABC-GIBBS fue propuesto por Turner & Zandt (2014), los autores proponen extraer muestras aleatorias directamente de la distribución posterior condicional de los hiperparámetros1 que no dependan de la función de verosimilitud utilizando el método de Gibbs, Voss (2013), Beaumont et al. (2002), Marjoram et al. (2003), Ratmann et al. (2009), Sisson et al. (2007),Turner & Zandt (2014), Gelman et al. (2013).
Definición 2.2 Sea = (θ1,θ2,...,θp) el vector de parámetros, bajo un nivel de jerarquía de estos parámetros se tiene la siguiente notación para los hiperparámetros, de cada j-ésimo parámetro.
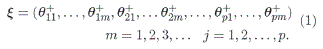
Ambos vectores pueden representarse como:
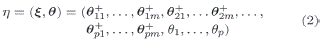
El vector de hiperparámetros y parámetros sin un elemento k-ésimo y j-ésimo respectivamente se denota por:
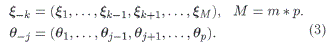
Utilizando el muestreo de Gibbs para obtener un gran número de muestras de 3 y es denotado por:
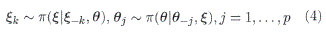
La implementación del método ABC-GIBBS se realiza en dos etapas, la primera etapa consiste de hallar la distribución condicional posterior de los hiperparámetros, tomando en cuenta que ξ, influye a X solo a través de θ, la distribución condicional posterior de ξ, no depende de la verosimilitud π(X,Z|θ, ξ) ya que es constante respecto a ξ.
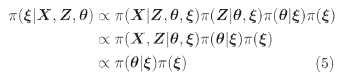
En la segunda etapa del método ABC-GIBBS comprende en hallar la distribución posterior de los parámetros, y debe tomarse en cuenta la dependencia condicional de θ y X, la densidad del parámetro ξ es constante con respecto a θ.


2.4. Distribuciones tipo G
Definición 2.3 Una variable aleatoria X con función de distribución de probabilidad F es infinitamente divisible (i.d.) si para todo n∈ N existe n variables aleatorias independientes e idénticamente distribuidos Xn,1,Xn,2,..,Xn,n tal que.
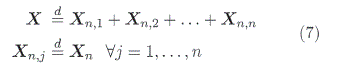
donde Xn representa la variable aleatoria con distribución factor común.
Definición 2.4 Una variable aleatoria continua X tiene distribución de probabilidad tipo G, si está definida como:
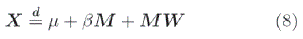
donde M y W son variables aleatorias independientes, W tiene distribución normal con varianza constante, M es una variable aleatoria con una determinada distribución de probabilidad con espacio soporte en los reales positivos y cumple la propiedad de infinita divisibilidad, el parámetro ju es el parámetro de localización, β es el parámetro de simetría o asimetria.
La variable aleatoria M tiene distribución Gaussiana Inversa Generalizada y cumple la propiedad infinita divisibilidad, Barndorff et al. (1977), Grosswald (1976).
2.5. Distribución Gaussiana Inversa Generalizada
Definición 2.5 Una variable aleatoria X tiene distribución Gaussiana Inversa Generalizada (GIG) con parámetros X, ó, y, si la función de densidad está dado por.

donde Kλ(·) es la función Bessel de tercer orden y (γ,δ) ∈ Θλ .
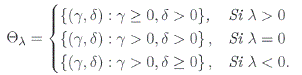
Proposición 2.1 Si M~GIG(λ=−ν/2,δ,γ=ν),ν> 0 y δ→0+ entonces M tiene distribución Gamma Inversa con parámetros (ν/2, ν/2).
Para obtener la distribución previa y la distribución posterior se identifíca la función conjunta de X y M, Hichen (2006).
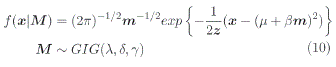
Realizando un cambio de variable en términos de a y b.
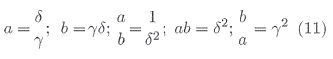
Se tiene la siguiente la función previa bivariantecona0, a1, a2, a3, a4 hiperparámetros.
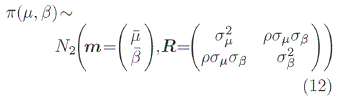
donde:
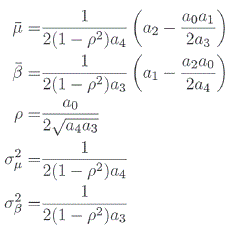
Para la distribución previa conjunta π(λ, a, b) se asume que tiene distribución conjugada a la distribución GIG, esto por razones analíticas.
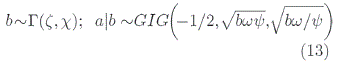
Para obtenerla distribución posterior conjunta de los parámetros µ, β y λ, a, b se realiza de forma separada al ser independientes ambos conjuntos de parámetros por construcción de la distribución tipo G.

donde
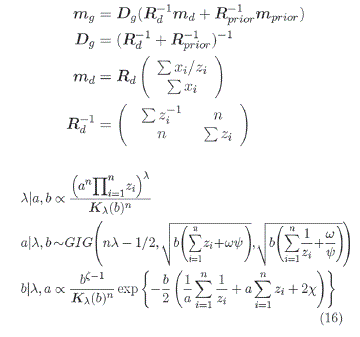
3. RESULTADOS
Se aplican los dos métodos anteriormente descritos en la estimación de parámetros de la distribución de cambios de precios (varianciones mensuales) del Índice de Precios al Consumidor con periodicidad desde Ene-1986 hasta Oct-2020, con base 2016=100 del Instituto Nacional de Estadística de Bolivia2.


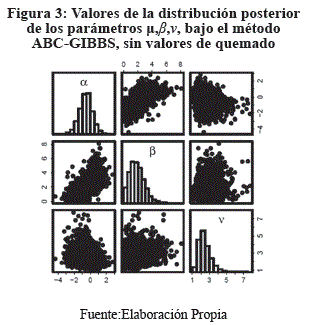
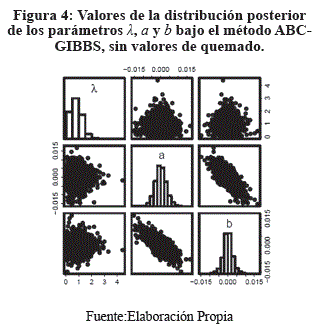
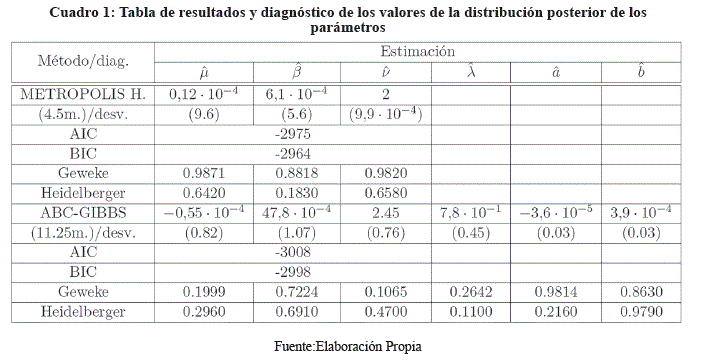
4. CONCLUSIÓN
Se aprecia que el método Metropolis Hastings presenta un menor tiempo de procesamiento en la estimación de los parámetros de la distribución de cambios de precios, sin embargo, el método ABCGIBBS presenta un mejor ajuste que el método Metropolis Hastings en los criterios AIC y BIC.
NOTAS
1 Los hiperparámetros son parámetros de una distribución previa
2 https://www.ine.gob.bo/index.php/serie-historicaempalmada/
BIBLIOGRAFÍA
1. Andrews, D., & Mallows, C. (1974). Scale mixtures of normal distributions. Journal of the Royal Statistical Society. Series B (Methodological), 36 (1), 99-102. Retrieved from http:// www.jstor.org/stable/2984774 [ Links ]
2. Barndoríf, O., & Blaesild, P. (1981). Hyperbolic Distributions and Ramifications: Contributions to Theory and Application (C. Taillie, G. P. Patil, & B. A. Baldessari, Eds.; pp. 19-44). Dordrecht: Springer Netherlands. doi: 10.1007/978-94-009-8549-0_2 [ Links ]
3. Barndoríf, O., & Halgreen, C. (1977). Infinite divisibility of the hyperbolic and generalized inverse Gaussian distributions. Zeitschrift Für Wahrscheinlichkeitstheorie Und Verwandte Gebiete, 38 (4), 309-311. doi: 10.1007/BF00533162 [ Links ]
4. Beaumont, M., Zhang, W., & Balding, D. (2002). Approximate Bayesian Computation in Population Genetics. Genetics, 162 (4), 2025-2035. [ Links ]
5. Blattberg, R., & Gonedes, N. (1974). A comparison of the stable and student distributions as statistical models for stock prices. The Journal of Business. [ Links ]
6. Diggle, P., & Gratton, R. (1984). Monte carlo methods of inference for implicit statistical models. Journal of the Royal Statistical Society. Series B (Methodological). [ Links ]
7. Gelman, A., Carlin, J. B., Stern, H. S., & B., R. D. (2013). Bayesian data analysis (A. C. P. Company, Ed.). Chapman & Hall/CRC Texts in Statistical Science. Retrieved from 24000/ e2cd08b709798adecf5e17aba6b1a033 [ Links ]
8. Grosswald, E. (1976). The student t-distribution of any degree of freedom is infinitely divisible. Zeitschrift Fur Wahrscheinlichkeitstheorie Und Verwandte Gebiete, 36 (2), 103-109. [ Links ]
9. Hastings, W. K. (1970). Monte carlo sampling methods using markov chains and their applications. Biometrika, 57 (1), 97-109. Retrieved from http://www.jstor.org/ stable/2334940 [ Links ]
10. Hichen, I., S.and Jerome. (2006). Bayesian blind separation of generalized hyperbolic processes in noisy and underdeterminate mixtures. IEEE Transactions on Signal Processing, 54 (9), 3257-3269. doi:10.1109/TSP.2006.877660 [ Links ]
11. Kyprianou, A. E. (2014). Fluctuations of Lévy Processes with Applications: Introductory Lectures (2nd ed.). Springer-Verlag Berlin Heidelberg. [ Links ]
12. Marjoram, P., Molitor, J., Plagnol, V., & Tavaré, S. (2003). Markov chain Monte Carlo without Likelihoods. Proceedings of the National Academy of Sciences, 100 (26), 15324-15328. [ Links ]
13. Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., & Teller, E. (1953). Equation of state calculations by fast computing machines. The Journal of Chemical Physics, 21 (6), 1087-1092. doi: 10.1063/1.1699114 [ Links ]
14. Ratmann, O., Andrieu, C., Wiuf, C., & Richardson, S. (2009). Model criticism based on likelihoodfree inference, with an application to protein network evolution. Proceedings of the National Academy of Sciences, 106 (26), 10576-10581. doi: 10.1073/pnas.0807882106 [ Links ]
15. Rosinski, J. (1991). On A Class of Infinitely Divisible Processes Represented as Mixtures of Gaussian Processes (S. Cambanis, G. Samorodnitsky, & M. S. Taqqu, Eds.; pp. 27-41). Boston, MA: Birkhauser Boston. doi: 10.1007/978-1-4684-6778-9_2 [ Links ]
16. Rubin, D. B. (1984). Bayesianly justifiable and relevant frequency calculations for the applied statistician. Ann. Statist., 12 (4), 1151-1172. doi:10.1214/aos/1176346785 [ Links ]
17. Sisson, S. A., Fan, Y., & Tanaka, M. M. (2007). Sequential monte carlo without likelihoods. Proceedings of the National Academy of Sciences, 104 (6), 1760-1765. doi:10.1073/ pnas.0607208104 [ Links ]
18. Tavare, S., Balding, D. J., Griffiths, R. C., & Donnelly, P. (1997). Inferring coalescence times from dna sequence data. Genetics. [ Links ]
19. Turner, B., & Sederberg, P. (2014). A generalized, likelihood-free method for posterior estimation. Psychonomic Bulletin Review, 21 (2), 227-250. doi: 10.3758/s13423-013-0530-0 [ Links ]
20. Turner, B., & Zandt, T. (2012). A tutorial on approximate bayesian computation. Journal of Mathematical Psychology, 56 (2), 69-85. doi: http://dx.doi.org/10.1016/j.jmp.2012.02.005 [ Links ]
21. Turner, B., & Zandt, V. (2014). Hierarchical Approximate Bayesian Computation. Psychometrika, 79(2), 185209. Retrievedfrom http://doi.org/10.1007/s11336-013-9381-x [ Links ]
22. Voss, J. (2013). An Introduction to Statistical Computing: A Simulation-based Approach (1sted.).Wiley. [ Links ]
 Citado por SciELO
Citado por SciELO
 Similares en SciELO
Similares en SciELO