ARTÍCULO DE INVESTIGACIÓN

 

La integral de Henstock - Kurzweil en la enseñanza de la teoría de la probabilidad

 

 

Lic. Esp. Delgado Álvarez, Raúl^1
1 Docente de la materia de Introducción a la teoría de la probabilidad de la Carrera de Estadistica de la Facultad de Ciencias Puras y Naturales de la UMSA.
dea_5@hotmail.com

 

 

---

Resumen

En el presente trabajo, se expone la relación entre la función de distribución acumuladay la función de probabilidades o la función de densidad de probabilidades de una variable aleatoria, a través de la integral de Henstock- Kurzweil, que se presenta como una generalización de la integral de Riemann, Riemann -Stieltjes y la de Lebesgue, esta relación se puede comprender mejor con el segundo teorema fundamental del Cálculo que tiene una interpretación más didáctica a través de la H-K integral, que también cumple con la rigurosidad requerida, para la comprensión y pruebas de los denominados teoremas de límites a través de los teoremas de la convergencia, la integral de H-K es de gran utilidad y comprensión como el Teorema de Convergencia Uniforme que se muestra en el presente trabajo.

Palabras Clave

Funciones de distribución, Integral de Henstock-Kurzweil, Segundo Teorema Fundamental del Cálculo, Convergencia Uniforme.

---

Abstract

In this paper, the relationship between the cumulative distribution function and the probability function or the probability density function of a random variable is exposed, through the Henstock-Kurzweil integral, which is presented as a generalization of the integral of Riemann, Riemann-Stieltjes and that of Lebesgue, this relationship can be better understood with the second fundamental theorem of Calculus that has a more didactic interpretation through the integral HK, which also meets the required rigor, for understanding and evidence of the so-called limit theorems through convergence theorems, the integral of HK is very useful and understanding as the uniform convergence theorem shown in the present work.

Keywords

Distribution functions, Henstock-Kurzweil Integral, Second Fundamental Calculation Theorem, Uniform Convergence

---

 

 

1. INTRODUCCIÓN

La relación existente entre la función de probabilidad o la densidad de probabilidades y la función de distribución acumulada se muestra frecuentemente en cursos regulares de teoría de la probabilidad, a través de un teorema de la Matemática denominado Teorema fundamental del Cálculo.

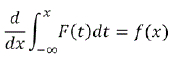
La relación enunciada se desarrolla en un curso inicial de Probabilidad, donde se hace mención de la Integral de Riemann, las limitaciones de la Integral de Riemann en la interpretación de funciones de distribuciones mixtas, es decir, discretas en un tramo y continuas en otro, en un curso de teoría de la Probabilidad intermedio o de introducción a la teoría de la probabilidad se salva esta interpretación a partir de la Integral de Riemann - Stieltjes:

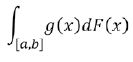
Que por supuesto, muestra una definición más consistente y general de la integración para tratar variables aleatorias mixtas, sin embargo, una condición para la existencia de la Integral de Riemann Stieltjes es el problema de la discontinuidad, es decir, cuando ambas funciones poseen puntos de discontinuidad en valores iguales, la función integrando en la Teoría de la Probabilidad generalmente es una función de la variable aleatoria como la función identidad en el caso de la esperanza matemática, funciones potenciales para explicar los momentos ordinarios o centrales y en general funciones que difícilmente poseen discontinuidades, en cambio la función integradora expresada por dF(x) es la que en caso discreto mostrará discontinuidades o saltos, por lo cual: la función F(x) debe ser de variación acotada esto es:

Esta dificultad nos hace pensar en la Integral de Lebesgue, pero es conocido que su tratamiento no es muy amigable por decirlo suavemente, entonces se debe reflexionar desde el inicio, es decir, cuando se habla por primera vez de la relación entre una función y su derivada.

La historia nos remonta al Siglo XVII con Isaac Newton que encontró que la integración es el proceso inverso de la derivación, es decir una función es newton integrable si tiene una anti derivada, posteriormente Agustin Cauchy define la integral de manera constructiva restringiendo a las funciones continuas, esta integral coincide con la integral de Newton, sin embargo debido a la existencia de derivadas no acotadas permanece más general la definición de Newton, luego Berhnard Riemann haciendo uso de puntos dentro de subintervalos, redefine la integral de Cauchy permitiendo la integración de algunas funciones discontinuas, es conocida esta integral por la sencillez para probar teoremas básicos y su manejo es el que se enseña en los cursos del Cálculo Diferencial e Integral hasta la actualidad pero existen algunas dificultades, para citar alguna es que la función de Riemann debe ser acotada y más aún la interpretación incompleta del Teorema Fundamental del Cálculo como proceso inverso al proceso de derivación hace desventajosa esta integral, posteriormente por el año 1902 aparece Henri Lebesgue que utiliza longitud de intervalos en su deducción, lo que supera las limitaciones de la integral de Riemann en cuanto a los teoremas de convergencia, la misma que es la más aceptada por la eficiencia de los mismos y la gran generalidad de funciones Lebesgue integrables, aún sin embargo existen funciones derivables en todo punto no necesariamente acotadas, cuya derivada F' no es Lebesgue integrable.

Mostrando una respuesta más satisfactoria al teorema fundamental del Cálculo, Denjoy y Perron definen una integral que permite recuperar a una función a partir de su derivada pero la definición de la misma es muy complicada, a continuación de este proceso en el año 1960 Ralph Henstock y Jaroslav Kurzweil formulan la H-K integral, que resulta un equivalente a la integral de Denjoy y Perron, pero dan una visión más general del Teorema Fundamental del Cálculo, es decir, una integración que retome la idea inicial de Newton.

Es así que relacionar a Newton y a Riemann parece importante por lo que la nueva integral debe ser más potente, y por supuesto la simplicidad de Riemann debe estar presente para recuperar una función f a partir de su derivada y sin imponer condición algún sobre F.

Se observa en la definición de la integral de Riemann, al dividir cada subintervalo no necesariamente tiene la misma longitud y más aún se escoge una etiqueta I de manera arbitraria (lo mismo puede estar al inicio como al final o en general, en un punto interior a cada subintervalo), por lo tanto la medida de fineza de una partición está dada por la máxima longitud de los subintervalos sin que dependan de las etiquetas, si se escogen subintervalos de menor longitud que cierta 5>0 significa que acota la norma de la partición en constante y por tanto los intervalos de la partición no siempre tienen una longitud adecuada, entonces es necesario considerar la relación entre las etiquetas y los intervalos para determinar la medida de fineza de la partición, así se observa en la integral de Henstock Kurzweil ilustrando como es que podemos recuperar una función F, a partir de su derivada F'.

A continuación, se expondrán los argumentos esenciales que en este trabajo son de mínima comprensión para definir la integral H-K, y se pondrá en evidencia la demostración del Segundo Teorema Fundamental del Cálculo y el Teorema de Convergencia Uniforme, pudiendo notar la sencillez de las indicadas pruebas a través de la integral de Henstock-Kurzweil.

 

2.- DESARROLLO

La descripción de la relación de cobertura, cubiertas de Cousin, el Teorema de Cousin son argumentos previos para la integral de Henstock-Kurzweil, y los teroremas: II Teorema del Cálculo y el Teorema de la Convergencia Uniforme muestran la potencia de la integral H-K.

Relación de cobertura.- Es una familia de parejas ([c,d], x), donde x e [c,d].

Sea F'(x)=f(x) para toda x e [a.b], sea ε>0, consideremos la relación de cobertura β que consiste en todos los pares de intervalos y puntos ([c,d], t) para los cuales ε[c,d] con [c,d]⊂ [a,b] con la propiedad de que , obsérvese que la relación de cobertura es muy grande, ya que por definición de diferenciabilidad, para cada punto t ε[a,b] existe un δ_t> 0 tal que β contiene a todas las parejas ([c,d], t) con d-c < δ_t.

Supóngase que β contiene una partición: , la diferenciaF(b) -F(a) como la suma telescópica:

por lo tanto se obtiene:

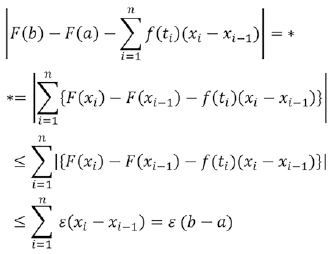
Se concluye entonces que

Esto indica que la integral puede ser aproximada por la suma de Riemann, pero seleccionando las etiquetas t de una manera distinta a como procede en el contexto de Riemann, es decir se ha utilizado una partición cuyos elementos provienen de

una relación de cobertura que describa de manera natural la geometría del problema es decir, partiendo de la diferenciabilidad de la integral indefinida F.

Cubiertas de Pierre Cousin

Una relación de cobertura β es una cubierta de Cousin de un intervalo [a, b] si para cada xε[a,b], existe δ>0 tal que β contiene todos los pares ([c,d], x), para los cuales xε[c,d] ⊂[a,b] y (d-c) < δ.

Sea β una cubierta de Cousin del intervalo [a,b], entonces β es una cubierta de Cousin de cada subintervalo [c,d] ⊂ a,b]. Esto quiere decir que si xε[c,d]⊂[a,b]. Como xε[a,b] entonces existe δ>0 tal que β contiene a todos los pares (I,x) con xεI⊂[a,b] y I(I)<δ. Si el par (J,x) es tal que xεJ⊂[c,d] con l(J)<δ, entonces (J,x) debe estar en β ya que J⊂ [a, b].

Al considerar dos cubiertas de Cousin para comprobar que la intersección es también una cubierta de Cousin sobre el intervalo [a,b], será suficiente considerar: δ = min{δ_p δ₂}

Teorema de Cousin

Sea δ un indicador en [a,b], entonces existe una partición δ - fina de [a,b].

Demostración: Por el método del absurdo reducción al absurdo.

Supóngase que [a,b] no tiene partición δ -fina.

Sea y considérense los subintervalos [a,c] y [c,b], si los dos [a,c] y [c,b] intervalos tuviesen una partición δ-fina entonces su unión será una partición δ-fina de [a,b], es decir, alguno de los subintervalos [a,c] y [c,b] no tiene partición δ-fina, sin perdida de generalidad será I’=[a1,b1], sea y considérese los subintervalos [a1,c1] y [c1,b1] y uno de los intervalos no tiene partición δ-fina, sea I²=[a₂,b₂] este subintervalo, así deestamanera, se obtiene una sucesión de intervalos compactos encajados {Iⁿ}_nεN uno con longitud sin partición δ-finas, luego por el teorema de los intervalos encajados se asegura que existe un único punto x en la intersección de todos los intervalos Iⁿ sin embargo como δ(x)>0 por la propiedad Arquimediana existe pεN tal que por tanto

Además el par {(I^p,x)} es una partición formada por un solo intervalo δ-fina de I^p en contra de la elección de I^p.

Esta contradicción prueba que [a,b] tiene alguna partición δ-fina, como se quería probar.

Definición de la HK-integral

Una función f:[a,b]—>IR es HK integrable sobre un intervalo [a,b] si existe un número A tal que para cada ε>0, podemos encontrar una cubierta de Cousin β de [a,b] con la propiedad de que para cada partición π contenida en β

Generalmente, se encuentra la definición de HK-integral utilizando funciones positivas δ:[a,b]—>(0,∞), Conocidas como gauges, si π ={([u_i,v_i],t_i):i=1,2,.....n} es una partición etiquetada de [a,b] entonces se dice que π es δ-fina si t_iε[u_i ,v_i]⊂[t_i-δ(t_i),t_i+δ(t_i)] de esta manera el Lema de Cousin tiene un equivalente para un gauge, es decir, si δ:[a,b]—>(0,∞) es un gauge y si a≤c≤d≤ b existe una partición δ-fina de [c,d]. Se dice quef:[a,b]—>IR es HK- integrable si existe un A e IR tal que para cada ε > 0, existe un gauge δ con propiedad de que si π es una partición δ-fina, entonces se verifica, sin embargo esta definición es equivalente a aquella en la cual se utilizan integrales superiores e inferiores.

Dada por fija una cubierta de Cousin β , la suma inferior L(f,β) y la suma superior S(f,β) de una función f definida sobre [a,b] están dadas por

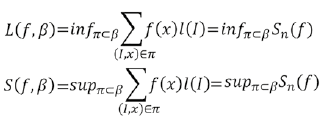
Donde el ínfimo y el supremo se toman sobre todas las particiones en β.

Sea f una función real definida sobre [a,b], se define la integral inferior I_ como:

Donde el supremo se toma sobre todas las cubiertas de Cousin de [a,b], análogamente definimos la integral superior como el ínfimo de las sumas superiores

Cuando , se tiene el valor común como si además este valor es finito, decimos que fes integrable, se observa que

Al considerar dos cubiertas de Cousin P_p fí₂ de [a,b], tales que β_1,β₂ cualquier partición en β₁es una partición en β₂, pero el recíproco no es necesariamente cierto, por lo cual ,similarmente , por lo cual se puede concluir que:

cada suma inferior es menor o igual a cada suma superior.

Si β es una cubierta de Cousin arbitraria, como: S(f,β) es cota superior para todas las sumas inferiores, y I es la mínima cota superior de las sumas inferiores, entonces I ≤ S(f,β).

Dado que β es arbitrario, entonces I es cota inferior para todas las sumas superiores y como I es la máxima cota inferior de las sumas superiores se sigue que , por lo tanto:para toda cubierta de Cousin β.

El Segundo Teorema Fundamental del Cálculo, IITFC

Lema. Sea F:[a,b]—Runa función derivable en t ε[a,b] dado ε > 0, existe δ_e(t) > 0 tal que si c,dε[a,b] satisfacen: t-δ_e(t) ≤c ≤t ≤d ≤ i+δ_e(t) entonces:

|F(d) - F(c) - F '(t) (d-c)\≤ε(d-c)

Definición.

Sea F:[a,b]→R una función derivable en [a,b] entonces, F' es integrable en el sentido de Henstock-Kurzwiel en [a,b] y además , para cada xε[a,b].

Prueba. Para x = b, sea ε > 0 considérese el indicador asociado a , por el lema anterior. Sea una partición

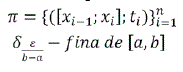
de ahí se probará que |F(b)-F(a)-S(F ',π)| ≤ ε. Como para cada i ε{1,2,...,n}; x_i-1 y x_i verifican: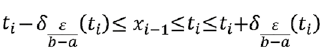

Por la propiedad enunciada en el lema anterior se tiene que para cada i ε {1,2,...,n},

Para estimar F(b) - F(a) - S(F’,π) se utiliza la suma telescópica

De modo que:

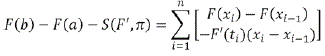
entonces:

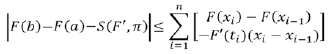
se tiene:

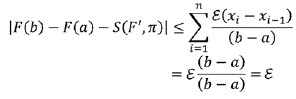
En el estudio de la integral de Riemann, el limite f de una sucesión {f_n} de funciones Riemann integrables no es necesariamente Riemann integrable incluso el limite fuese Riemann integrable, es decir, su integral podría diferir del límite de una sucesión. El intercambio de operaciones:

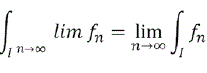
Es posible si la sucesión {f_n} converge uniformemente, pero esta condición es fuerte.

Una de las principales razones por las que la integral de Lebesgue se convertido en una herramienta central e indispensable del Análisis Matemático es por sus teoremas de convergencia la integral de Lebesgue ha remediado eficientemente el problema de asegurar la igualdad enunciada requiriendo hipótesis no tan fuertes.

El mismo tratamiento para la integral de Henstock-Kurzweil también se cumple, pero su explicación es más didáctica.

El Teorema de Convergencia Uniforme

La condición que garantiza la integrabilidad de una función limite y el intercambio citado concerniente a la noción de convergencia uniforme se sigue cumpliendo para la HK-integral.

Definición: una sucesión {f_k} de funciones reales definidas sobre un intervalo cerrado I converge uniformemente sobre I a una función f si para cada ε > 0 existe N ε N tal que

Teorema Convergencia Uniforme:

Si la sucesión {f_n}⊂HK(I) converge uniformemente a f entonces fεTK(I) y la igualdad de intercambio se verifica.

Demostración:

Primero se probará que {f₁f_n} es una sucesión de Cauchy, Dado ε> 0, por la definición de convergencia uniforme de la sucesion {f_n},existe N ε N tal que si h, k > N y xεI entonces

Por la monotonía y la linealidad de la integral, tenemos que como ε > 0 es arbitrario la sucesion {∫_If_n}es la Cauchy y por lo tanto converge a un número real AεR

Se mostrará entonces que f ε HK(I) y que A es su integral .Sea ε > 0 y N sea k ≥ N fijo tal que Ahora sea β una cubierta de Cousin, de la definición de integrabilidad de f_k, de manera que siempre que π ⊂ tenemos que por la convergencia uniforme

 

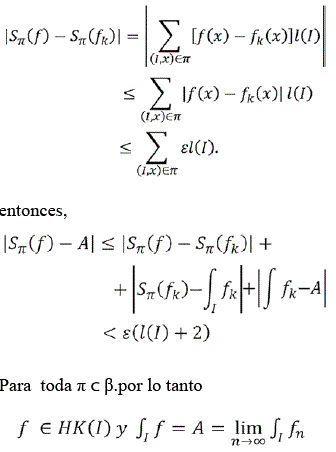
3.- RESULTADOS

La relación entre las funciones de distribución y la de densidad de probabilidades, se puede enunciar desde la Integral de Riemann Stieltjes bajo la condición de que el integrando sea una función continua en todo su dominio y el integrador una función de variación acotada esto es

El estudio de los teoremas de convergencia son tratados de manera más didáctica con la integral de Henstock-Kurzweil, así evitar el tratamiento riguroso de la integral de Lebesgue, como se mostró en la prueba del Segundo Teorema Fundamental del Cálculo y el Teorema de Convergencia Uniforme sin recurrir a la teoría de la medida, es mas a partir de la integral de Henstock-Kurzweil puede definirse la teoría de la medida y la integral de Lebesgue en los Reales, como lo proponen Gordon Russell en The integral of Lebesgue, Denjoy, Perron and Henstock 1944 y Robert Bartle en A modern theory of integration 2001,

 

4.- CONCLUSIONES

La relación expresada en el Teorema Fundamental del Cálculo, muestra de manera didáctica pero formal, la relación entre la función de distribución acumulada y la función de probabilidad a través de la integral de Henstock-Kurzweil, donde las reglas desarrolladas para calcular integrales son válidas , además no existen integrales impropias en el sentido de H-K , es decir, si podemos definir la integral de Henstock-Kurzweil de una función como el límite de unas integrales de la función en su intervalos del dominio, entonces la función es inmediatamente integrable en el sentido de Henstock-Kurzweil en todo el intervalo, así se puede notar que la integral de Henstock Kurzweil es estrictamente más general que las integrales de Riemann y Lebesgue .

A diferencia de la integral de Riemann y la de Lebesgue, el Teorema Fundamental del Cálculo, garantiza que la derivada de cualquier función sobre un intervalo I, siempre es H-K integrable.

La enseñanza de la Teoría de la Probabilidad a nivel intermedio o superiores, debería incluir un estudio del Cálculo Diferencial e integral incluyendo la Integral de Henstock-Kurzweil para poder contar con un instrumento Matemático general y riguroso para el estudio de los teoremas límites en el análisis de la convergencia y comprender mejor los teoremas límites de la teoría de la

Probabilidad, por lo cual la recomendación de muchos autores reconocidos como Robert Bartle de Estados Unidos, Ralph Henstock de Irlanda, Jaroslav Kurzweil Republica Checa Rudolf Výrborný de Australia, Eric Schechter de Estados Unidos, Stefan Schwabick de la Republica Checa abogan por la inclusión en los libros de Cálculo, la Intgral de Henstock-Kurzweil argumentando que algunas definiciones y teoremas se pueden indicar de manera más simple y más fuertes si se utiliza la Integral de Henstock -Kurzweil.

En el estudio de la teoría de la Probabilidad no solo nos permite tratar de manera unificada la definición de integral, para la comprensión de los conceptos de las características numéricas como el valor esperado, varianza, momentos, etc. Si no también como se pudo observar en los anteriores teoremas serian de gran ayuda para la comprensión de los Teoremas límites de la teoría de la probabilidad, de esta manera el estudio del Cálculo integral debería incluir la integral de Henstock-Kurzweil en el pensum para los estudiantes de una Carrera de Ciencias.

 

BIBLIOGRAFÍA

Robert Bartle, (2001), "A modern Theory of integration, Graduate studies in Mathematics".        [ Links ]

Javier Herrera, (2005) Tesis: "La integral de Henstock-Kurzweil”.        [ Links ]

Adriana Ocej o Monge, (2008) "La integral de Henstock-Kurzweily el Teorema fundamental del Cálculo".        [ Links ]

Javier Martínez Perales,(2017), "La integral de Henstock Kurzweil y el segundo Teorema del Cálculo".        [ Links ]

Luis Rincón, (2007), "Curso intermedio de Probabilidad”, Facultad de Ciencias UNAM.        [ Links ]