ARTICULOS

 

Estimación Bayesiana de los Resultados de las Encuestas Electorales

 

 

Lic. Dindo Valdez Blanco
dindovaldez@hotmail.com

 

 

---

Resumen. En el presente artículo se revisan los elementos básicos del paradigma bayesiano y se realiza una estimación bayesiana puntual y de intervalo de la proporción de votación a favor del actual presidente Evo Morales basado en los resultados de la encuesta realizada por la empresa Ipsos en el mes de agosto de 2014.

Palabras clave: Inferencia Bayesiana, encuestas electorales, función a priori, función a posteriori.

---

 

 

1.    Introducción

El presidente del Estado Evo Morales, domina con amplia ventaja en las encuestas seis semanas antes de las elecciones generales del 12 de octubre. En la encuesta realizada por la encuestadora privada Ipsos, Morales se encuentra a la cabeza de intención electoral con un caudal del 59 %, y 42 % de voto seguro. La ficha técnica de dicho sondeo indica que se entrevistó a 3000 ciudadanos entre el 1 y 16 de agosto, la muestra tiene una confianza de 95 % y un error máximo de estimación de 1.79 %, la encuesta fue efectuada en 10 ciudades capitales, 10 localidades urbanas y 88 localidades rurales de Bolivia.

Estos resultados son estimaciones del tipo frecuentista denominado estimación clásica, sin embargo es posible obtener una estimación bayesiana y calcular la precisión que tienen ambos estimadores.

 

2.    El paradigma bayesiano

Si definimos el parámetro como la proporción de electores de la población que tienen la intención de votar por Evo Morales, definimos también una variable binaria X, tal que x = 0 si una persona no piensa votar por el actual presidente, y x = 1 si tiene la intención de votar por el candidato oficialista. Entonces la función de probabilidad de X condicionada en el parámetro es Bernoulli, tal que su función de probabilidad paramétrica es:

El estimador máximo verosímil de basado en una muestra aleatoria de tamaño n de X está definido por: , el mismo basado en los datos de la encuesta electoral resulta igual a = 0.59. En este caso se considera a como un parámetro desconocido pero fijo.

Sin embargo desde el punto de vista bayesiano, el parámetro es una variable aleatoria. Este aspecto tiene sentido porque la intención de voto de los electores es cambiante, debido a muchos factores como la información que emiten los medios de comunicación y las propuestas de los candidatos. La estima ción bayesiana se basa en la función de probabilidad condicional denominada función de probabilidad a posteriori definida por:

 

3. Estimación bayesiana tomando una función a priori Beta

Si se supone una función a priori Beta(,) para con y conocidos:

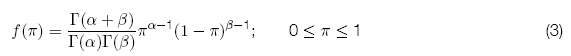
La función de probabilidad a posteriori de dada la información de la muestra resulta:

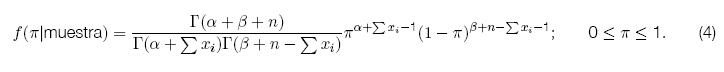
Claramente se reconoce que la distribución posterior corresponde a una ley . Basado en este hecho el estimador de Bayes se define como la media condicional de la función posterior:

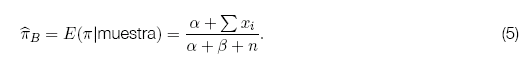
Para la elección de los valores iniciales y , se puede utilizar un sistema de ecuaciones basados en la media y varianza de la distribución a priori de , si se considera una media igual a 0.5 y una varianza de 0.01, el sistema resulta:

De donde se obtienen los valores iniciales = 12, = 12. Tomando la información de la muestra n = 3000, = 1770, el estimador bayesiano resulta = 0.5893. De la misma manera se puede calcular un intervalo de confianza al 95% para la estimación bayesiana basado en los percentiles 2.5 y 97.5 de la distribución . De donde resulta el intervalo (0.5717; 0.6068).

 

4. Estimación bayesiana tomando una función a priori Uniforme

Si no se tiene ninguna suposición sobre la distribución del parámetro se puede asumir una función de probabilidad uniforme U(0,1), es decir: f() = 1,0 1. De igual manera se obtiene la función de densidad posterior de dada la información de la muestra:

La expresión anterior muestra que la distribución a posteriori también sigue una ley . Nuevamente reemplazando las observaciones de la muestra, se tiene que la distribución a posteriori es |muestra ~ . Por tal razón el estimador puntual bayesiano de la proporción de la población que piensa apoyar al presidente en las próximas elecciones es igual a la media condicional de la densidad posterior.

Finalmente el intervalo de confianza al 95 % para el parámetro desde el enfoque bayesiano es (0.5626; 0.5976).

 

5. Medida de precisión de los estimadores

El estimador frecuentista clásico es insesgado, en cambio los estimadores bayesianos por lo general tienen un sesgo, la diferencia radica en que el Error Cuadrático Medio de las estimaciones es menor en el caso Bayesiano en comparación del estimador frecuentista. El error cuadrático medio (ECM) de un estimador está definido como:

En el caso del estimador frecuentista t?f,su media y varianza son: . Por lo que su ECM resulta:

Con n = 3000 y = 0.5, se tiene un error cuadrático medio igual a . De igual manera para el caso bayesiano la media y varianza de es igual a:

De tal forma que su error cuadrático medio es igual a:

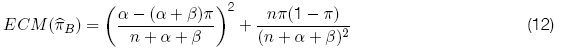
Con n = 3000, = 0.5, = 12 y = 12, se obtiene . Esto confirma que el estimador bayesiano tiene menor error en comparación con el estimador frecuentista.

La siguiente tabla muestra las estimaciones del parámetro con sus respectivos intervalos de confianza.

 

6. Conclusión

Mediante esta aplicación se concluye que los estimadores bayesianos tienen igual o mejor precisión que el estimador frecuentista, adicionalmente la estimación bayesiana es muy parecida en los dos casos, no importando la función a priori inicial que se tome.

 

Referencias

[1] Bernardo, J. M., Bayarri, M. J., Berger, Bayesian Statistics. Oxford: University Press, 2003.        [ Links ]

[2] Lee, P. M. Bayesian Statistics: An Introduction (3rd. ed.) London University Press, 2004.        [ Links ]