ARTÍCULOS

 

Algoritmo de Fortune sin eventos de círculo usando la primitiva InCircle

 

Fortune 's algorithm without circle events using InCircle primitive

 

 

Lucio Torrico
Instituto de Investigaciones en Informática Carrera de Informática
Facultad de Ciencias Puras y Naturales Universidad Mayor de San Andrés
La Paz - Bolivia
Autor de correspondencia: luciotorrico@informatica.edu.bo
Presentado: La Paz, 25 de octubre de 2016 Aceptado: La Paz, 20 de Diciembre de 2016

 

 

---

Resumen

Para hallar el diagrama de Voronoi (también llamado teselación de Dirichlet o polígonos de Thiessen) de un conjunto de puntos en el plano, el algoritmo de Fortune usa la propiedad de círculo vacío alrededor de los vértices de un modo implícito.

Todas las presentaciones de dicho algoritmo usan eventos de círculo sin cálculos explícitos de la primitiva InCircle.

El objetivo es averiguar si existe una versión alterna del algoritmo de Fortune sin eventos de círculo, utilizando exhaustivamente la primitiva InCircle.

Se ha diseñado dicha variante del algoritmo, argumentado sus basamentos y, además de la presentación, se incluye un ejemplo de ejecución que permite aclarar su uso.

Palabras clave: algoritmo de Fortune; diagrama de Voronoi., primitiva InCircle

---

Abstract

To find the Voronoi diagram (also called Dirich let tessellation or Thiessen polygons) from a set of points in the plane, Fortune 's algorithm use the empty-circle property around the vertices in an implicit way.

All presentations of this algorithm use circle-events without explicit calculations of the primitive InCircle.

Our goal is to find out if there is an alternate version of Fortune 's algorithm without circle-events, using exhaustively the primitive InCircle.

We have designed this variant of the algorithm, argued their bases and, in addition to the presentation, include an execution example that allows clarify their use.

Keywords: Fortune 's algorithm; InCircle primitive; Voronoi diagram

---

 

 

Introducción

Desde que (Guibas, L. 1, Stolfi, J., 1989) dieron una nueva presentación al algoritmo de Fortune (Fortune, 1987) para el cálculo del diagrama de Voronoi de un conjunto C de sitios o puntos en 2D, dicha presentación se ha popularizado hasta convertirse prácticamente en un estándar (De Berg et al. 1997, O'Rourke 1994).

Aquí se presenta otra forma de calcular el diagrama, basados en dicho algoritmo pero sin utilizar eventos de círculo.

La versión estándar que se relata, utiliza los llamados eventos de círculo de manera explícita y exhaustiva a partir de tripletas en la línea de playa, calculando el circuncentro de la circunferencia definida por los sitios de la tripleta, y luego restando el radio (previamente calculado) para hallar el punto más bajo de dicha circunferencia.

En su lugar se calcula la primitiva InCircle para ver si un sitio está dentro del círculo definido por los tres sitios de una tripleta, de ser así la tripleta no es más que una falsa alarma. Si el sitio está fuera, o lo trabaja como un sitio más añadiéndolo a la línea de playa, o si está fuera y muy abajo se concluye que la circunferencia está vacía y define un vértice.

 

Primitiva InCircle

Dada una tripleta de puntos p₁ p₂ p₃ no colineales (que en ese orden están en sentido antihorario), un nuevo punto p4 está dentro del círculo definido por la tripleta cuando:

Lo que se conoce como la primitiva InCircle (p₁,p₂, p₃,p₄ ) (Gravesen 2012).

 

Evento de sitio

Cuando un sitio nuevo está en la punta de la cola, debe manejarse: corta a un arco, define tripletas, etc.

Si está dentro del círculo de una tripleta previamente definida, dicha tripleta convergente es una falsa alarma, pues es una propiedad conocida (De Berg et al., 1997) que los vértices de un diagrama de Voronoi son el centro de círculos vacíos que tienen en el borde de su circunferencia tres (o más) sitios.

 

La variante

Para el cálculo del diagrama de Voronoi, no se maneja eventos de círculo, sólo eventos de sitio.

La cola de prioridad Q contienen los sitios clasificados de mayor a menor de acuerdo a su ordenada. La lista doblemente enlazada D alberga las aristas y los vértices.

Seguir manejando el concepto de tripleta, aunque los arcos centrales no apuntarán a nada en Q. Sí tendrán un indicador de que son centros de tripleta en caso de convergencia.

Al bajar la línea de barrido: para determinar el nodo hoja que se corta, el orden de los subíndices de un nodo intermedio en el árbol T, importa:

1) menor,MAYOR (por ej, <p₁ p₃>): representa una intersección izquierda (*)

2) MAYOR,menor (por ej, < p₃ p₂>): representa una intersección derecha

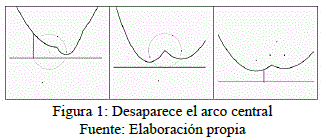
La variante se basa en el siguiente hecho: una tripleta convergente en el algoritmo estándar define un círculo, el arco central desaparece al llegar al circle-event añadiendo un vértice. Para el siguiente sitio ese arco ya no juega ningún rol (pues en dicho algoritmo estándar, se elimina). Ver un ejemplo en la Figura 1.

Como no se tiene eventos de círculo, se debe identificar cuándo ha sobrepasado ese ficticio punto extremo de las ficticias circunferencias. Se explica con un ejemplo básico, pero generalizable: la línea de playa tiene este desarrollo (sin eventos de círculo). Luego de los tres primeros sitios:

Se ha marcado el sitio que desaparecería en el ficticio evento de círculo.

Cuando aparece p₄, cortará a p₃. El vecino derecho de p₃ es p₁ que tiene un indicador de que es centro de tripleta.

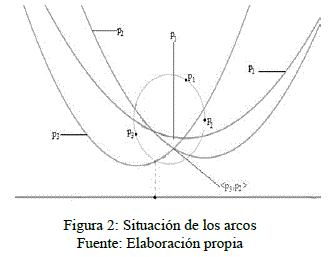
Nótese que cuando el nuevo sitio está fuera de la circunferencia ficticia, el arco de parábola que debía desaparecer, señalado con una línea vertical correspondiente a p₁, es tal que la situación de los arcos viene graficada según lo muestra la siguiente figura 2:

Si calcula la abscisa de la intersección entre los extremos de p₃ p₁ p₂, es decir <p₃,p₂>, la ordenada de dicha intersección está más abajo que la ordenada del arco de parábola p₁calculada en dicha abscisa.

Ese será el dato que se necesita para eliminar p₁.

Es interesante anotar que la abscisa de la intersección puede calcularse sin utilizar raíz cuadrada (sqrt).

Este es un ejemplo genérico, puede verse la misma situación en cualquier momento en que procesa los sitios de la cola, no sólo con los cuatro primeros sitios:

Los arcos que deben desaparecer, lo que era notorio en los eventos de círculo, ahora salen a la luz cuando están por encima de intersecciones.

Si un sitio nuevo cae dentro de una circunferencia, se eliminan la falsa alarma.

Si está fuera de la circunferencia:

• Es posible que esté por encima de la ficticia línea horizontal donde estaría el evento de círculo -ahora inexistente-, en cuyo caso debe tratarse como un sitio más.

• Es posible que esté debajo de dicha línea ficticia, en cuyo caso, dado que los sitios se trabajan en orden, la circunferencia define un vértice (eso se puede reconocer según lo dicho con ayuda de la Figura 2); entonces se define el vértice, desaparecen arcos y luego se trata el sitio como antes.

Debido a que no hay eventos de círculo, pueden existir iteraciones.

 

Métodos

Además de recurrir a la recopilación documental y su selección, principalmente se ha utilizado el método analítico deductivo y, dentro de él, esquemas usuales de demostración, técnicas de diseño de algoritmos, en particular los de barrido, así como técnicas de análisis de algoritmos, en particular los que conciernen a la complejidad temporal.

 

Resultados

El principal resultado es la construcción de la variante del algoritmo de Fortune sin eventos de círculo. Se muestra completo en la página siguiente.

En el Anexo se presenta un ejemplo de ejecución de la variante, mismo que termina de clarificar algunas partes.

 

Discusión

La variante presentada sigue perteneciendo a la clase de algoritmos de barrido y, al estar basado en el algoritmo de Fortune su complejidad temporal es 0(n log n).

Aunque ya no hay eventos de círculo, los arcos se añaden a la línea de playa o desaparecen de él iterativamente, en las estructuras "Mientras" del algoritmo.

 

Conclusiones

Se ha mostrado que con la ayuda de la primitiva InCircle explícitamente utilizada, puede construirse una alternativa de presentación del algoritmo de Fortune popularizado por (Guibas L. J., Stolfi J., 1989).

A diferencia de dicho estándar, la alternativa que se presenta no tiene eventos de círculo.

El ejemplo de ejecución (que puede verse en el Anexo) muestra operativamente la teoría de base y el algoritmo propiamente dicho en acción.

Tener una variante de cualquier algoritmo es muy común en Ciencias de la Computación, y pueden buscarse ventajas y beneficios de ella.

 

Agradecimientos

Un agradecimiento especial a los estudiantes que colaboraron temporalmente con este trabajo: Rodrigo Castillo, Gauss Carvajal, Fernando Tórrez, Leonardo Ríos y Adrián Fernández.

 

Referencias

De Berg, M., Van Kreveld, M., Overmars M., Scwarzkopf, O. (1997). "Computational geometry ". Springer.        [ Links ]

Fortune, S. (1987). "A Sweep Une Algorithm for Voronoi Diagrams", Algorithmic, pp. 153-174.        [ Links ]

Gravesen, J. (2012). "Guide to Computational Geometry Processing". Springer.        [ Links ]

Guibas, L. J, Stolfi J. (1989). "Ruler, Compass, and Computer: The Design and Analysis of. Geometric Algorithms". En "Theoretical Foundations of Comput. Graph. and CAD", Vol. 40, pp. 111-165. Springer.        [ Links ]

O'Rourke, C. J. (1994). "Computational geometry". Cambridge University Press.        [ Links ]

 

ANEXO

Para el primer y segundo sitios se coloca p₁ p₂ p₁ en la linea de playa. Se añade la arista p₁-p₂ a D.

Para cada siguiente sitio nuevo p_k en la cola de prioridad Q:

Sea p₁ el sitio cortado por p_k. Vemos si el arco cortado, su predecesor o su sucesor tienen un indicador de centro de tripleta convergente. Para cada uno de ellos:

1)   Mientras el predecesor del arco cortado tiene indicador de tripleta

AND

el nuevo sitio est á fuera de la circunferencia definida por los tres sitios

AND

la ordenada de la intersección de las parábolas de los costados (tomándolos en el orden señalado en (*))

es menor que (<) (en nuestro contexto está más abajo)

la ordenada de la parábola del predecesor considerado evaluada en la abscisa de dicha intersección :

La tripleta define un vértice: insertar vértice. Añadir arista con los extremos de la tripleta. Eliminar el sitio (arco) central a de la tripleta En la nueva linea de playa,
verificar tripletas involucradas con el sitio eliminado, llamémoslo p_j:

Si predecesor de p_j tomado como centro de tripleta converge: añadir indicador Si sucesor de p_j tomado como centro de tripleta converge: añadir indicador

Fin-Mientras

Si el predecesor del arco cortado tiene indicador de tripleta

AND

el nuevo sitio está dentro de la circunferencia definida por la tripleta:

borrar indicador (falsa alarma)

2)   Mientras el sucesor del arco cortado tiene indicador de tripleta

AND

el nuevo sitio está fuera de la circunferencia definida por los tres sitios

AND

la ordenada de la intersección de las parábolas de los costados (tomándolos en el orden señalado en (*))

es menor que (<) (en nuestro contexto está más abajo)

la ordenada de la parábola del predecesor considerado evaluada en la abscisa de dicha intersección :

La tripleta define un vértice: insertar vértice. Añadir arista con los extremos de la tripleta. Eliminar el sitio (arco) central a de la tripleta En la nueva linea de playa,

verificar tripletas involucradas con el sitioeliminado, llamémosmlo p_j:

Si predecesor de p_j tomado como centro de tripleta converge: añadir indicador

Si sucesor de p_j tomado como centro de tripleta converge: añadir indicador

Fin-Mientras

Si el sucesor del arco cortado tiene indicador de tripleta

AND

el nuevo sitio está dentro de la circunferencia definida por la tripleta:

borrar indicador (falsa alarma)

3) Si el arco cortado tiene indicador de tripleta:

Si el nuevo sitio está dentro de la circunferencia definida por los tres sitios correspondientes a la tripleta: borrar indicador (falsa alarma).

Insertar arista p_k-p_i.

Insertar p_k que (corta p_i) en la linea de playa.

Verificar tripletas (p_k el más izquierdo/derecho): si converge añadir indicador.

Terminación: (ya acabamos con todos los sitios p_k, cola de prioridad Q vacia) Es posible que la linea de playa contenga sitios con indicador de tripleta:

Mientras haya sitios con indicador de tripleta
La tripleta define un vértice, añadirlo.
Añadir arista con los extremos de la tripleta.
Eliminar el sitio (arco) central α
En la nueva linea de playa,

verificar tripletas involucradas con el sitioeliminado, llamémosmlo p_j:
Si predecesor de p_j tomado como centro de tripleta converge: añadir indicador

Si sucesor de p_j tomado como centro de tripleta converge: añadir indicador
Fin-Mientras

EJEMPLO DE EJECUCIÓN DE LA VARIANTE

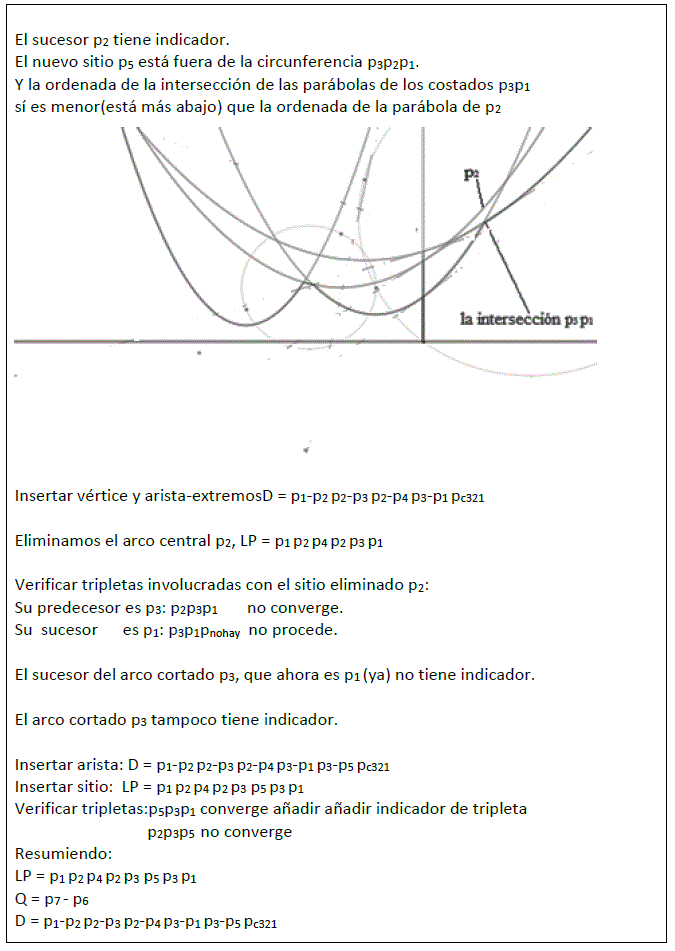
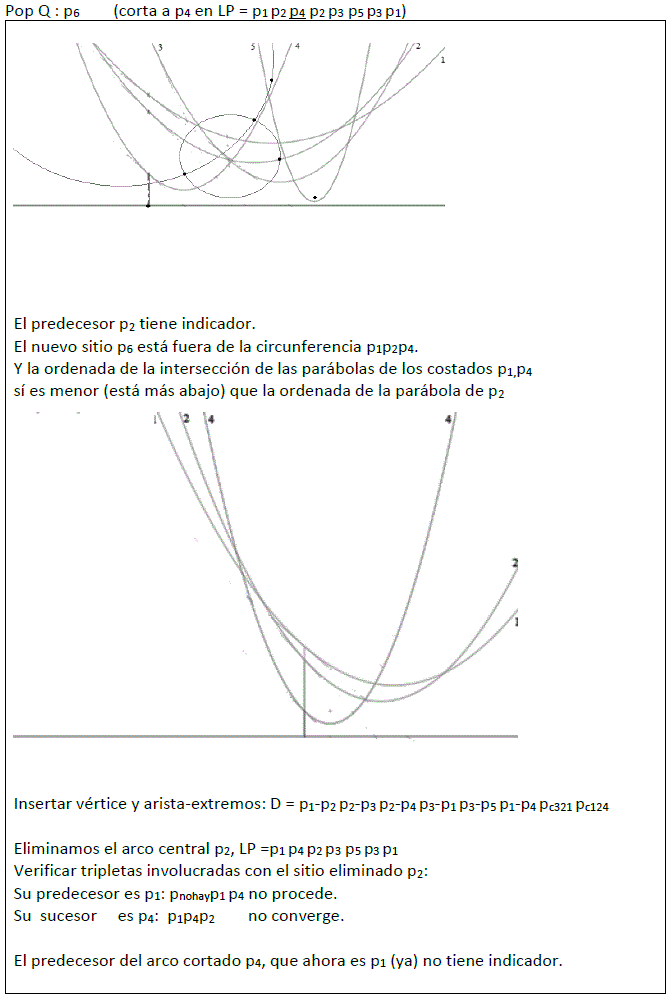
Terminación:

La cola está vacía pero la línea de playa contiene sitios con indicador de tripleta.

LP = p₁ p₄ p₆ p₄ p₇ p₄ p₃ p₅ p₃ p₁

Insertar vértice y arista-extremos para p₁ p₄ p₆:

D = p₁-p₂ p₂-p₃ p₂-p₄ p₃-p₁ p₃-p₅ p₁-p₄ p₄-p₃ p₄-p₆ p₄-p₇ p₁-p₆ p_c321 p_c124 p_c423 p_c146

Eliminar arco central p₄:

LP =p₆ p₆ p₄ p₇ p₄ p₃ p₅ p₃ p₁

Verificar (en la nueva línea de playa) tripletas involucradas con el sitio eliminado p₄:
Su predecesor es p₁: p_nphayp₁p₆ no procede.
Su sucesor es p₆:p₁p₆p₄ no converge.

Insertar vértice y arista-extremos para p₆ p₄ p₇:

D = p₁-p₂ p₂-p₃ p₂-p₄ p₃-p₁ p₃-p₅ p₁-p₄ p₄-p₃ p₄-p₆ p₄-p₇ p₁-p₆ p₆-p₇ p_c321 p_c124 p_c423 p_c146 p_c647

Eliminar arco central p₄:

LP = p₁p₆p₇p₄p₃ p₅p₃p₁

Verificar (en la nueva línea de playa) tripletas involucradas con el sitio eliminado p₄:
Su predecesor es p₆: p₁p₆p₇ no converge.
Su sucesor es p₇: p₆p₇p₄ no converge.

Insertar vértice y arista-extremos para p₇p₄p₃:

D = p₁-p₂ p₂-p₃ p₂-p₄ p₃-p₁ p₃-p₅ p₁-p₄ p₄-p₃ p₄-p₆ p₄-p₇ p₁-p₆ p₆-p₇ p₇-p₃
p_c321 p_c124 p_c423 p_c146 p_c647 p_c743

Eliminar arco central p₄:

LP = p₁p₆p₇p₃ p₅p₃p₁

Verificar (en la nueva línea de playa) tripletas involucradas con el sitio eliminado p₄:

Su predecesor es p₇: p₆p₇p₃ no converge.
Su sucesor es p₃: p₇p₃p₅ converge, añadir indicador de tripleta.

LP = p₁p₆p₇p₃ p₅p₃p₁

Insertar vértice y arista-extremos para p₇p₃p₅:

D = p₁-p₂ p₂-p₃ p₂-p₄ p₃-p₁ p₃-p₅ p₁-p₄ p₄-p₃ p₄-p₆ p₄-p₇ p₁-p₆ p₆-p₇ p₇-p₃ p₇-p₅
p_c321 p_c124 p_c423 p_c146 p_c647 p_c743 p_c735

Eliminar arco central p₃:

LP = p₁p₆p₇p₅p₃p₁

Verificar (en la nueva línea de playa) tripletas involucradas con el sitio eliminado p₄:
Su predecesor es p₇: p₆p₇p₅ no converge.
Su sucesor es p₅: p₇p₅p₃ no converge.

Insertar vértice y arista-extremos para p₅p₃p₁:

D = p₁-p₂ p₂-p₃ p₂-p₄ p₃-p₁ p₃-p₅ p₁-p₄ p₄-p₃ p₄-p₆ p₄-p₇ p₁-p₆ p₆-p₇ p₇-p₃ p₇-p₅ p₅-p₁
p_c321 p_c124 p_c423 p_c146 p_c647 p_c743 p_c735 p_c531

Eliminar arco central p₃:

LP = p₁p₆p₇p₅p₁

Verificar (en la nueva línea de playa) tripletas involucradas con el sitio eliminado p₄:

Su predecesor es p₅: p₇p₅p₁ no converge.

Su sucesor es p₁: pspipnohay no procede.

Hemos finalizado. El diagrama de Voronoi para el ejemplo es este:

D = p₁-p₂ p₂-p₃ p₂-p₄ p₃-p₁ p₃-p₅ p₁-p₄ p₄-p₃ p₄-p₆ p₄-p₇ p₁-p₆ p₆-p₇ p₇-p₃ p₇-p₅ p₅-p₁
p_c321 p_c124 p_c423 p_c146 p_c647 p_c743 p_c735 p_c531

Podría verse así, algunas aristas y vértices presentes en D se señalan con flechas torpemente dibujadas: