Services on Demand
Article
Indicators
Related links
 Cited by SciELO
Cited by SciELO
 Similars in SciELO
Similars in SciELO
Bookmark
Revista Investigación y Tecnología
Print version ISSN 2306-0522
Rev Inv Tec vol.4 no.1 La Paz Oct. 2016
SIMPOSIO EDUCACIÓN Y TIC’S
Pensamiento Algorítmico en la Matemática de la Enseñanza Básica
Algorithmic Thinking Mathematics in Basic Education
*Ph.D. Javier Alanoca Gutierrez
Facultad de Ingeniería-UPSA
Ingeniería de Sistemas Universidad Privada de Santa Cruz de la Sierra-UPSA
Santa Cruz de la Sierra - Bolivia Autor de correspondencia: *javieralanoca@upsa.edu.bo , fai@upsa.edu.bo
Presentado: Santa Cruz de la Sierra, 19 de septiembre de 2106. Aceptado: La Paz, 10 de Octubre de 2016.
Resumen
La matemática siempre ha estado vinculado a los algoritmos desde los inicios de la aparición del algebra, con diferentes denominaciones: algoritmia, algorismo y finalmente algoritmo, muy bien adoptados por los informáticos y programadores, por la exigencia y rigor con la que expresa este cuando se vierte en un procedimiento preciso, ordenado y lógico como sería en un lenguaje C. La enseñanza de la matemática se ha centrado en soluciones y procedimientos operativos y algebraicos que no precisan las diferencias, condiciones, y la interpretación de soluciones variadas que puede haber en un modelo matemático o en un problema bajo ciertas características de los datos fuente. El tema de pensamiento algorítmico y pensamiento matemático se trata de forma separada, siendo que la matemática puede ayudar a un buen desarrollo de los algoritmos y por lo tanto a un aprendizaje profundo de la matemática. En este ensayo se trata de relacionar ambos conceptos, la matemática y algoritmo como un sistema de colaboración para el aprendizaje de la matemática y la programación. Los argumentos se los encuentra en los mejores referentes como Knuth, Turing, Von Neuman y Putman, de ahí la valides todavía de estos gurús clásicos de la matemática y computación, acompañado hoy para su práctica y enseñanza por lenguajes visuales y descriptivos como el PseInt, Scratch, lenguaje C entre otros. Este ensayo está dirigido a la reflexión de en la enseñanza básica, para fortalecer todas las iniciativas que se están dando para apoyar un mejor desarrollo de la matemática y de la programación.
Palabras clave: Pensamiento algorítmico; Pensamiento matemático; Algoritmo; Lógica de la programación.
Abstract
Mathematics has always been linked to the algorithms since the beginning ofthe emergence of algebra, with different denominations: algoritmia, algorism and finally algorithm, well adopted by computer scientists and programmers, by the demands and rigor with which he expresses this when poured into a precise, orderly and logical procedure would be in a language like C. the teaching of mathematics has focused on solutions and operational and algebraic procedures that do not require the differences, conditions, and interpretation of various solutions that may be in a mathematical model or a problem under certain characteristics of the source data. The theme of algorithmic thinking and mathematical thinking is separately being that mathematics can help a good development of algorithms and therefore a deep learning of mathematics. This essay tries to relate the two concepts,
mathematics and algorithm as a collaborative system for learning mathematics and programming. The arguments are found in the best refer ences as Knuth, Turing, Von Neuman and Putman, hence the validity yet these classic gurus of mathematics and computer science, joined today for practice and teaching visual and descriptive languages such as PseInt, Scratch, C language among others. This essay is aimed at reflection in basic education, to strengthen all the initiatives that are being taken to support better development of mathematics and programming.
Keywords: Algorithmic thinking; Mathematical thinking; Algorithm; Logic programming.
Introducción
La propuesta de la ponencia está en base a la investigación de la presentación de un modelo didáctico para el desarrollo de la lógica de la programación mediante objetos de aprendizaje (Alanoca J. 2007). En este ensayo haremos una revisión de la parte fundamental de la programación buscando un vínculo de la aplicación algorítmica a la enseñanza de la matemática, fundamentalmente reducir la brecha y las insuficiencias de la enseñanza de la matemática con el pensamiento algorítmico. Este abordaje no es nuevo, pero las propuestas no muestran los detalles algorítmicos y matemáticos vinculados, que ayuden a identificar no solo las operaciones principales de los modelos matemáticos, sino las excepciones, condiciones que definen la valides de una solución rigurosa y completa.
La estructura de la computadora permanece en el modelo de Von Neumann desde los años 1947, y la máquina abstracta de Alan Turing, los principios fundamentales de la lógica de la programación han permanecido inalterables en el tiempo de la era de la computación. Su origen principal fue facilitar la realización de cálculos complejos, para que los humanos puedan delegar esta tarea tediosa a la computadora. Mediante el método del análisis histórico-lógico, se revisó el ánimo de la filosofía actual, comenzado en los finales del siglo pasado, donde se inició una renovación epistemológica, motivado por el surgimiento y consolidación de nuevas ciencias como la informática y los progresos científicos modernos. Hoy hablamos de la epistemología de la informática o de la ingeniería, que aún están en sus inicios, pero con un avance vertiginoso, que conlleva a una redefinición de los límites de la epistemología incorporando necesidades de nuevas teorías. Es así que Putman (2000) en su libro "Cómo renovar la filosofía", inicia la propuesta del replanteamiento de la filosofía, en su primer capítulo "El proyecto de la inteligencia artificial", plantea el cuestionamiento de la teoría única que lo explica todo, ya iniciada este análisis por Jhon Dewey. El ser humano desea resolver una serie de problemas en todos los campos del saber, desde una reflexión filosófica hasta el desarrollo de tecnología para fines específicos de instrucción, producción e investigación. De esta forma, Putman (2002) en su llamado cambio de actitud, examina algunos argumentos utilizados por los filósofos para mostrar que la ciencia cognitiva moderna explica el vínculo entre el lenguaje y el mundo, que expone bases del crecimiento ontogénico de las personas.
El primero trata sobre la inteligencia artificial, el segundo analiza la teoría evolutiva, clave de los misterios de la intencionalidad, y el tercero examina la afirmación del filósofo Jerry Fodor, quien señala que se puede definir la teoría de la referencia en términos de nociones causales/contrafácticas. Textualmente Putman indica lo siguiente:
"En particular pretendemos demostrar que se puede y se debe aceptar la idea de que la psicología cognitiva no se reduce a, como tanta gente (incluidos la mayoría de los "científicos cognitivos") supone, una mera ciencia del cerebro inseparable de la informática" (Putnam, 2002).
Esto conduce a una propuesta del estudio de la mente, como comparándola con las computadoras desde un punto de vista físico, abriendo un vasto campo para la creación de una epistemología de la informática, considerando la mente como una especie de calculadora, cada una con limitaciones y ventajas. Una computadora puede retener y recuperar grandes cantidades de información, procesar operaciones matemáticas complejas, tareas difíciles para los seres humanos. Mientras que la mente de los seres humanos es capaz de inferir y crear respuestas ante situaciones completamente nuevas, con sentimientos, actitudes y valores, los cuales son difíciles de imitar por una computadora, esto por ahora, si lo tuviera estaríamos hablando de inteligencia artificial. Esto induce a una pregunta básica, ¿puede una computadora tener inteligencia, conciencia, y otras capacidades como los seres humanos?, es a partir de este tipo de preguntas, que el ser humano ha encontrado una forma de conocerse así mismo modelando la inteligencia de las computadoras a la imagen de él mismo, con lo cual ha podido lograr a su vez una mejor comprensión del proceso de aprendizaje de las personas. Por todo esto, recurrimos a los fundamentos de la lógica de la programación que deben ser impartidas desde los inicios de la enseñanza básica, y la matemática se presta idealmente para este objetivo.
Métodos
La Arquitectura de la Von Neumann
La meta de los científicos informáticos es que las computadoras puedan desarrollar sus capacidades de cálculo hasta llegar a equipararse con el cerebro humano. Sin embargo, esto será un largo proceso de desarrollo de algoritmos complejos, mezclados con la bioinformática y otras tecnologías, hasta lograr imitar la arquitectura y las funcionalidades del cerebro humano y tal vez superarlo en algunos aspectos y en otros no lograr nada. Sin embargo, hasta el momento, la arquitectura de la computadora diseñada por Von Neumann (Brassard, 1998; Riley, 1987) no ha sufrido cambios sustanciales, más que un progreso en cuanto a capacidades de reducción de la infraestructura de la parte electrónica, el aumento en velocidad de procesadores y crecimiento de memoria. De esta manera, se halló que hubo tres elementos de inspiración de la computadora. Primero, el cerebro humano sobre cuya base se modeló la arquitectura de la computadora. El segundo inspirador para esta investigación, es la Máquina de Turing, diseñado por el Británico Alan Turing, máquina abstracta que refleja una manera propia de ver el funcionamiento del cerebro humano. En su versión de máquina de Turing universal es capaz de imitar una amplitud de clases de máquina como: la computadora, las máquinas biológicas y químicas. El tercer elemento inspirador, fue expresado por el Húngaro John Von Neumann, quién formuló las bases del diseño de las computadoras contemporáneas del siglo XX mediante el diseño llamada la Arquitectura de Von Neumann, la misma que no ha sufrido mayores cambios conceptuales a la fecha, aunque existen propuestas como las máquinas cuánticas y las basadas en estructura neuronal.
Algoritmos y Programación
La sistematización realizada, permite identificar que el concepto de algoritmo representa básicamente la lógica de la ejecución de un programa, inmerso su desarrollo dentro la actividad de la programación. Los algoritmos tienen como característica importante la independencia de los lenguajes de computadoras, permitiendo enfocar la atención, en su fase creativa, en el diseño de la lógica de un algoritmo. No todos los algoritmos necesariamente se traducen a un lenguaje de programación, tal es el caso de las recetas de cocina, que también son clasificados como algoritmos. El diseño de los algoritmos incluye métodos muy importantes como la modelación y creatividad para la solución de un problema. Una vez construido el algoritmo, éste se traduce a un lenguaje específico de computadora, como el "lenguaje C", este a su vez, es traducido al lenguaje objeto que entiende la computadora. Es muy importante comprender el concepto de algoritmo y mediante un análisis histórico-lógico comprender lo que encierra este término, desde su origen histórico hasta su desarrollo y aplicaciones recientes.
Según Knuth (1980) y del diccionario Webster's New World Dictionary desde 1957 denominada en su forma antigua "algorismo" con su antiguo significado de "el proceso de hacer aritmética usando guarismos arábicos". Después de un largo tiempo los historiadores encontraron el origen auténtico de la palabra algorismo: viene del nombre del autor de un famoso libro de texto persa, Abu Ja'far Mohammed ibn Mûsâ Al-Khowârizmî (825), literalmente: "Padre de Ja'far, Mohammed, hijo de Moisés, natural de Khowârizm". Khowârizm es una ciudad Soviética de Khiva. Al-Khowârizmî escribió, el célebre libro de Kitab al jabr w'al-muqabala ("Reglas de restauración y reducción"); otra palabra, "álgebra", procede del título de su libro, aunque, el libro no fuese realmente muy algebraico. Paulatinamente la palabra algorismo fue corrompiéndose, hasta llamarse algoritmo, este cambio no se entiende, teniendo en cuenta que la gente se había olvidado su derivación original.
Otra versión corresponde a (Knuth, 1980) según el cual la palabra algoritmo procede del nombre del matemático árabe (uzbeko) al-Jwârizmi que en el siglo IX elaboró las reglas de las cuatro operaciones aritméticas sobre los números en el sistema decimal de numeración. El conjunto de estas reglas recibieron en Europa el nombre de "algoritmia". Posteriormente esta palabra se transformó en "algoritmo", convirtiéndose en la denominación colectiva de reglas aisladas de un tipo determinado (y no sólo de las reglas de operaciones aritméticas). Durante largo tiempo la palabra algoritmo la empleaban sólo los matemáticos, designando las reglas de solución de diversos problemas.
El estudio histórico-lógico permite descubrir que, en los años 30 del siglo XX, la palabra algoritmo se hizo popular con la aparición de las computadoras. El desarrollo de los medios electrónicos y los métodos de programación contribuyeron a la comprensión de que la elaboración de los algoritmos es una etapa indispensable de la automatización. En la actualidad, la palabra algoritmo rebasó los márgenes de las matemáticas.
Hasta hoy en día, no finalizó la formación del concepto científico de algoritmo, que se convirtió en un problema importante. A pesar de que la teoría de algoritmos es una disciplina matemática, ella todavía no se parece mucho a las ciencias bien conocidas, como la geometría o la teoría de los números.
Noción intuitiva de algoritmo.
Según Krinitski (1988) en las diversas reglas con las que nos enfrentamos cotidianamente, una función peculiar pertenece a las reglas que señalan una secuencia de operaciones que conducen al logro de cierto resultado indispensable. Con frecuencia hoy en día se las denomina algoritmo.
Llamaremos intuición al conocimiento adquirido debido a una gran experiencia, pero aún no sometido a un análisis científico, por lo que resulta insuficientemente impreciso y estricto. A medida que se va acumulando experiencia, este conocimiento se enriquece y por eso nuestras nociones intuitivas sobre algo pueden variar paulatinamente.
Los conocimientos expresados en forma científica, en forma matemática, no poseen tanta variedad, se caracterizan por una mayor precisión y sirven de base para las deducciones científicas.
Algunos ejemplos servirán para explicar en sentido intuitivo el concepto de algoritmo. Las reglas que prohíben algo: "La entrada a gente ajena está prohibida", "Prohibido fumar", "Entrada prohibida", "Permitida la parada", "Área de fumar", todos estos avisos, no pertenecen a la clasificación de algoritmos. Sin embargo, las reglas: "Al marchar, apáguese la luz", "subir al piso 4 por ascensor y seguir por la derecha hasta la habitación 415", se puede decir que ya son en sí algoritmos, aunque cotidianos Krinitski (1988). Es necesario, señalar una peculiaridad del algoritmo: el carácter discreto del proceso que se determina por el propio algoritmo. La regla "Al andar por la acera, manténgase a la derecha", a pesar de ser una prescripción, tiene un carácter continuo (no finito), por lo que no es un algoritmo.
Hay otro tipo de algoritmos, por ejemplo: "A cada cachorro se le debe de alimentar separado de los demás, de lo contrario los cachorros más fuertes y activos comerán la mayor porción. Se los sobrealimenta 3 a 4 veces al día, después de mamar en pequeñas porciones iguales, comenzando con medio vaso de leche". En esta regla la frase "...de lo contrario los cachorros más fuertes y activos comerán la mayor porción" no pertenece a la propia regla de los algoritmos. Semejantes frases se denominan comentarios. Si se prescinde de ellos, el sentido de la regla no cambia.
También las recetas de cocina suelen constituirse en una verdadera colección de algoritmos. Al igual que en la prescripción de las recetas médicas donde la vida de las personas depende de la exactitud con que se cumpla el procedimiento prescrito por el médico.
Las personas, independiente del sexo, edad, ocupación ejecutan cotidianamente algoritmos, aunque no lo expresen como tal. Dejándose guiar por la intuición base para desarrollar los algoritmos, basado en la razón o el sentido común. Hay una variedad de tipos de algoritmos, como los algoritmos relacionados a la vida cotidiana, a los procesos de cálculo y de gestión. Esto invita al estudio de la complejidad de los algoritmos desde la perspectiva matemática, recientemente se habla de algoritmos genéticos, algoritmos neurales, queriendo potenciar la ejecución de las computadoras imitando ciertas funciones del pensamiento humano.
Las definiciones más modernas de algoritmos según Brassard (1998) se encuentran en la última edición del DRAE (Diccionario de la Real Academia Española), donde se define siguiente: Algoritmia "Ciencia del cálculo del cálculo aritmético y algebraico; teoría de los números".
Algoritmo "1. Conjunto ordenado y finito de operaciones que permite hallar la solución de un problema; 2. Método y notación en las distintas formas del cálculo".
Según Brassard (1998) un algoritmo es un conjunto de reglas para efectuar algún cálculo, bien sea a mano o, más frecuentemente, en una máquina. Las máquinas pueden ser las computadoras existentes hoy como son la PC o también podrían ser máquinas abstractas como la de Turing o de Post.
Precisando la definición de algoritmo.
En términos que los algoritmos tienen que ser ejecutados por máquinas reales se requiere de definiciones más precisas y estructuradas. De éstas, hay muchas definiciones, al revisar los mismos vemos que tienen puntos coincidentes. Estas enfatizan o condicionan la esencia del trabajo que deben ejecutar los algoritmos. Estos requieren datos de entrada, producen un resultado a través de operaciones definidas en un cierto tiempo definido. Siguiendo se da una definición usual.
Según Knuth (1998) un algoritmo debe cumplir cinco condiciones importantes:
(i) Finitud. Un algoritmo tiene que finalizar la ejecución de las instrucciones tras un número finito de pasos.
(ii) Definibilidad. Cada paso de un algoritmo debe definirse de modo preciso; las acciones a realizar están especificadas rigurosamente y sin ninguna ambigüedad.
(iii) Entrada. Un algoritmo puede tener cero o más entradas, es decir, en algunos casos un algoritmo puede iniciar su ejecución con datos generados internamente, o de uno o más datos provistos externamente.
(iv) Salida. Un algoritmo tiene una o más salidas (resultados), es decir, que tienen una relación específica con los datos de entrada y el proceso algorítmico ejecutado.
(v) Efectividad. Por lo general, se pretende que un algoritmo sea efectivo. Esto significa que todas las operaciones a realizar en el algoritmo deben ser bastante básicas para ser efectuadas de modo exacto y en un lapso de tiempo finito por un hombre mediante papel y lápiz.
Otra definición de algoritmo, propuesta por Turing en base a su máquina de estados finitos, dice, algoritmo es todo aquello que puede ser ejecutado por la máquina de Turing.
Fundamentos de la Programación.
El análisis documental, sobre la programación y su enseñanza, posibilita averiguar que la ejecución de las instrucciones por la computadora es básicamente secuencial en diferentes niveles de lenguajes, desde el lenguaje de máquina que es la que ejecuta la computadora, pasando por el lenguaje ensamblador hasta los lenguajes de alto nivel, entendibles por el ser humano. Cualquiera sea la metodología de programación (secuencial, estructurada, modular, orientado a objetos) existen ciertas invariantes básicas, desde la perspectiva del nivel del lenguaje de máquina o lenguaje ensamblador, básicamente hay secuenciación de instrucciones, ejecución de condiciones y control de saltos o bifurcaciones. Con la ejecución de condiciones se puede ejecutar o no ciertas instrucciones dependiendo del estado de los datos, y de igual forma con esta función se puede realizar procesos repetitivos a través de los saltos hacia atrás. En otro nivel de programación, desde la perspectiva de lenguajes de alto nivel, es posible definir los programas desde un nivel llamado programación estructurada, modular, u orientado a objetos, donde las invariantes básicas son: la secuencia, la selección y la repetición, al margen de la metodología de programación que cada uno sigue. Pudiéndose evidenciar que existe una equivalencia entre las invariantes de un lenguaje de bajo nivel y un lenguaje de alto nivel, siendo este último cercano al lenguaje del ser humano.
La programación estructurada.
Este enfoque de la programación parte de que todo programa debe ser leíble y mantenible por terceras personas. El teorema de Dijkstra, demostrado por Edsger Dijkstra en los años sesenta, nos demuestra que todo programa se puede escribir utilizando únicamente tres instrucciones de control que son {Instrucción secuencial, Instrucción condicional if, Instrucción repetitiva while}. Las ventajas de la programación estructurada son:
1) Los programas son leíbles de forma secuencial, sin necesidad de hacer seguimiento a los saltos.
2) La estructura del programa es clara, debido a que las instrucciones están más cohesionadas.
3) Las pruebas son más fáciles de realizar, por lo tanto, los errores son fáciles de detectar debido a que la lógica del programa es más evidente.
4) Se reducen los costos de mantenimiento.
5) Los programas son más sencillos y rápidos.
6) Los bloques de código son autoexplicativos, debido a su cohesión.
Estructuras Básicas
Buscando en la psicología educativa el marco referencial de esta investigación, se halló que la estructura de la mente es muy compleja, principalmente si quisiéramos saber cómo actúa el cerebro frente a la lógica de la programación en la elaboración de programas (Woolfolk, 2006). Por el otro lado, ser un buen matemático, no necesariamente implica que pueda tener iguales capacidades para la programación, la programación sigue y construye su propia lógica siguiendo patrones sencillos y composiciones complejas. Esto significa que la programación sigue sus propios métodos y paradigmas, no obstante que cada persona aprovecha sus recursos de lógica y matemática de forma particular. Tener un buen dominio de las matemáticas ayudará a tener más herramientas y posibilidades de resolver problemas complejos de programación. Sin embargo, independiente de lo anterior, el cerebro actúa en la programación y su aprendizaje en pasos pequeños usando pequeños objetos de su dominio o conocimiento. Por lo mismo, busca patrones o modelos que permitan avanzar a la búsqueda del conocimiento y solución de problemas. Los modelos o patrones son estructuras básicas como son la realización de un cálculo de una fórmula, como sería calcular el área de un rectángulo. Primero se busca tener claro el objetivo (área), segundo se busca los insumos con las que se realizará el cálculo (base y altura), seguidamente se busca la fórmula que permita alcanza el objetivo. En el nivel del lenguaje de las computadoras, se requiere ejecutar ciertos pasos previos antes de obtener el programa. Estos pasos, exigen el conocimiento de un lenguaje de elaboración del algoritmo (procedimiento) en términos que sean lo más cercano al lenguaje de las computadoras.
Discusión
El aprendizaje de la matemática en la enseñanza básica, enfatiza los aspectos operativos que resuelven el problema principal, como hallar el valor de una variable x, o y en un sistemas de ecuaciones, olvida o no enfatiza las excepciones, cuando se presenta una indeterminación o sale del campo de los números reales al campo de los complejos, su interpretación será diferentes en uno u otro dominio de solución esperada. Si enfocamos la resolución de un problema desde la perspectiva algorítmica, es posible caracterizar la solución y los pasos que lo llevan a esta, permitiendo el aprendizaje en los puntos de indeterminación, u otro espacio de solución diferente. Por el otro lado, está el problema de identificar los diferentes tipos de solución viables, o las factibles, la identificación de las excepciones que se dan en los datos, o en cierta conformación de los datos.
Este enfoque algorítmico lo veremos con los modelos matemáticos conocidos de fácil comprensión y análisis. Primero, estableceremos el análisis de la solución planteada en el modelo, luego ordenaros algorítmicamente la solución en un esquema llamado Diagrama de Flujo, luego se hace la verificación de que este funciona lógicamente en todos los casos de datos posibles (en el ámbito informático este se llama testing), a todo este proceso de desarrollo o análisis llamaremos pensamiento algorítmico en la matemática. De forma directa, está claro que esto nos lleva al aprendizaje de la programación en algún lenguaje gráfico, simbólico, como serían los conocidos lenguajes: PseInt, Lenguaje C, Java, etc.
El aprendizaje de la programación pone muchos retos a los estudiantes que están iniciándose en la programación, y en nuestro caso a los que están aprendiendo matemáticas de forma más precisa. Estos retos tienen que ver con la comprensión de problemas que puedan ser resueltos por computadoras, desde aquellas que tienen que realizar un simple cálculo como hallar el volumen de un cuerpo, es decir, una primera fase de entendimiento es la correcta formulación de problemas programables y que puedan ser escritos en términos del lenguaje que entiendan las computadoras. Luego comprender el accionar repetitivo que debe ejecutar una computadora para determinados tipos de problema, como son los cálculos de algunas series, sumatorias y acumulaciones de datos. Otro tipo de problemas fundamentales de programación al igual que en la matemática, es la identificación de restricciones, como sucede en la evaluación de una ecuación de segundo grado de una incógnita, es decir, que las raíces negativas producen soluciones complejas, de igual forma identifican las excepciones de indeterminación como es la división entre cero o condiciones que los problemas por sí solo no lo expresan, por lo mismo, muchas veces se omiten su programación o interpretación matemática, hasta que se produce la situación inexplicada, por haber obviado el análisis de ciertas condiciones, del modelo, siendo que en la realidad si tienen una interpretación, esto puede ser catastrófico en los sistemas donde la vida de las personas depende de las máquinas o modelos matemáticos, como ha sucedo con muchas fallas de programas o modelación matemática.
Analicemos el problema de la ecuación cuadrática:
ax2 + bx + c = 0
Esto se puede resolver por alguno de los métodos conocidos:
1. Factorización Simple
2. Completando el Cuadrado
3. Fórmula Cuadrática
Si resolvemos la ecuación de forma analítica o genérica, después de un proceso deductivo para obtener la solución a la ecuación, se debe llegar a expresar la siguiente fórmula:
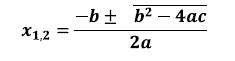
Los valores que se conocen son a, b, c R. Como se ve en la fórmula hay dos soluciones básicas x1 y x2, que no indican si los resultados pueden reales o complejos. Sin embargo, hay indeterminaciones, en el campo de los números reales, cuando el discriminante b2 - 4.a.c < 0 es negativo, no hay raíces cuadradas de números negativos, el cálculo es llevado al campo de los números complejos. La otra pregunta inmediata es, qué pasa si la constante a es cero, obviamente, la matemática reduce la ecuación, a una de primer grado: bx + c = 0; sin embargo, la computación genérica que pueda hacer una máquina debe poder prever esta situación, como dándole cierta inteligencia al programa para poder caracterizar ecuaciones, esta misma situación lo debe hacer un estudiante de un curso de matemáticas, evaluar las excepciones y los diferentes tipos de resultados.
Con estas consideraciones escribimos el algoritmo con PSeInt (Fig. 1) y en seudo-código (Fig. 2).
El programa de la Figura 2 responde a las necesidades planteadas, es decir, obtiene el resultado cuando la ecuación se hace simple y obtienes las soluciones reales y complejas. Queda un pequeño detalle por manejar, ¿qué pasa si a y b son igual a cero?, obviamente no existe la ecuación. En este caso, el programa de la Figura 2, no sabe manejar esta situación, por lo tanto, se producirá la falla cuando alguien introduzca estos datos (a y b con valor cero).
La siguiente ecuación de la figura 3 tiene soluciones reales, la gráfica es una parábola que cruza el eje x en los puntos -5 y 3
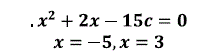
La siguiente ecuación de la figura 4 tiene solución compleja, observamos que la parábola no cruza el eje x, pero existe!.
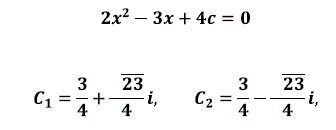
Finalmente, haremos un breve resumen de algunas herramientas, como sugerencia, para promover el pensamiento algorítmico aplicado a las matemáticas (Ríos, 2014).
Herramientas para promover el pensamiento algorítmico
1. Diagramas de flujo con PseInt. Visualizan las operaciones, condiciones y repeticiones de forma clara. Es muy útil para la comprensión lógica y codificación en un lenguaje como C. Su uso ha transcendido a otros ámbitos profesionales donde se requiere que las personas pueden comprender los flujos de datos e información de forma clara siguiendo los flujos.
2. Scratch. Es ideal para fomentar el desarrollo de animaciones de forma gráfica con objetos lúdicos, lo cual lo hace atractivo a los niños y a los jóvenes planteándoles objetivos atractivos. Se lo encuentra en: http://scratch.mit.edu/
3.- Blockly. Es una herramienta visual de programación básica como una alternativa a scratch, se programa en la web por google: https://developers. google. com/blockly/
4.- El lenguaje C. Una opción ideal para implementar programas desde los más simples hasta los más complejos. Existe una variedad de compiladores para el lenguaje C.
Conclusiones
Las iniciativas son varias, en el sentido de promover el pensamiento algorítmico aplicado a las matemáticas, siendo un recurso importante en diferentes niveles de enseñanza de las matemáticas.
Mediante el análisis documental se definen que hay tres estructuras fundamentales para el desarrollo de la lógica de programación, que están en conformidad a los modelos de la máquina de Von Neuman y la máquina de Turing. Estas tres estructuras son: el control de la secuencia, el control de la selección, y el control de repetición. A lo largo del proceso de aprendizaje estas tres estructuras mentales deben ser internalizados por los estudiantes como parte de los procesos psicológicos superiores colaborados por los objetos de aprendizaje y el profesor. En forma paralela al proceso de aprendizaje de las estructuras lógicas de programación, el estudiante debe ir apropiándose de tres lenguajes: el lenguaje seudocódigo, el lenguaje de los diagramas de flujo y el lenguaje de programación C, de acuerdo al modelo didáctico conceptual basado en el paradigma del constructivismo social.
Referencias
Alanoca, J. (2007). Modelo Didáctico para el Desarrollo de la Lógica de la Programación Mediante Objetos De Aprendizaje. Bolivia: UMRPSFXCH. [ Links ]
Brassard, G. y Bratley P. (1998). Fundamentos de Algoritmia. España: Prentice Hall. [ Links ]
Knuth, Donald E. (1980). Algoritmos fundamentales (Volumen I). España: Editorial reverte, s.a. [ Links ]
Krinitski, N. (1988). Algoritmos a nuestro alrededor. URSS: Editorial Mir Moscú. [ Links ]
Putnam, H. (2002) Cómo renovar la filosofía. Madrid: Ediciones Cátedra (Grupo Anaya, S. A. ). [ Links ]
Woolfolk, A. (2006). Psicología Educativa. México: Editorial Pearson. [ Links ]
Ministerio de Educación Colombia. (2010). La ciencia de la computación no es solo para universitarios. Recuperado el 10-09-2016, de http://www.mineducacion.gov.co/cvn/1665/w3-article-241894. html [ Links ]
Rios, J. (2014). Herramientas para desarrollar el pensamiento algorítmico. Recuperado 04-09-2016, dehttp://www.gestiopolis.com/herramientas-para-desarrollar-el-pensamiento-algoritmico/ [ Links ]