Servicios Personalizados
Articulo
Indicadores
Links relacionados
 Citado por SciELO
Citado por SciELO
 Similares en SciELO
Similares en SciELO
Bookmark
Revista Institucional de Ciencias, Tecnología e Innovación Investig@ UMSA
versión impresa ISSN 2220-7139
Investig@ UMSA v.2 n.2 La Paz 2011
ARTÍCULOS
MODELADO DE UN GRUPO GENERADOR SÍNCRONO - TURBINA HIDRAÚLICA PARA SU ESTUDIO Y OPERACIÓN EN PEQUEÑOS SISTEMAS AISLADOS
Ing. Montaño Gonzales Emiliano
Instituto de Hidráulica e Hidrología, UMSA
Universidad Mayor de San Andrés - Bolivia Ciudad Universitaria, Calle 30 Cota Cota, La Paz
Msc. Ing. Montaño Saavedra Álvaro christian
Laboratorio de Control Inteligente, Departamento de Ingenieria Eléctrica,
UFES Universidade Federal do Espírito Santo. Becario CAPES/CNPq - IEL Nacional - Brasil Av.
Fernando Ferrari, 514, CEP 29075 - 910, Vitória - ES
E-mails: maqhidraulicas@hotmail.com, ecotecelm@yahoo.com
Artículo recibido en: julio del 2011
Artículo aceptado en: diciembre de 2011
RESUMEN
El presente trabajo muestra el montado y modelado de una planta formada por una turbina hidráulica y un generador síncrono para su funcionamiento como parte de una Micro Central Hidroeléctrica (MCH) para su operación en pequeños sistemas aislados. Una vez realizado el montado de la planta en laboratorio, se comienza con el desarrollo de un modelo empírico del proceso, en forma de curvas de reacción obtenidas utilizándose la técnica de respuesta al escalón; y que posibilitó la aproximación de las variables principales del proceso para un modelo de primera orden con tiempo muerto. Después de obtenidas las funciones de transferencia de la planta, se proyectó un controlador PID con la finalidad de mantener la tensión de salida del generador en un valor de referencia adecuado para su distribución en la red eléctrica del sistema aislado. Con el fin de validar los resultados obtenidos en las simulaciones, se obtuvieron curvas de respuesta del sistema real en laboratorio e se compararon ambas, dando un resultado parecido y satisfactorio. Estos resultados servirán como base para futuros estudios en las áreas de control de velocidad (o gobernador de carga) y estabilidad del sistema, entre otros, en el campo de las MCHs en pequeños sistemas aislados.
Palabras clave: Modelado; generador síncrono; turbina hidráulica; microcentral hidroeléctrica.
ABSTRACT
This work presents the assembly and modeling of a plant constituted by one turbine and one synchronous generator to function as a part of a Micro Hydroelectric Plant (MHP) for small isolated systems. Once the assembly of the plant at the laboratory was cons-tructed, has started the developing of an empirical model of the process in the form of reaction curves, obtained by the use of the step response technique that allowed the approximation ofthe main variables involved in a first order with dead time model. After obtaining the transfer functions of the plant, a PID controller was designed in order to maintain the output voltage ofthe generator on an appropriate reference value forelectri-cal distribution in the network ofthe isolated electric system. With the purpose of validate the simulation results, curves of response were obtained from the real system in the laboratory and were compared to both responses, giving a satisfactory and very similar result. These results will functionate as a basis for further studies in the areas of speed control (orcharge controller) and system stability, among others, in the field ofMHPs for small isolated systems.
Keywords: Design; synchronous generator; hydraulic turbine; hydroelectric microcentral.
INTRODUCCIÓN
En un sistema aislado, el grupo turbina hidráulica - generador necesita para su correcto funcionamiento de gobernadores o controles que lo mantengan funcionando a valores nominales de operación. Las variaciones en la potencia real (o activa) afectan principalmente a la frecuencia de la tensión generada, mientras que la potencia reactiva es menos sensible a estas variaciones y depende principalmente de las variaciones en la magnitud de la tensión. Por tanto, es posible controlar la potencia activa y la potencia reactiva de forma independiente. El lazo de control de de la potencia real - frecuencia LFC (load frequency control), controla la potencia real y la frecuencia (velocidad de rotación del generador); mientras que el lazo de control del regulador automático de tensión AVR (automatic voltage regulator) o de potencia activa - tensión regula la potencia reactiva y la magnitud de la tensión (Vanfretti, 2005).
La función básica de un sistema de excitación es de proveer corriente continua al bobinado de campo de una máquina síncrona. Además, el sistema de excitación desempeña funciones de control y protección esenciales para el funcionamiento satisfactorio del sistema de potencia a través del control de tensión de campo, y por consiguiente, de la corriente de campo. Las funciones de control incluyen el control de la tensión y de la potencia reactiva, como también el mejoramiento de la estabilidad del sistema (Vanfretti, 2007).
Los controles electrónicos de velocidad (o gobernadores de carga) se utilizan en pequeñas centrales que operan en sistemas aislados; estos mantienen la velocidad del conjunto turbina - generador constante desviando hacia un disipador (calentador de agua o aire) toda la energía eléctrica que no esté siendo consumida, para que esté disponible cuando sea requerida. Sumando las turbinas hidráulicas, los generadores, los controles de tensión y de frecuencia y los paneles de control, es posible montar grupos completos de generación hidroeléctrica.
En el presente trabajo es mostrado el proceso de identificación de los parámetros y la obtención del modelo dinámico de la planta, definida como el conjunto turbina hidráulica - generador eléctrico, a partir de pruebas experimentales en laboratorio en una planta montada para tal fin; para después realizar la sintonía del contro-lador de tensión de salida de la energía eléctrica generada, con el objetivo de obtener un modelo que sirva como base para futuras investigaciones sobre desarrollo y proyección de los controladores electrónicos de frecuencia, estabilidad del sistema entre otras, en pequeños sistemas aislados.
Elementos de la planta montada
Generador
El generador utilizado es síncrono tipo "BRUSHLESS", de tres fases con conexión en estrella con punto neutro; una
tensión de línea de 380 V y tensión de fase de 220 V, frecuencia de 50 Hz y factor de potencia de 0.8.
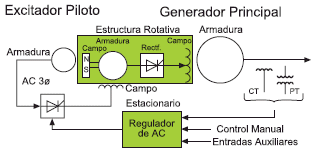
Figura 1. Sistema de excitación del generador sin escobillas
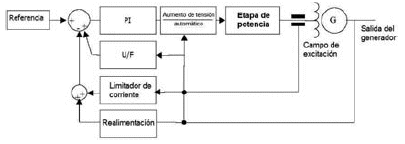
En la figura 2 se muestra la estructura del regulador de tensión.
Figura 2. Diagrama de bloques del AVR.
El funcionamiento del AVR está basado en la comparación del valor eficaz de la tensión de realimentación con la referencia de tensión, ajustada por la suma del trimpot de ajuste de tensión con el trimpot externo. El error es procesado por el lazo de realimentación cuyo valor determina el ángulo de disparo del tiristor que puede variar de 0 a 180°, controlando de esta forma la tensión de salida del generador. Con cero grados de disparo se tiene cero voltios en la salida del rectificador, y con disparo de 180 grados, se tiene la salida máxima dada por el rectificador de media onda.
Turbina hidráulica
En las pruebas en laboratorio fue usada una turbina tipo Banki, que admite un caudal máximo de 30 [l/s], diseñada para una altura de 40 [m] y con una potencia en el eje de 8 [kW].

Figura 3. Turbina hidráulica tipo Banki, fabricación IHH-UMSA
Planta montada
En la figu encionar notar que todas las pruebas fueron realizadas a velocidad constante, con ayuda de un gobernador electrónico de carga (f = cte.); esto fue hecho debido a que el sistema es básicamente un sistema linealmente independiente, o sea, que el control de tensión y de velocidad puede ser efectuado de forma independiente. Si no se hubiera utilizado el gobernador de velocidad hubiéramos obtenido datos que no reflejen el comportamiento real del generador, debido a que la respuesta también estaría influenciada por la inercia de los demás componentes de la planta (p.e. la turbina hidráulica).
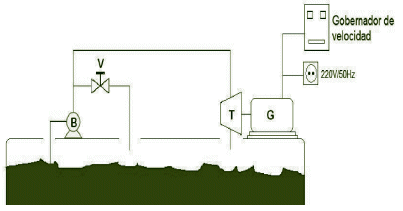
Figura 4. Sistema montado en laboratorio delIHH-UMSA
Obtención del modelo dinámico
Método de identificación dinámica a través del test escalón
Para la identificación de las características esenciales de un proceso bajo evaluación, es posible utilizar una entrada escalón. Así, el cambio abrupto a través de un incremento o decremento en la magnitud del escalón puede ser establecido en nuestro caso por la variación de la tensión de excitación.
En Coelho & Coelho (2004) se define un sistema lineal por medio de su respuesta al escalón para diferentes amplitudes en la señal de entrada (teorema de la superposición): "un sistema es lineal si la forma (curva) de la respuesta al escalón no depende de la amplitud de la señal de entrada", lo que es cumplido por las pruebas realizadas.
Los parámetros a ser estimados de los resultados obtenidos de un test escalón son: la ganancia del proceso, la constante de tiempo y el tiempo muerto.
3.2 Obtención del modelo de primera orden con tiempo muerto
Un modelo es una representación matemática de un sistema. Por ser un análogo matemático del sistema, se espera que el modelo sea representativo de las principales características del sistema real (Aguirre, 2007). Dado que el sistema puede sufrir perturbaciones tanto positivas como negativas (conexión o desconexión de la carga eléctrica a la salida del generador), en este estudio se utilizaron escalones positivos y negativos con la finalidad de observar el comportamiento de la planta en frente a estas perturbaciones. Por tanto, se obtuvieron dos funciones de transferencia que describen la dinámica del proceso.
Existen varios métodos para estimarla constante de tiempo de un proceso y el tiempo muerto a partir de la respuesta al escalón. El primero de estos métodos fue propuesto originalmente por Ziegler y Nichols (1942). Podemos llamar este método de "método de la tangente". Otros dos métodos, el "método del punto y de la tangente" y el "método de los dos puntos", dan resultados más próximos. En Corripio (2001) se encuentra que el "método de los dos puntos" resulta en una estimación más alta del tiempo muerto y una estimación más baja de la constante de tiempo del proceso en comparación con los otros dos métodos; por otro lado, el "método de la tangente" es el otro extremo. Por tanto, se decidió por utilizar el "método del punto y de la tangente".
Respuestas de la planta al test escalón sin AVR y obtención de las funciones de transferencia
Se obtuvieron las funciones de transferencia mediante el registro de las curvas de reacción de la tensión de salida del generador frente a escalones aplicados en la tensión de excitación de campo.
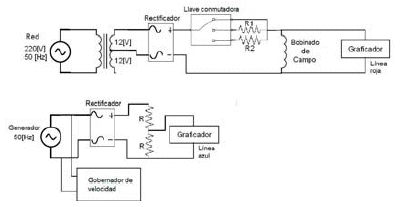
En la figura 5 el circuito utilizado para realizar las pruebas es mostrado.
Se realizaron varias pruebas, tanto para escalones negativos como para positivos; en la figura 6 se puede ver la respuesta del sistema al escalón positivo.
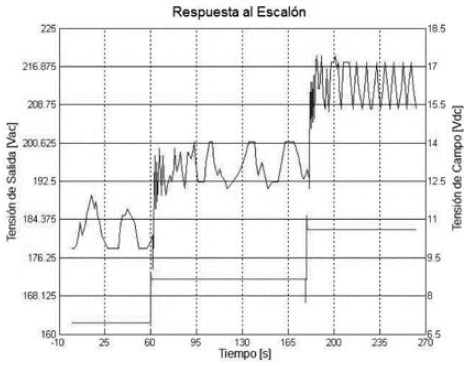
Figura 6. Escalones positivos en la tensión de excitación y respuesta del sistema
Se toman solo los datos del segundo escalón, debido a que se supone que la planta trabajará en un rango entre 190 - 240 [Vac] que son los valores recomendados por el fabricante del AVR para que este trabaje correctamente, se puede realizar una aproximación de la curva con ruido por una curva sigmoidal (Ferreira, 2000) como mostrado en la figura7.
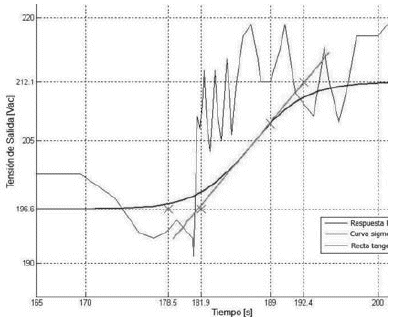
Figura 7. Curva de reacción del sistema y obtención de los parámetros para el modelado del proceso
Seguidamente, podemos ver un cuadro resumen de todas las funciones de transferencia encontradas en los distintos tests.

Cuadro 1. Resultados de las respuestas del proceso al test escalón
Modelo propuesto para el controlador de tensión
Sistema de control en lazo cerrado Una descripción detallada del diagrama funcional del sistema de control en lazo cerrado (SCLZ) es dada en la figura 8. Este diagrama muestra los principales componentes del sistema de control, siendo:
Referencia (SP): Valor deseado de la variable a ser controlada.
Comparador: Dispositivo que genera la señal de error entre el valor deseado y el obtenido.
Controlador: Dispositivo que manipula la señal de error, generando una señal de control que será aplicado en el sistema, a fin de corregir la variable a ser controlada.
Actuador: Dispositivo que recibe la señal de control y genera una señal con potencia suficiente para actuar sobre el sistema.
Sistema: Dispositivo o fenómeno que se desea operar con alguna finalidad (objetivo de control).
Medidor (transductor): Dispositivos responsables por la medición y conversión de la variable a ser controlada para fines de comparación y obtención del error de salida.
Output to Process (OP): Es la acción o señal de salida del controlador, en el presente caso, la tensión de excitación del generador (Edc).
Process Variable (PV): Es la variable del proceso o variable controlada, que en este caso es la tensión generada (Vac).
Manipulate Variable (MV): Es la variable manipulada a través del actuador, para este trabajo, es la intensidad de campo magnético para poder generar la FEM inducida.
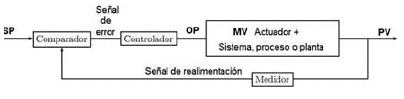
Figura 8. Diagrama del sistema de control en lazo cerrado
Estrategia de control utilizada
La controlabilidad del lazo decrece cuando la relación entre el tiempo muerto del proceso y su constante de tiempo se incrementan. Ahora podemos definir el parámetro de incontrolabilidad (Pu) del lazo como:

En Corripio (2001) un proceso con un tiempo muerto largo será incontrolable si su constante de tiempo es mucho mayor que el tiempo muerto. Para valores del parámetro de incontrolabilidad mayores que 1, el sistema será incontrolable. El cuadro 2 muestra el Pu para las funciones de transferencia obtenidas en el cuadro 1.
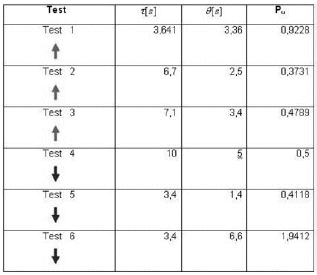
Cuadro 2. Controlabilidad de los tests realizados
Los parámetros estimados del test 6 dan como resultado un Pu>1, esto puede ser debido a muchas razones, como por ejemplo a la mala adquisición de los datos cuando fue realizado el test, uso incorrecto del registrador, error de los instrumentos de medición, etc. Por tanto, excluimos los datos del test 6 para los futuros cálculos.
Sintonía del controlador Según Aström & Hägglund (1995) el controlador PID es de lejos el algoritmo más común de control. Como fue mostrado en la figura 2, el AVR tiene incorporado un controlador PI, sin embargo, debido al tiempo rápido de respuesta del sistema con AVR, se decidió usar un controlador PID paralelo para poder representar de una manera más próxima el comportamiento real del AVR operando juntamente con la planta (generador-turbina hidráulica).
Como la finalidad es obtener una sintonía rápida y simple del sistema de control, utilizamos uno de los métodos más simples y efectivos propuesto para realizar la sintonía de controladores con realimentación (Corripio, 2001). Este método es conocido como reglas de sintonía IMC (Internal Model Control) y fue originalmente introducido con el nombre de "controller synthesis" en Martin (1976).
Para el modelo del proceso de primera orden con atraso, las reglas IMC de sintonía consisten en hacer el tiempo integral (Ti) igual a la constante de tempo (![]() ) del proceso y el tiempo derivativo (TD) igual a la mitad del tiempo muerto (
) del proceso y el tiempo derivativo (TD) igual a la mitad del tiempo muerto (![]() ) del proceso. La ganancia del proceso (KP) es después ajustado para obtener la respuesta deseada.
) del proceso. La ganancia del proceso (KP) es después ajustado para obtener la respuesta deseada.
Para una buena respuesta a disturbios, cuando Pu está entre 0.1 e 0.5, se usa la fórmula:

Cuando Pu es menor que 0.1 o mayor que 0.5 se debe usar solo la mitad de La ganancia como el valor inicial. Para una respuesta óptima a variaciones en el Set Point, cuando Pu está entre 0.1 a 0.5 y para un controlador PID usamos esta fórmula:
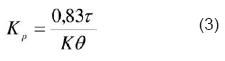
Las fórmulas anteriores confirman la idea de que la ganancia del controlador puede ser ajustado para obtener varios tipos de respuesta.
Estructuras del modelo del proceso Antes de definir las estructuras del modelo y efectuar la sintonía del controlador, debemos adaptar las unidades de las funciones de transferencia encontradas, esto es, la ganancia adimensional (% / %)![]() y
y![]() en minutos.
en minutos.
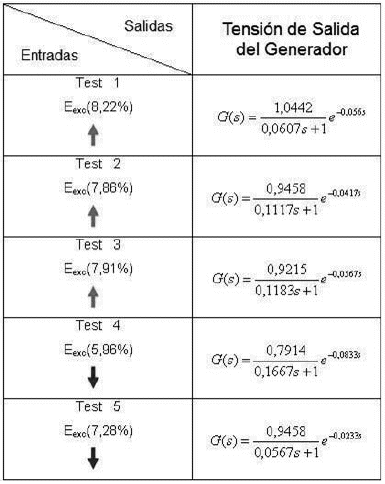
Cuadro 3. Funciones de transferencia con las unidades adaptadas
Después, se optó por tener una única función de transferencia, tanto para el test con escalón positivo como para el test con escalón negativo; para esto se obtuvieron los valores medios de cada uno de los parámetros de las funciones de transferencia.
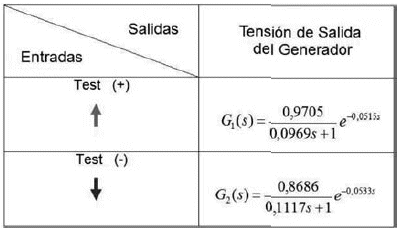
Cuadro 4. Media de las funciones de transferencia con las unidades adaptadas
La primera estructura propone la utilización de dos funciones de transferencia, y a partir de ellas, realizar la sintonía de los controladores PID para cada una de ellas.
Mientras que la segunda estructura de control propone que, en la identificación experimental del proceso, al repetirse un test escalón positivo y otro negativo, una media de los parámetros puede ser obtenida. En el cuadro 5 se puede ver un resumen de las funciones utilizadas en las dos estructuras.

Cuadro 5. Funciones obtenidas para las diferentes estructuras de control
5 Resultados en la planta real
La figura 9 muestra el diagrama de bloques de la planta utilizada para realizar los testes; en la figura 10 se muestran las conexiones del AVR para dar el escalón en la tensión de excitación.
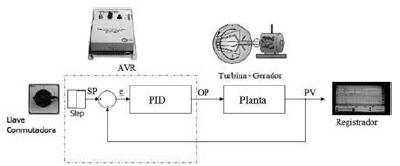
Figura 9. Lazo cerrado sometido a variación en el SP
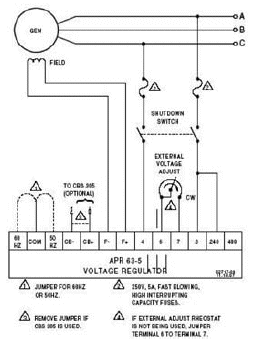
Figura 10. Diagrama de conexión del AVR
Como puede ser visto en la figura anterior, los pines 6 e 7 del AVR son utilizados para realizar un ajuste externo de la tensión de referencia (SP); en ellos fue instalado un conmutador con dos posiciones, una para colocarlos pinos en corto-circuito y el otro para conectar una resistencia de 1 [k![]() ]. Se debe mencionar que
]. Se debe mencionar que
inicialmente al generador se tienen conectados cargas eléctricas externas (resistencias de aire y focos), esto para permitir un correcto funcionamiento del AVR y poder alcanzar los valores nominales sin problemas.
En las figuras 11 y 12 se muestran las respuestas obtenidas a una entrada escalón positivo y otro negativo, empleando las simulaciones y en los testes en la planta real para la primera estructura de control.
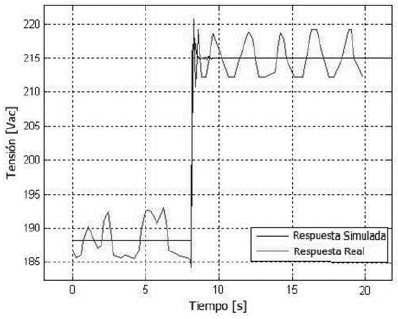
Figura 11. Respuesta del sistema al escalón positivo en el SP
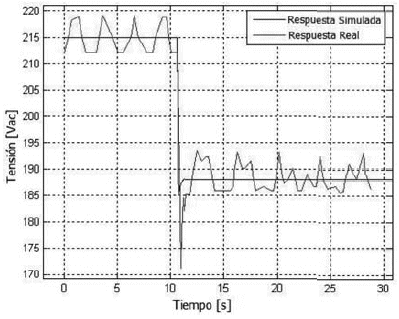
Figura 12. Respuesta del sistema al escalón negativo en el SP
En las figuras 13 y 14 se muestran las respuestas obtenidas para la segunda estructura de control.
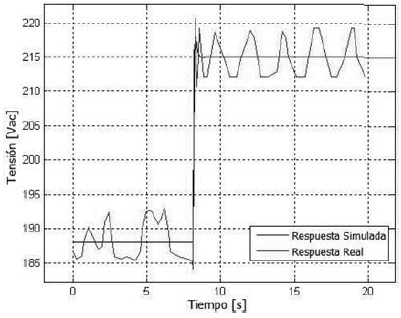
Figura 13. Respuesta del sistema al escalón positivo en el SP obtenida con la segunda estructura de control
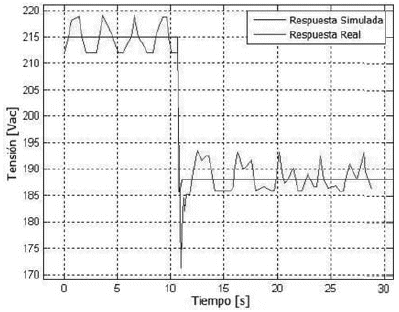
Figura 14. Respuesta del sistema al escalón negativo en el SP obtenida con la segunda estructura de control
Como se puede ver en las figuras 13 y 14, la utilización de una única función de transferencia y de un único controlador sintonizado vía IM da una respuesta bastante parecida con las obtenidas en el primer ensayo (estructura con dos funciones de transferencia), obteniéndose un error en régimen permanente nulo y un overshoot menor a 2% en ambas respuestas.
En la figura 15 es mostrada la planta real montada en laboratorio.

Figura 15. Planta para experimentación en laboratorio IHH-UMSA
6 Conclusión
En el presente artículo es presentado el modelo obtenido experimentalmente de la planta (generador-turbina hidráulica) y el controlador PID proyectado usado para controlar la tensión de salida de la energía eléctrica generada, que demostraron un comportamiento dinámico muy próximo con la de la planta real. Entonces es mostrado que una función de transferencia de primera orden con tiempo muerto puede representar el comportamiento del proceso de forma satisfactoria. El trabajo realizado podrá ser la base para futuros trabajos en lo que se refiere a investigaciones en las áreas de control de velocidad, estabilidad del sistema, entre otros, en el campo de las Micro Centrales Hidroeléctricas.
AGRADECIMIENTO
Los autores agradecen al IHH - UMSA, al Programa de Pôs-Graduação em Engenharia Eléctrica de la UFES y al Conselho Nacional de Desenvolvimento de Pessoal CNPq por todo el apoyo prestado durante la investigación.
BIBLIOGRAFÍA
Aguirre, L. (2007). Introdução à Identificagao de Sistemas. UFSC. SC. 580 p. Aström, K & Hägglund, T. (1995). PID Controllers: Theory, Design and Tuning. ISA, USA. 230 p. Coelho, A & Coelho, L.(2004). Identificagao de Sistemas Dinâmicos Lineares. UFSC. SC. 190 p. Corripio, A. (2001). Tuning of Industrial Control Systems. ISA, USA. 258 p. [ Links ]
Ferreira, E. (2000). Controle em Sistemas com Tempo Morto. Pp 63 - 95. Em: Proposta de Controle para uma Coluna de Destilação Didática. UFES. ES. 156 p. [ Links ]
Martin, J Jr. (1976). Howto Select Controller Modes and Tuning Parameters from Simple Process Models. ISA Transactions, Vol. 15, pp. 314-19. [ Links ]
Vanfretti, L. (2005). Modelación y Simulación de la Máquina Síncrona y su Operación en Sistemas de Potencia. 620 p. [ Links ]
Vanfretti, L. (2007). Sistemas de Control de Excitación y Estabilizadores de Sistemas de Potencia. 50 p. [ Links ]
Ziegler, J. G. & Nichols N. B. (1942). Optimum Settings for Automatic Controllers. Trans. ASME, 64, pp. 759 - 768. [ Links ]