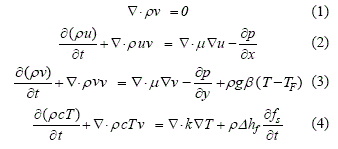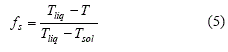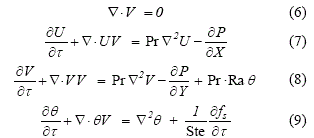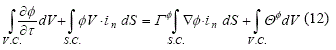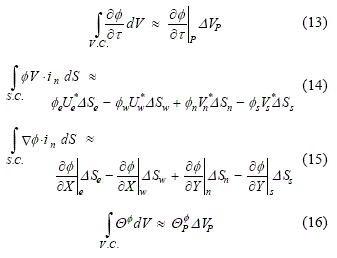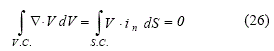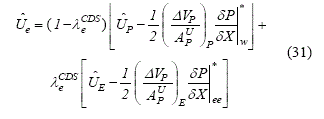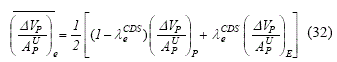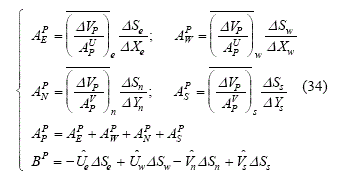ARTÍCULOS ORIGINALES

 

Simulación numérica de procesos de solidificación de aleaciones

 

 

Ing. Fernando S. Velasco Hurtado

 

 

---

Resumen

Una formulación numérica basada en el método de los volúmenes finitos y en el algoritmo de solución secuencial PRIME, destinada a la simulación detallada de procesos de solidificación de aleaciones metálicas en dominios bidimensionales, es desarrollada en el presente artículo. La formulación incluye los efectos del movimiento promovido por convección natural en la fase líquida, así como la liberación de calor latente en la región pastosa. El potencial de aplicación de la formulación presentada es evaluado mediante un ejemplo de simulación.

---

 

 

1.    INTRODUCCIÓN

La predicción detallada de la transferencia de calor en procesos de solidificación es fundamental para muchas operaciones metalúrgicas. Sin embargo, sólo en años recientes ha sido posible enfrentar las múltiples dificultades inherentes al tratamiento matemático de este tipo de problemas, gracias al desarrollo de equipos computacionales de gran capacidad. La presencia de movimiento promovido por convección natural en la fase líquida y la existencia de una interfase sólido-líquido que evoluciona con el tiempo son dos fenómenos que tornan complicada en exceso la descripción matemática de procesos de solidificación y hacen virtualmente imposible la obtención de soluciones analíticas.

El objetivo fundamental del presente artículo es el de mostrar los pasos principales en la construcción de una formulación numérica destinada a la obtención de simulaciones de la dinámica de procesos de solidificación de aleaciones metálicas. Para mayor simplicidad en la presentación, la formulación se ha restringido a problemas bidimensionales en geometrías rectangulares.

 

2.    MODELO MATEMÁTICO

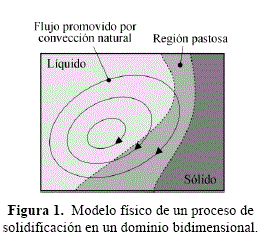
Según se muestra esquemáticamente en la figura 1, cuando una aleación sufre un proceso de solidificación, las fases sólida y líquida se hallan separadas por una región de mezcla bifásica denominada como región pastosa [3], que está delimitada por la temperaturas de sólido T_sol y de líquido T_liq y la cual calor latente es liberado. En la fase líquida y en la región pastosa, las fuerzas de flotación producidas por la leve variación de densidad debida a la distribución no uniforme de temperatura inducen el movimiento de fluido, fenómeno que es conocido como convección natural.

El modelo matemático de un proceso de solidificación, por tanto, debe comprender todas las ecuaciones que gobiernan el fenómeno de convección natural y debe incluir además la liberación de calor latente en la región pastosa. Para un caso bidimensional, este conjunto de ecuaciones comprende a la ecuación de continuidad, las dos componentes de la ecuación de momentum y la ecuación de energía.

Para flujo incompresible, newtoniano y en estado no estacionario dichas ecuaciones, expresadas en notación diferencial- vectorial toman respectivamente la siguiente forma:

El último término de la ecuación de momentum en dirección vertical, ecuación (3), representa la fuerza volumétrica de flotación promotora del movimiento de convección natural, expresada mediante la aproximación de Boussinesq [2]. Por otra parte, el último término de la ecuación de energía (4) representa la rapidez de liberación de calor latente en la región pastosa. Para completar el modelo es necesaria una expresión matemática que relacione la fracción de sólido en dicha región con las variables principales del modelo. En teoría este parámetro debería ser calculado a partir de la modelación de la nucleación y el crecimiento dendrítico [1], sin embargo debido a la excesiva complejidad que ello supone, en la práctica se acuden a relaciones aproximadas. La relación más simple, la cual ha sido utilizada en el presente trabajo, es una relación lineal con la temperatura en el rango de solidificación [3]:

Las ecuaciones diferenciales (1)-(4) son válidas en todo el dominio ocupado por la fase líquida y en la región pastosa. En la fase sólida no existe movimiento y por tanto sólo es necesaria la ecuación de energía, que se reduce a la ecuación de conducción de calor, para modelar el proceso en esa región.

En la práctica, si las leves variaciones de las propiedades de la aleación respecto la temperatura son ignoradas y sólo son considerados valores medios, resulta más conveniente transformar las variables a la forma adimensional [5] usando como magnitudes de referencia la dimensión lineal L, la velocidad L, la presión p(L)² y el tiempo L²/, donde es la difusividad térmica. La temperatura usualmente es adimensionalizada en la forma θ = (T — T_F) I(T_C — T_F) , donde T_C y T_F son las temperaturas extremas durante el proceso de solidificación modelado. Con estas modificaciones las ecuaciones diferenciales adquieren la siguiente forma:

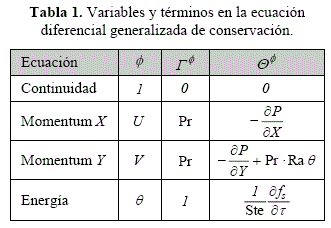
De esta forma se obtiene que todo el proceso de solidificación esta caracterizado por tres parámetros adimensionales: el número de Prandtl (Pr), el número de Rayleigh (Ra) y el número de Stefan (Ste). Con el fin de facilitar el posterior proceso de aproximación numérica, resulta ventajoso expresar todas las ecuaciones diferenciales anteriores como casos particulares de la ecuación generalizada de conservación:

Las variables y términos correspondientes a cada ecuación diferencial del modelo considerado se han resumido en la tabla 1.

 

3. FORMULACIÓN NUMÉRICA

3.1 DISCRETIZACIÓN DE LA ECUACIÓN GENERALIZADA

La solución numérica de las ecuaciones diferenciales que comprende el modelo matemático requiere como paso previo el proceso conocido como discretización, en el que dichas ecuaciones son aproximadas mediante sistemas de ecuaciones algebraicas que tienen como incógnitas a los valores de las variables en un conjunto de localizaciones discretas en el espacio y en el tiempo. El proceso de discretización descrito a continuación sigue los lineamientos del método de los volúmenes finitos.

Considérese un dominio bidimensional rectangular semejante al mostrado en la figura 1, en el cual es válida la ecuación generalizada de conservación (10). El fraccionamiento de este dominio en un conjunto de volúmenes de control de sección rectangular conduce a la formación de una retícula estructurada que define la ubicación de los puntos donde serán determinados valores discretos de la solución aproximada de la ecuación diferencial, puntos denominados nodos computacionales. En la figura 2 se muestra un volumen de control típico junto con la notación usualmente empleada para nombrar los nodos adyacentes a un volumen.

El paso inicial en el proceso de discretización descrito es la integración de los términos de la ecuación (10) en un volumen de control (V.C.) genérico:

Cada una de las integrales deben ahora aproximarse numéricamente, sin embargo, previamente es conveniente transformar las integrales de volumen de los términos convectivo y difusivo en integrales de superficie aplicando el teorema de la divergencia de Gauss [2], en la siguiente forma:

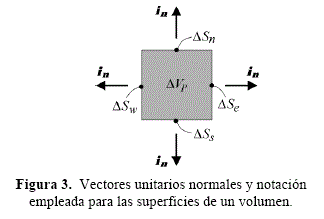
La superficie de control (S.C.) del volumen genérico de magnitud ΔV_P está compuesta a su vez por cuatro superficies (ΔS_e, ΔS_w, ΔS_n y ΔS_S) , en las cuales el vector unitario normal i_n está orientado tal como se muestra en la figura 3.

La aplicación de la regla del punto medio [2] para aproximar numéricamente el valor de cada una de las integrales presentes en la ecuación (12), conduce a las expresiones siguientes:

Las componentes de velocidad en la ecuación (14) se han denotado con asterisco porque sus valores exactos no son conocidos a priori y por ello deben utilizarse valores aproximados provenientes de iteraciones anteriores, durante el proceso secuencial de resolución de los sistemas de ecuaciones discretizadas.

El objetivo final del proceso es la obtención de una ecuación algebraica genérica expresada solamente en función de los valores de la variable principal <fi en los nodos de la retícula. Para ello es necesario emplear relaciones de interpolación para los valores en otros puntos y expresiones en diferencias finitas para las derivadas. Considerando como ejemplo la interpolación para el punto medio de la superficie e, ésta se puede expresar matemáticamente en la forma:

Existen varias alternativas para la elección del factor de interpolación X_e más adecuado. Desde el punto de vista de la estabilidad del proceso de solución numérica, la forma más conveniente corresponde a la interpolación UDS, la cual sin embargo introduce en la solución numérica errores de discretización de tipo disipativo [4]. El factor de interpolación para este caso depende de la dirección local del flujo y puede ser expresado en la forma:

Un esquema de interpolación alternativo que origina errores de discretización de menor magnitud en la solución numérica es el esquema CDS, el cual es equivalente a la interpolación lineal. El factor de interpolación para este esquema sólo depende de la posición relativa de los puntos considerados:

En un proceso de solución secuencial como el que será utilizado para resolver los sistemas de ecuaciones algebraicas es conveniente combinar la estabilidad del esquema UDS con la mayor exactitud del esquema CDS. Una forma de conseguir aquello es mediante la técnica conocida como corrección diferida [2], la cual puede expresarse mediante una relación de interpolación de la siguiente forma:

El término de corrección diferida, el cual sólo depende de valores nodales de iteraciones anteriores, está dado por:

La derivada temporal que aparece en la ecuación (13) puede ser aproximada mediante una expresión de primer orden en diferencias finitas:

El uso de este tipo de aproximación conduce a una formulación numérica incondicionalmente estable [4]. En cuanto a las derivadas espaciales necesarias para la ecuación (15), éstas pueden ser aproximadas mediante expresiones del tipo:

La sustitución de todas las aproximaciones numéricas indicadas en la ecuación (12) y la posterior agrupación de términos conducen a la siguiente forma final para la discretización de la ecuación generalizada, empleando la notación para los nodos mostrada en la figura 2:

Los coeficientes y el término independiente quedan definidos por las expresiones siguientes:

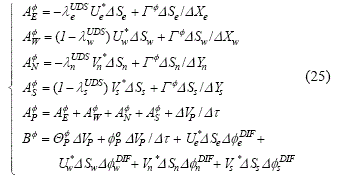
3.2 ECUACIÓN EVOLUTIVA PARA LA PRESION

El proceso de discretización descrito en la sección anterior es aplicable tanto a las dos componentes de la ecuación de momentum como a la ecuación de energía. Producto de esa operación es posible obtener para cada ecuación diferencial un sistema de ecuaciones algebraicas, el cual puede ser empleado para obtener a su vez, mediante un proceso iterativo de solución, un conjunto de tantos valores nodales de los campos de velocidad y temperatura como volúmenes de control se hayan considerado en la retícula.

La ecuación de continuidad merece un tratamiento especial, puesto que, al no presentar ninguna variable dominante, sólo puede ser utilizada para calcular el campo de presión, transformándola en una ecuación evolutiva para esta variable. Para tal efecto, considérese la integración de la ecuación de continuidad a través de un volumen de control genérico, transformando luego la integral de volumen en una integral de superficie:

La aproximación de la integral de superficie mediante la regla del punto medio permite obtener la ecuación:

Es posible emplear las ecuaciones discretizadas de momentum para expresar las componentes de velocidad en función de la presión, para así transformar la anterior ecuación en otra con la presión como variable principal. Por ejemplo, para el caso de la componente horizontal de velocidad, la ecuación discretizada de momentum X puede rescribirse en la siguiente forma:

La notación SPISX se ha utilizado para representar la aproximación de diferencias finitas de la derivada de presión. El término _P es denominado comúnmente como pseudo-velocidad y reúne a todos los términos no incluidos directamente en la ecuación, es decir:

La ecuación (28) y una ecuación equivalente para la componente vertical de velocidad podrían ser reemplazadas en la ecuación (27) para transformarla en una ecuación para la presión, sin embargo, existe la dificultad de que son necesarias las componentes de velocidad en los puntos medios de las superficies del volumen genérico y no en localizaciones nodales. Para subsanar dicho inconveniente, es posible considerar la existencia de volúmenes de control intermedios, para los cuales podrían obtenerse ecuaciones equivalentes a la ecuación (28). Por ejemplo, para un volumen alrededor del punto medio de la superficie e, tal como el mostrado en la figura 4, se podría obtener una ecuación discretizada de momentum en dirección horizontal de la forma:

Con el fin de evitar la repetición del cálculo de coeficientes para los volúmenes intermedios ficticios es posible realizar la interpolación de las ecuaciones discretizadas en los volúmenes originales y de ahí obtener todos los parámetros necesarios. Un esquema de interpolación que garantiza la satisfacción simultánea de las ecuaciones de continuidad y de momentum en los volúmenes de la retícula puede ser definido, para la pseudo-velocidad U_e y el término dependiente del coeficiente central (A_p^U)_e necesarios para la ecuación (30), en siguiente forma:

La sustitución de la ecuación (30) y relaciones semejantes en la ecuación (27) proporciona, después de un reordenamiento de términos, la siguiente ecuación evolutiva para presión:

Las relaciones matemáticas para el cálculo de los coeficientes y el término independiente de la anterior ecuación son las siguientes:

3.3 ALGORITMO DE SOLUCIÓN

El conjunto de sistemas de ecuaciones lineales obtenidas mediante el proceso de discretización debe ser resuelto en forma iterativa debido a la no linealidad y al complejo acoplamiento de variables de las ecuaciones diferenciales originales. El algoritmo de solución secuencial que ha sido empleado en conjunción con la formulación descrita en los apartados precedentes es el algoritmo PRIME (Pressure Implicit, Momentum Explicit) [4], el cual ha sido adaptado para la obtención de simulaciones numéricas en problemas de solidificación y se describe brevemente a continuación. Conocidos los valores nodales para los campos iniciales de U, V, P y T en = 0, los pasos principales del algoritmo propuesto son los siguientes:

1.   Son estimados los valores nodales de U y V en = + Δ.

2.   Con los valores actuales del campo de temperatura se identifican las regiones del dominio que son ocupadas por las fases líquida y sólida y por la región pastosa.

3.   Son calculados los coeficientes de las componentes X e Y de la ecuación de momentum en el dominio ocupado por la fase líquida y la región pastosa.

4.   Son calculadas las pseudo-velocidades y en los puntos nodales, con ecuaciones análogas a la ecuación (29), y luego son interpolados los valores necesarios en los puntos medios de las superficies de los volúmenes, con ecuaciones semejantes a las ecuaciones (31) y (32).

5.   Los coeficientes de la ecuación evolutiva de presión son calculados a través de las ecuaciones (34) y es resuelto el sistema lineal de ecuaciones resultante.

6.   Los valores nodales de U y V son corregidos con expresiones análogas a la ecuación (28). Con los nuevos valores se retorna al paso 4 y se itera un cierto número de veces.

7.   Son calculados valores de la fracción de sólido en la región pastosa a través de la ecuación (5).

8.   Son calculados los coeficientes de la ecuación de energía y es resuelto el sistema lineal resultante. En la zona ocupada por la fase sólida las componentes de velocidad son consideradas nulas.

9.   Se retorna al paso 2 y se repite toda la secuencia de pasos hasta alcanzar el nivel de convergencia requerido en todos los campos. En este punto se ha obtenido la solución en = +Δ .

10. Se avanza un nuevo intervalo de tiempo y todos los pasos son nuevamente repetidos.

Para la resolución de los sistemas lineales de ecuaciones en los pasos 5 y 8 se ha empleado el método iterativo Gauss-Seidel punto por punto [4].

 

4. EJEMPLO DE APLICACIÓN

En la figura 5 se muestra esquemáticamente un problema de solidificación empleado para ejemplificar la aplicación de la formulación presentada. En una cavidad de sección cuadrada se encuentra en = 0 una aleación en reposo a la temperatura θ = 1, ocupando la fase líquida todo el dominio. Las paredes superior, inferior e izquierda de la cavidad se suponen aisladas térmicamente, mientras que la pared derecha se encuentra sometida a la temperatura adimensional uniforme θ = . Se ha prescrito que el cambio de fase en la aleación ocurre en el intervalo definido por las temperaturas adimensionales θ_SOl = 0.3 y θ_liq = 0.5.

Para la simulación presentada se especificaron los siguientes valores para los parámetros adimensionales: número de Rayleigh Ra = 10 , número de Prandtl Pr = 0.01 y número de Stefan Ste = 1. Para la solución numérica del problema se utilizó una retícula uniforme de 80 x 80 volúmenes de control y un intervalo de tiempo adimensional Δ = 0.001. El proceso iterativo de solución se realizó siguiendo los lineamientos descritos en la sección 3.3, a través de una aplicación computacional programada en forma específica para la solución del problema tratado y ejecutada en un computador personal con procesador Pentium de 233 MHz con entorno operativo Windows.

En la figuras 6a-d y 7a-d son mostradas gráficas correspondientes a ocho etapas de la simulación obtenida para el problema de solidificación tratado en el ejemplo. Las gráficas muestran la evolución del proceso a través de la representación de las líneas de corriente del flujo en la fase líquida y la región pastosa, las líneas de valor constante del campo de temperatura y el crecimiento de la fase sólida y de la región pastosa. Las líneas de corriente se han obtenido mediante la obtención de valores de la denominada función de corriente [6], a partir de los valores determinados para el campo de velocidad. La cantidad de fluido en movimiento entre líneas de corriente adyacentes es la misma para todas las gráficas.

En las etapas iniciales del proceso mostradas en la figura 6, puede apreciarse claramente la fuerte influencia del movimiento de convección natural que se produce en la fase líquida y la región pastosa sobre la configuración del campo de temperatura y por tanto sobre la distribución de las zonas ocupadas por las fases. Además de una zona principal de flujo en la que el fluido circula cuasi-concéntricamente, es posible observar la presencia de zonas con flujos circulantes secundarios en la proximidad de los vértices de la cavidad. Asimismo, existe una clara tendencia de las líneas de corriente a agruparse en la periferia de la zona principal de flujo dejando en el núcleo una región con fluido cuasi-estático. Por otra parte, el crecimiento de la fase sólida es inicialmente muy lento, a diferencia del crecimiento de la región pastosa que rápidamente desaloja a la fase líquida y pasa a ocupar la mayor parte del dominio.

A medida que avanza el tiempo y decrece la zona donde existe movimiento promovido por convección natural, la influencia de éste sobre la marcha del proceso se reduce. En las gráficas de las líneas de corriente de la figura 7 se observa una progresiva disminución en la cantidad de éstas, hecho que indica la reducción gradual en la velocidad del movimiento. Asimismo es posible observar un crecimiento en la zona ocupada por los flujos recirculantes secundarios en la parte superior del dominio, los cuales sufren constantes cambios en su configuración y ubicación relativa a medida que avanza el tiempo. En la simulación presentada, el proceso completo de solidificación, desde el inicio hasta el instante en que la fase sólida llega a ocupar todo el dominio de solución, comprendió un intervalo total de 1.41 en tiempo adimensional.

 

5. CONCLUSIONES

Una formulación numérica para la simulación de procesos de solidificación de aleaciones ha sido presentada y evaluada mediante un ejemplo de aplicación. La formulación presenta un grado de simplicidad tal que ha sido posible su implementación en un computador personal de reducida capacidad. Los resultados de las simulaciones son comparables a los obtenidos mediante el empleo de otras metodologías más elaboradas y complejas [3][5].

Sin embargo, a pesar del significado alentador de los resultados obtenidos, varios aspectos de la formulación presentada pueden ser mejorados en el futuro. Por ejemplo, el flujo en la región pastosa es semejante en muchos aspectos al flujo en un medio poroso y su modelación como tal significaría una mayor aproximación con la realidad. Por otra parte, en el ejemplo presentado, las ecuaciones de momentum y continuidad fueron resueltas considerando la frontera entre la fase sólida y la región pastosa como una curva irregular acomodada a la retícula, el tratamiento de esta frontera como una curva continua proporcionaría resultados más realistas aún. Una otra alternativa de mejora sería la utilización de propiedades de aleaciones específicas mediante la inclusión de correlaciones empíricas para la variación con la temperatura de dichas propiedades y de la fracción de sólido en la región pastosa.

 

REFERENCIAS BIBLIOGRÁFICAS

[1] Duff E. S. Fluid flow aspects of solidification modeling: simulation of low pressure die casting. Ph.D. Thesis. Department of Mining and Metallurgical Engineering, University of Queensland, Australia. 1999.        [ Links ]

[2] Ferziger J. H., Peric, M. Computational methods for fluid flow dynamics. Springer-Verlag. 1996.        [ Links ]

[3] Lewis R. W., Ravidran K. Finite element simulation of metal casting. International Journal for Numerical Methods in Engineering. Vol. 47, 29-59. 2000.        [ Links ]

[4] Maliska C. R. Transferência de calor e mecânica dos fluidos computacional. Livros Técnicos e Científicos Editora S.A. Rio de Janeiro. 1995.        [ Links ]

[5] Nithiarasu P. An adaptive finite element procedure for solidification problems. Heat and Mass Transfer. Vol. 36, 223-229. 2000.        [ Links ]

[6] Velasco F. Formulación de volúmenes finitos para la simulación de flujo compresible bidimensional en estado estacionario. Tesis de Graduación. Carrera de Ingeniería Mecánica. Universidad Técnica de Oruro, Bolivia. 2000.        [ Links ]