Services on Demand
Article
Indicators
Related links
 Cited by SciELO
Cited by SciELO
 Similars in SciELO
Similars in SciELO
Bookmark
Reporte Metalurgico y de Materiales
Print version ISSN 2010-0407
Reporte Metalurgico y de Materiales no.7 La Paz Apr. 2010
ARTICULO
MODELO PARA ESFUERZO DE CEDENCIA DE PULPAS DE CUARZO Y RELAVES DE COBRE
Bonifacio Alejo"', Arturo Barrientos ,
a Instituto de Investigaciones Metalúrgicas y Materiales, Universidad Mayor de San Andrés, Avenida Las Américas No. 100, Villa Fátima, La Paz, Bolivia
Departamento de Ingeniería Metalúrgica, Universidad de Concepción, Edmundo Larenas No. 285, Concepción, Chile
Resumen
El modelo de esfuerzo de cedencia basado sobre el concepto de grados de libertad de un sistema particulado en medio acuoso ha sido validado experimentalmente con suspensiones de cuarzo de concentraciones de ![]()
El tamaño de las partículas de cada suspensión involucrado en el modelo ha sido corroborado exitosamente con módulos de tamaño de Rosin Rammler de ![]() =11 a 46 micrones. Ha sido exitosamente aplicado con éxito a una suspensión de relaves de cobre de la Gran Minería del Cobre chilena. El modelo involucra la máxima fracción de empaquetamiento
=11 a 46 micrones. Ha sido exitosamente aplicado con éxito a una suspensión de relaves de cobre de la Gran Minería del Cobre chilena. El modelo involucra la máxima fracción de empaquetamiento ![]() ,parámetro muy importante relacionado con la interacción entre las partículas que forman la suspensión. Las suspensiones de partículas finas reportan valores de empaquetamiento de baja densidad en relación a los tamaños gruesos. Las concentraciones cercanas al empaquetamiento máximo (
,parámetro muy importante relacionado con la interacción entre las partículas que forman la suspensión. Las suspensiones de partículas finas reportan valores de empaquetamiento de baja densidad en relación a los tamaños gruesos. Las concentraciones cercanas al empaquetamiento máximo (![]() ), conllevan a valores de esfuerzo de cedencia muy altos.
), conllevan a valores de esfuerzo de cedencia muy altos.
El modelo es capaz de predecir la concentración crítica de sólidos en la descarga de un espesador industrial de colas relaves de cobre. La fracción máxima de empaquetamiento en la descarga del espesador es de ![]() =0.35.
=0.35.
1. Introducción
El esfuerzo de cedencia es uno de los parámetros reológicos de gran importancia en muchas suspensiones, ya sea en la industria alimenticia, productos farmacéuticos, pinturas, en la industria cerámica, como en caso particular de suspensiones minerales. La importancia de esfuerzo de cedencia en el campo de Procesamiento de Minerales está relacionada principalmente con la molienda (Klimpel, 1982;Ding et al., 2007) y el espesamiento de concentrados o relaves.
En la literatura (Subbanna et al. 1998; Johnson et al. 2000), se establece que el esfuerzo de cedencia está relacionado con la estructura interna de la suspensión. Para que esta estructura comience a fluir es necesario vencer el esfuerzo cortante mínimo necesario para romper el contacto interpartícula y las uniones de los agregados ó flóculos. Esta estructura está formada por partículas, cuyas cargas eléctricas son de signos contrarios (punto isoeléctrico).
La fuerza de atracción interpartícula de esta estructura es del tipo de Van der Waals. Las variables de influencia sobre el esfuerzo de cedencia son, la concentración de sólidos, el tamaño de las partículas, la forma, el pH y la naturaleza del material. Al igual que la concentración de sólidos, el parámetro de mucha influencia es el tamaño de las partículas. La presencia de partículas finas pueden exhibir diversos fenómenos reológicos, como el cizalle adelgazante, cizalle espesante, formación de cedencia y tixotropía entre otros (Willdemutth et al. 1985; Dabak et al. 1987). El movimiento Browniano de las partículas es fuertemente dependiente del tamaño y viene a ser notable con tamaños de partículas más pequeños, menores a 1 micrón (Makosco, 1994; Zhou et al. 2001). En cambio, el pH del medio viene a jugar un rol muy importante con minerales oxidados, especialmente en el punto isoeléctrico de la curva de potencial zeta (iep) de la partícula, lugar de la máxima formación de flóculos o agregados, debido a las fuerzas atractivas de Van der Waals, y la suspensión en este punto desarrolla la máxima viscosidad de cizalle.
La modificación de las propiedades superficiales de las partículas para la estabilidad de las suspensiones puede ser conseguida a través de varios mecanismos. Entre otros, está en regiones donde predominan las fuerzas repulsivas, esto es, a pHs lejos del punto isoeléctrico de la partícula. En los trabajos de Subbanna et al. (1998), Gustafsson et al. (2003) y Liang et al. (2005) han investigado el rol del parámetro punto isoeléctrico en el comportamiento reológico de suspensiones de óxidos de titanio, zirconio y alúmina.
El otro mecanismo de estabilización de una suspensión mineral es mediante la adición de reactivos llamados dispersantes. Dicha alteración superficial de las partículas conlleva a la estabilidad de la suspensión, y el comportamiento de la suspensión tiende a ser de un fluido newtoniano. Por tanto, el estudio de la estabilidad reológica de las suspensiones requiere de un conocimiento del rol de las fuerzas interpartículas sobre el comportamiento reológico de las suspensiones para predecir y controlar las propiedades de la suspensión.
El propósito de este trabajo es estudiar el efecto de las principales variables de la reología de suspensiones, la concentración de sólidos y el tamaño de la partícula a través de un nuevo modelo de esfuerzo de cedencia con suspensiones de cuarzo y colas relaves de cobre de Codelco Norte en medio acuoso.
2. Ecuaciones de movimiento
Las ecuaciones de movimiento, en ausencia de reacciones químicas, efectos térmicos y electromagnéticos, están dadas por los balances locales de conservación de masa y de momentum. Considerando el flujo permanente de un fluido incompresible, las ecuaciones que describen el fenómeno, despreciando los efectos inerciales, están dadas por (Concha y Barrientos, 1993):

La ecuación constitutiva del tensor de esfuerzos T para los fluidos con comportamiento no Newtoniano está dada por la subclase de fluidos de Reinar-Rivlin. Para suspensiones concentradas de sólidos en fluidos, polímeros y soluciones de pequeñas porciones de polímeros en un líquido, la ecuación constitutiva de Fluido Newtoniano Generalizado, esta expresada por:
![]()
La expresión más general de una relación escalar de la ecuación constitutiva para un fluido no-Newtoniano, es desarrollada aprovechando la propiedad de que la traza de un tensor simétrico es invariante. Tomando el tensor esfuerzo extra de la ecuación (3) de un Fluido Newtoniano Generalizado,
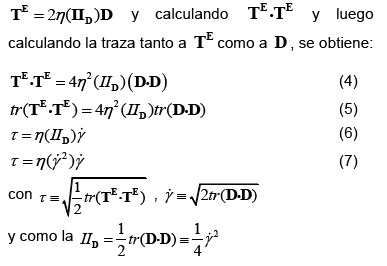
Existen muchos modelos de fluidos no Newtonianos, algunos de ellos para flujos de cizalle simple están citados en la Tabla 1.

2.1. Formulación del modelo de esfuerzo de cedencia
La concentración de sólidos expresado en fracción de volumen de sólidos,![]() , es una de las variables fundamentales de la reología de suspensiones, y cuya definición está dada localmente por:
, es una de las variables fundamentales de la reología de suspensiones, y cuya definición está dada localmente por:

En el manejo de suspensiones, la concentración de sólidos puede variar en un amplio rango de contenido de sólidos, desde diluidas, pasando por las moderadas, hasta las más concentradas cercanas a las diferentes configuraciones de pseudo cristal (Quemada et al. 2002).
En suspensiones diluidas, las partículas pueden moverse libremente en todo el espacio disponible, donde predomina el movimiento Browniano de rotación y traslación. Existe una gran distancia media de separación entre las partículas comparadas con el tamaño medio de la partícula, donde el movimiento es lento, la energía cinética de las partículas sólidas es despreciable; no hay deslizamiento del líquido relativo a la superficie de la partícula; la densidad de las partículas es igual a la del medio continuo, a fin de que no haya efectos de sedimentación. Bajo esta hipótesis, Einstein (1956) derivó su famosa ecuación para la viscosidad de una suspensión.
En otro estado más denso, las partículas cada vez tienen menos espacio disponible para moverse, la distancia media de separación partícula-partícula se reduce notablemente con el aumento de número de partículas. La interacción partícula-partícula es notable. El medio líquido y las partículas pueden formar estructuras que dependen de las fuerzas coloidales predominantes. Las partículas con cargas eléctricas iguales tienden a separarse debido a las fuerzas repulsivas, formando así una estructura de una pseudo red cristalina (Barnes, 1989).
En cambio, las estructuras de agregados o flóculos conducen a empaquetamientos de baja densidad (![]() ). En general, los flóculos o agregados no seacercan al empaquetamiento compacto de un pseudocristal. El esfuerzo requerido para romper esta estructura mencionada tiene valores altos. Las variables que influyen fuertemente sobre este parámetro de empaquetamiento (
). En general, los flóculos o agregados no seacercan al empaquetamiento compacto de un pseudocristal. El esfuerzo requerido para romper esta estructura mencionada tiene valores altos. Las variables que influyen fuertemente sobre este parámetro de empaquetamiento (![]() ) son la concentración de sólidos, el tamaño de la partícula y la forma de las partículas (Chang et al. 2002).
) son la concentración de sólidos, el tamaño de la partícula y la forma de las partículas (Chang et al. 2002).
Existen muchos modelos que involucran el parámetro (![]() ) en la formulación de esfuerzo de cedencia (Willdemuht y Williams, 1985), mientras otros lo hacen mediante el análisis adimensional (Dabak y Yucel, 1987). Si analizamos una partícula encerrada en un recinto de dimensiones
) en la formulación de esfuerzo de cedencia (Willdemuht y Williams, 1985), mientras otros lo hacen mediante el análisis adimensional (Dabak y Yucel, 1987). Si analizamos una partícula encerrada en un recinto de dimensiones ![]() (fracción deempaquetamiento), esta puede moverse en él libremente.
(fracción deempaquetamiento), esta puede moverse en él libremente.
El movimiento de la partícula está caracterizado a través de su posición r y de su velocidad v. Por tanto, esta partícula tiene 6 grados de libertad para su movimiento (las tres coordenadas y las tres componentes del campo de velocidades). Sin embargo, para algunos casos de interés, esta partícula puede sufrir varias restricciones tanto sobre su posición como sobre su velocidad. Una restricción puede ser, por ejemplo, que la partícula pueda moverse en una sola dirección; en este caso, la partícula tiene solamente dos grados de libertad. En general, para un sistema formado por N partículas tendrá 6 N grados de libertad. Al igual que para el caso de una sola partícula, un sistema de partículas también está sujeto a restricciones sobre su movimiento.
Para este último caso, al aumentar el número de partículas, el espacio disponible para cada partícula se verá disminuido considerablemente (disminución de los grados de libertad de cada partícula) y puede llegar a una situación donde el espacio disponible se reduzca hasta que las partículas lleguen a tocarse superficie con superficie, formando así un empaquetamiento de partículas ![]() Por tanto, es fácil deducir, la viscosidad de esta suspensión con una concentración cercana al empaquetamiento máximo tiene un valor muy grande
Por tanto, es fácil deducir, la viscosidad de esta suspensión con una concentración cercana al empaquetamiento máximo tiene un valor muy grande ![]()
En consecuencia, es razonable asumir que, el espacio disponible para cada partícula se puede definir como la diferencia entre una concentración cualquiera ![]() y la fracción máxima de empaquetamiento,
y la fracción máxima de empaquetamiento,![]() esto es,
esto es,![]() . Esta diferencia disminuye con el aumento del número de partículas y la interacción partícula-partícula aumenta inversamente sobre el esfuerzo de cadencia (
. Esta diferencia disminuye con el aumento del número de partículas y la interacción partícula-partícula aumenta inversamente sobre el esfuerzo de cadencia (![]() ).
).
Por tanto, es razonable deducir que el esfuerzo de cedencia es inversamente proporcional al espacio disponible de la partícula, esto es:

donde,![]() es la fracción máxima de empaquetamiento o máxima densidad de empaquetamiento.
es la fracción máxima de empaquetamiento o máxima densidad de empaquetamiento.
Por otra parte, el tamaño de las partículas es otra variable fundamental de la reología de suspensiones. En el modelo empírico de Tangsathitkulchai y Austin (1988) y otras (Kapur et al., 1996; Flatt, 2006; Harbour et al., 2007) el esfuerzo de cedencia es inversamente proporcional al tamaño de las partículas.
Las partículas finas por su alta superficie específica generan una fuerte interacción partícula-partícula en medio acuoso, principalmente para el caso de los minerales oxidados. El esfuerzo necesario para separar el contacto interpartícula llega a ser muy grande, aún a bajo contenido de sólidos. Entonces, en base a estos conceptos señalados, se puede deducir que, el esfuerzo de cedencia es inversamente proporcional al tamaño de las partículas Lc , de la forma:

La formulación del modelo de esfuerzo de cedencia es obtenida a partir de la multiplicación de las ecuaciones (9), (10) y otras variables que influyen sobre el esfuerzo de cedencia que no han sido tomadas en cuenta. El esfuerzo de cedencia en función tanto de la concentración de sólidos como del tamaño de partículas, está dado por:
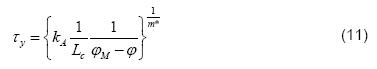
donde, kA es una constante de proporcionalidad,![]() es la fracción máxima de empaquetamiento de sólidos, Lc es la longitud característica de las partículas.
es la fracción máxima de empaquetamiento de sólidos, Lc es la longitud característica de las partículas.
En el presente trabajo, la longitud característica se toma el módulo de tamaño de Rosin Rammler (k) y m* es un parámetro de interacción de muchas variables.
Así, el modelo de esfuerzo de cedencia tiene tres parámetros (![]() ), que son obtenidos por ajuste no lineal de datos experimentales. El modelo de esfuerzo de cedencia para un sistema particulado en medio líquido está sujeto a las siguientes suposiciones:
), que son obtenidos por ajuste no lineal de datos experimentales. El modelo de esfuerzo de cedencia para un sistema particulado en medio líquido está sujeto a las siguientes suposiciones:
1) Las partículas de la suspensión son rígidas y de un tamaño característico Lc.
2) El modelo tiene validez para suspensiones de partículas sólidas con comportamiento reológico de un fluido no Newtoniano con esfuerzo de cedencia![]()
3) Se asume que las partículas generan interacción partícula-partícula en mayor o menor grado.
3.- Materiales y Métodos
La muestra de cuarzo de tamaño menor a 3 mm para las pruebas de mediciones de propiedades reológicas fue proporcionada por Codelco Norte de Chile. El análisis químico de la muestra está reportado en la Tabla 2.

El material de tamaño menor a 3 mm pulgadas fue molido en seco en un molino de bolas de acero de 7x9 pulgadas con medios de molienda de tamaño uniforme de una pulgada hasta obtener una distribución granulométrica de 100% -100 mallas Tyler (150 micrones).
El módulo de tamaño () fue determinado del análisis granulométrico para un acumulativo pasante de 63.21% en peso del material. El primer módulo de tamaño fue determinado del análisis granulométrico de un conjunto de material de 100% -100 mallas y se consideró la cantidad necesaria para un determinado número de pruebas. El resto del conjunto del material fue sometido a la molienda hasta conseguir el segundo módulo de tamaño, tomando la cantidad necesaria similar al primer módulo, con el resto se continuó en forma análoga para obtener los otros módulos de tamaño.
Los módulos de distribución de tamaño fueron determinados por ajuste no lineal de datos de análisis granulométrico mediante la ecuación empírica de Rosin - Rammler. Los pesos específicos del cuarzo y colas relaves de Codelco Norte fueron determinados por triplicado por el método del picnómetro, de valores de 2.55 y 2.87, respectivamente.
3.1.- Medición de tamaños
El análisis granulométrico de cada muestra fue realizado por difracción de rayos láser en húmedo en el analizador SYMPATEC HELOS. En él, las muestras fueron suspendidas en agua destilada en la celda Sucell dispersada con ultrasonido durante 10 segundos.
Cinco muestras de cuarzo fueron preparados con módulos de tamaño de la distribución granulométrica de Rosin-Rammler de k = 11, 15, 22, 36 y 46 micrones y con un módulo de distribución de tamaño de m=1.0. En la Fig. 1 se muestra las distribuciones granulométricas de las cinco muestras preparadas, incluyendo el material de colas relaves de Codelco Norte.
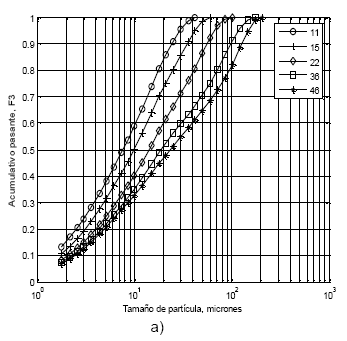
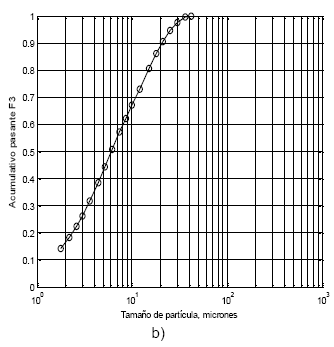
Fig. 1. Distribución granulométrica de las muestras con módulos de tamaño y distribución de a) Cuarzo de =11, 15, 22, 36 y 46 micrones y =1.0; y b) Colas relaves de k =9 y m =1.20.
La relación empírica utilizada para la distribución granulométrica es la de Rosin Rammler, dada por:

donde k es el módulo de tamaño y m es el módulo de distribución de tamaño.
Las suspensiones fueron preparadas en fracciones volumétricas de sólidos de ![]() = 0.25 a 0.51. El diseño de las pruebas experimentales se observa en la Tabla 3.
= 0.25 a 0.51. El diseño de las pruebas experimentales se observa en la Tabla 3.
El equipo de medición de la viscosidad consta de tres componentes principales, el viscosímetro Haake RV20N con sistema de medición ME, el rheocontroller RC-20 para el control del esfuerzo y la tasa de cizalle y un termostato para el control de la temperatura.
3.2.- Medición reológica
La geometría del viscosímetro Haake CV20N está constituida de dos cilindros concéntricos, el cilindro exterior (la cubeta) tiene un diámetro de 45 mm y gira a una velocidad angular ![]() . El cilindro interior está fijo y constituye el sensor de Mooney-Ewart (ME 45) de diámetro de 41.74 mm con altura de 36 mm. La abertura entre ambos cilindros es de 1.63 mm.
. El cilindro interior está fijo y constituye el sensor de Mooney-Ewart (ME 45) de diámetro de 41.74 mm con altura de 36 mm. La abertura entre ambos cilindros es de 1.63 mm.
Antes de la medición de la viscosidad, cada muestra de cuarzo de un peso determinado correspondiente a cada concentración fue acondicionada con un volumen determinado de solución de pH conocido en un vaso de precipitado de 100 ml.
La técnica de mojado de sólidos fue realizada manualmente hasta lograr el humedecimiento total. Después de tres horas, la muestra es transferida a la cubeta de medición de 10 ml, completando así la solución hasta la fracción de volumen deseada lista para la medición. Los reguladores de pH utilizados fueron ácido sulfúrico de densidad de 1.84g/cc y de pureza de 93-97%; e hidróxido de sodio de grado para análisis.
Las mediciones de viscosidad fueron realizadas a la temperatura de 20°C, mantenida constante mediante agua circulante del termostato. La medición fue controlada desde un PC para una concentración dada, en un rango de tasa de cizalle adecuado. Finalizada la medición, el pH de la suspensión es medido mediante un pHmetro digital HANNA INSTRUMENT.
La medición del pH de la suspensión se realiza antes y después de la medición de viscosidad. Este último valor es considerado como el pH de la suspensión.

4.- Resultados y Discusión
La carga superficial de las partículas de cuarzo en medio acuoso está controlada por la adsorción o disociación de iones y OH sobre los grupos silanos de la superficie como sitios positivos de acuerdo a la reacción![]() y como sitios negativos
y como sitios negativos ![]() . Lugar donde estas cargas son iguales es a pH 2.0 (i.e.p) para el cuarzo puro. Los resultados experimentales de la Fig. 2 a pH 7.0 muestran cuatro curvas de flujo a las concentraciones
. Lugar donde estas cargas son iguales es a pH 2.0 (i.e.p) para el cuarzo puro. Los resultados experimentales de la Fig. 2 a pH 7.0 muestran cuatro curvas de flujo a las concentraciones ![]() = 0.40, 0.45, 0.50 y 0.51,
= 0.40, 0.45, 0.50 y 0.51,
todas ellas exhiben esfuerzo de cedencia a este pH (lejos del punto isoeléctrico), y corresponden al comportamiento de un fluido no-Newtoniano.
En cambio, con óxidos de titanio, TiO2, alúmina, A12O3 o zirconio, ZrO2 (Liang, 2005; Gou et al. 2003), el comportamiento corresponde de un fluido Newtoniano lejos del pH de punto isoeléctrico de la curva de potencial zeta. El cuarzo estudiado en medio acuoso no sigue el mismo comportamiento de los óxidos mencionados (a pH lejos del punto isoeléctrico), esta influencia del medio sobre la superficie de las partículas de cuarzo puede ser atribuida a la adsorción de otras especies presentes, orgánicas e inorgánicas disueltas.
Entre las principales especies atribuidas son las de hierro, éstas pueden existir en grupos, simple, doble o triple coordinación de la superficie ![]() , que influyen significativamente en la carga y la reactividad de las caras cristalográficas, como ha sido demostrado con hematita (Addai-Mensah et al. 2004; Tombaczet al. 2001).
, que influyen significativamente en la carga y la reactividad de las caras cristalográficas, como ha sido demostrado con hematita (Addai-Mensah et al. 2004; Tombaczet al. 2001).
Las principales fuentes de especies de hierro, pueden ser atribuidas al mismo mineral de cuarzo como portadora de impurezas. Según estudios (Hauptkorna et al. 1997) utilizando la técnica de espectroscopía de masas por plasma se cuantificó 14 elementos en cuarzo de una pureza 99.9%, entre ellos están como especies mayoritarios el Al seguido de Fe. Y la otra fuente puede ser atribuida a la molienda en solera y con bolas de acero. Por tanto, la presencia de las especies coloidales de hierro y las especies orgánicas e inorgánicas disueltas, impactan significativamente sobre la química interfacial de la pulpa (potencial zeta).
Así, el esfuerzo de cedencia de la suspensión corresponde a las especies de hierro adsorbidas sobre las partículas de cuarzo. En la Fig. 3 se observa esquemáticamente la adsorción de estas especies sobre la partícula de cuarzo y la formación de agregados por fuerzas de atracción de Van der Waals. Los puntos isoeléctricos de estas especies [hematita (![]() ), magnetita (
), magnetita (![]() ), goetita (
), goetita (![]() ), lepidocrocita (
), lepidocrocita (![]() )] van de pH 5 a pH 9 (Addai-Mensah et al. 2004).
)] van de pH 5 a pH 9 (Addai-Mensah et al. 2004).
Las propiedades reológicas de las suspensiones de cuarzo determinadas mediante mediciones en el viscosímetro Mooney-Ewart están ilustradas en las curvas de flujo de la Fig. 2.
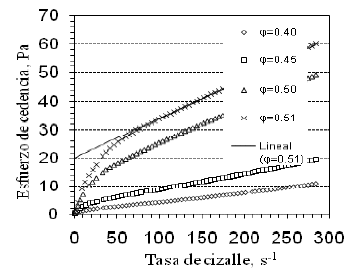
Fig. 2. Curva de flujo suspensiones de cuarzo. Condiciones: pH=7.0, con módulos de tamaño y distribución de = 46 micrones y de =1.0. Conparámetros de Bingham ![]() 20.0 Pa,
20.0 Pa, ![]() =0.1396 Pa.s, y con R2 =0.9525.
=0.1396 Pa.s, y con R2 =0.9525.
Como se esperó, es relevante observar el fenómeno de deslizamiento de las paredes del sensor de medición en la región de tasa de cizalle de ![]() . Por tanto, el esfuerzo de cedencia de cada una de las suspensiones al igual que en otros trabajos (Huynh et al., 2000) fue obtenido por extrapolación en la región de plástico de Bingham a tasa de cizalle cero (
. Por tanto, el esfuerzo de cedencia de cada una de las suspensiones al igual que en otros trabajos (Huynh et al., 2000) fue obtenido por extrapolación en la región de plástico de Bingham a tasa de cizalle cero (![]() ).
).
El fenómeno de deslizamiento han sido estudiados por Nguyen y Boger (1998) y Walls et al. (2003) con otras geometrías, como los viscosímetros capilares, cilindros concéntricos, cono/plato y plato/plato, respectivamente. Según estudios recientes, se ha demostrado que hay otros diseños que eliminan por completo este fenómeno (Zhou et al. 2001; Kee et al. 2007).
4.1.- Efecto de la concentración de sólidos![]() sobre
sobre ![]()
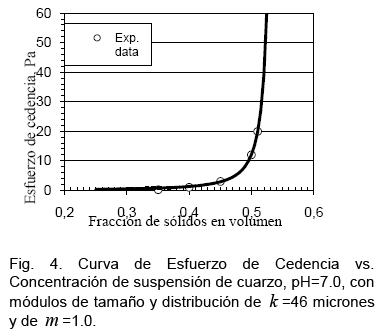
Los parámetros involucrados en el modelo de esfuerzo de cedencia propuesto (ecuación 11) como función de la concentración de sólidos y del tamaño de partículas, fueron evaluados mediante datos experimentales de suspensiones de cuarzo. En la Fig. 4 se muestra el mejor ajuste no lineal del modelo para una suspensión de tamaño de partículas de k = 46 micrones, los parámetros encontrados son:
![]()
Tal como se aguardó, existe una buena predicción del esfuerzo de cedencia en el rango de contenido de sólidos estudiado de ![]() =0.35 a 0.51. La fuerte interacción partícula-partícula se ve reflejada con altos contenidos de sólidos. La máxima fracción de empaquetamiento de la suspensión estudiada es
=0.35 a 0.51. La fuerte interacción partícula-partícula se ve reflejada con altos contenidos de sólidos. La máxima fracción de empaquetamiento de la suspensión estudiada es ![]() =0.542. Para concentraciones cercanas a este parámetro (menor espacio para moverse), el esfuerzo de cedencia adquiere valore muy altos. A modo de ejemplo, para una concentración de sólidos de
=0.542. Para concentraciones cercanas a este parámetro (menor espacio para moverse), el esfuerzo de cedencia adquiere valore muy altos. A modo de ejemplo, para una concentración de sólidos de![]() =0.51, el valor de
=0.51, el valor de ![]() es 19.78 Pa
es 19.78 Pa
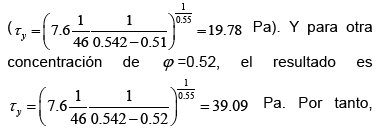
con pequeñas adiciones de partículas, la fluidez de la suspensión disminuye notablemente hasta situarse en la región de pastas (Nguyen y Boger, 1998).
4.2. Efecto del tamaño de partículas sobre ![]()
El modelo propuesto permite predecir el efecto del tamaño de partículas representado por el módulo de distribución natural de Rosin Rammler de ![]() =1.0 de una suspensión de cuarzo sobre el esfuerzo de cedencia. El efecto del tamaño sobre el
=1.0 de una suspensión de cuarzo sobre el esfuerzo de cedencia. El efecto del tamaño sobre el![]() para las suspensiones de tamaños de k=11 a 46 micrones se muestra en la Fig. 5. Los parámetros del modelo de esfuerzo de cedencia encontrados por ajuste no lineal se muestran en la tabla 4. Los resultados muestran una fuerte influencia del tamaño sobre el esfuerzo de cedencia, especialmente con los finos k=11 y 15 micrones.
para las suspensiones de tamaños de k=11 a 46 micrones se muestra en la Fig. 5. Los parámetros del modelo de esfuerzo de cedencia encontrados por ajuste no lineal se muestran en la tabla 4. Los resultados muestran una fuerte influencia del tamaño sobre el esfuerzo de cedencia, especialmente con los finos k=11 y 15 micrones.
Esto corrobora la fuerte interacción partícula-partícula para formar flóculos o agregados de baja densidad de empaquetamiento, por que la formación de cadenas o redes de partículas reduce la fluidez de la suspensión. Para que la suspensión fluya un mayor esfuerzo es necesario para romper la red de partículas del empaquetamiento como el que esta mostrado en la Fig. 6a).
En esta figura se observa un estado de red de empaquetamiento de partículas muy voluminoso, parecido a una "esponja". Por el contrario, en el otro caso, hay una dispersión de partículas en forma ordenada debido a las fuerzas hidrodinámicas o a las fuerzas de repulsión, donde el contacto entre las partículas es muy reducido, es de esperar que el esfuerzo de cedencia tenga valores pequeños (ver Fig. 6b)
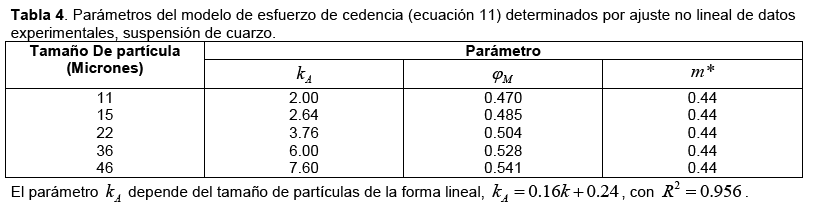
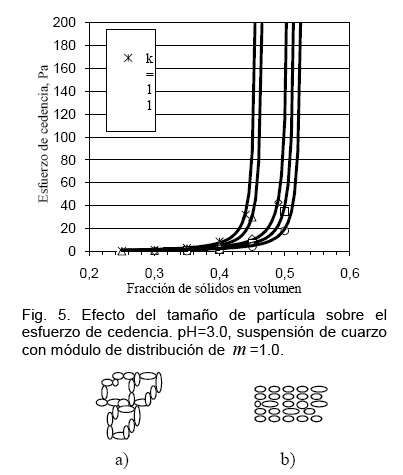
Fig. 6. Configuraciones de máxima fracción de empaquetamiento, a) partículas de carga opuesta formando redes de contacto partícula-partícula (flóculos o agregados) debido a las fuerzas de atracción de Van der Waals, b) partículas dispersas debidas a las fuerzas hidrodinámicas ó fuerzas de repulsión.
4.3.- Validación del modelo con relaves de mineral de cobre
El modelo propuesto fue extendido para predecir el esfuerzo de cedencia de sistemas reales, como es la suspensión de relaves de mineral de cobre de Codelco-Norte.
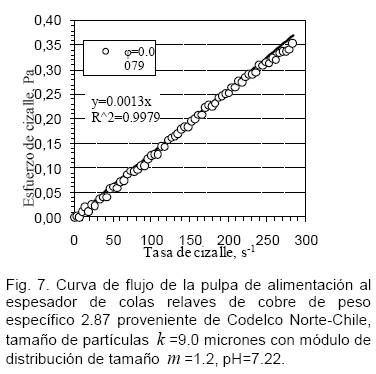
En la Fig. 7 se muestra la caracterización reológica de la pulpa de alimentación al espesador de colas relaves de cobre. De acuerdo a la curva de flujo, el comportamiento de la suspensión corresponde de un fluido Newtoniano con un viscosidad constante de 1.3 ![]() . Las mediciones reológicas de las concentraciones de sólidos de
. Las mediciones reológicas de las concentraciones de sólidos de ![]() =0.10 a 0.30 han sido obtenidas por espesado a partir de la concentración
=0.10 a 0.30 han sido obtenidas por espesado a partir de la concentración![]() =0.0079.
=0.0079.
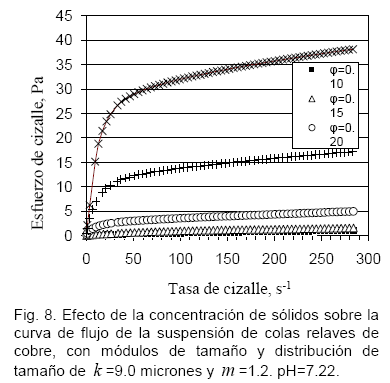
Los resultados de las mediciones reológicas de estas suspensiones están presentados en las curvas de flujo de la Fig. 8.
Las pulpas de estas concentraciones tienen fuerte comportamiento de fluidos no-Newtonianos, aun a la concentración de ![]() =0.10, todas exhiben esfuerzo de cedencia. Asimismo, el fenómeno de desliz del mencionado equipo con cada una de las suspensiones medidas en el rango de tasa de cizalle de
=0.10, todas exhiben esfuerzo de cedencia. Asimismo, el fenómeno de desliz del mencionado equipo con cada una de las suspensiones medidas en el rango de tasa de cizalle de ![]() es muy marcado.
es muy marcado.
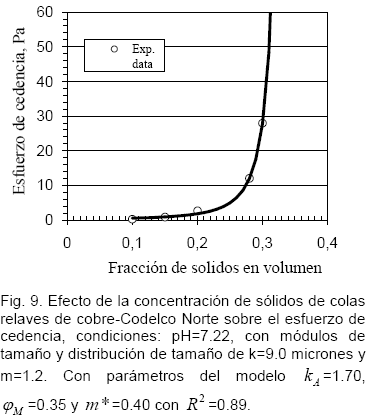
De los resultados de la Fig. 9, se muestra que el modelo propuesto es capaz de predecir el esfuerzo de cedencia de las suspensiones con propiedades distintas al estudiado con suspensiones de cuarzo.
La fuerte influencia de la concentración de sólidos sobre el esfuerzo de cedencia en la descarga del espesador de colas relaves de Codelco Norte, esto implica que, con pequeños incrementos en la concentración sólidos, puede traer serios problemas de orden mecánico, esto es, el torque sobre las rastras utilizadas en el movimiento del material espesado de los espesadores. El parámetro crítico en la descarga del espesador es la máxima fracción de empaquetamiento![]() relacionado al esfuerzo de cedencia
relacionado al esfuerzo de cedencia![]() . El contenido de sólidos cercano al
. El contenido de sólidos cercano al![]() (
(![]() =0.35) genera valores de
=0.35) genera valores de![]() muy altos. Por tanto, la fuerza necesaria para vencer el
muy altos. Por tanto, la fuerza necesaria para vencer el![]() tendrá valores muy altos. De donde, se puede deducir, la concentración de pulpa de la descarga del espesador debe tener valores muy por debajo de la fracción de empaquetamiento de
tendrá valores muy altos. De donde, se puede deducir, la concentración de pulpa de la descarga del espesador debe tener valores muy por debajo de la fracción de empaquetamiento de![]() =0.35.
=0.35.
El esfuerzo de cedencia es fuertemente dependiente, además de la concentración de sólidos y tamaño de partículas, como de la naturaleza de la suspensión como es el caso de los relaves del mineral de cobre con polímeros usados como floculantes.
Los altos niveles de esfuerzo de cedencia encontrados con suspensiones de relaves de cobre implicaría dos situaciones, 1) que la pulpa pueda ser bombeada en flujo laminar a grandes distancias sin riesgo de problemas de deposición de sólidos y también menos problemas asociados con el reinicio una vez haya parado la operación, 2) un alto valor de esfuerzo de cedencia requiere de altas presiones de bombeo, por tanto, esta asociado a altos costos de operación en sistemas de tuberías (Nguyen y Boger, 1998; Kwaket al. 2005).
5.-Conclusiones
El modelo de esfuerzo de cedencia basado en el análisis conceptual del espacio disponible que una partícula pueda moverse en un espacio limitado por![]() (grados de libertad de la partícula), para suspensiones con comportamientos de fluidos no Newtonianos, fue validado con datos experimentales de suspensiones de cuarzo con un amplio rango de concentraciones de sólidos (
(grados de libertad de la partícula), para suspensiones con comportamientos de fluidos no Newtonianos, fue validado con datos experimentales de suspensiones de cuarzo con un amplio rango de concentraciones de sólidos ( ![]() =0.25-0.51).
=0.25-0.51).
Asimismo, el tamaño involucrado en el modelo predice con éxito el efecto de un amplio rango de tamaños de partículas de la suspensión de cuarzo (k =11, 15, 22, 36 y 46 micrones) sobre el esfuerzo de cedencia.
Las partículas finas reportan valores de empaquetamiento de baja densidad en relación a tamaños de partículas gruesas. Para suspensionescercanas al empaquetamiento máximo (![]() ), el esfuerzo de cedencia adquiere valores muy altos. El modelo fue aplicado a suspensiones de relaves de cobre de Codelco Norte de la gran minería chilena. Los resultados muestran una buena descripción del modelo con sistemas reales.
), el esfuerzo de cedencia adquiere valores muy altos. El modelo fue aplicado a suspensiones de relaves de cobre de Codelco Norte de la gran minería chilena. Los resultados muestran una buena descripción del modelo con sistemas reales.
Agradecimientos
Se agradecen al Programa de Doctorado en Ingeniería Metalúrgica del Departamento de Ingeniería Metalúrgica de la Universidad de Concepción-Chile por la beca concedida para realizar estudios de Postgrado y al señor Patricio Leonelli del Laboratorio de Reología por las mediciones de análisis granulométrico de las muestras de cuarzo y relaves de cobre.
Referencias
Addai-Mensah, J., Ralston, J., 2004. Interfacial chemistry and particle interactions and their impact upon the dewatering behavior of iron oxide dispersions. Hydrometallurgy 74. 221-231. [ Links ]
Akroyd, T. J., 2004. Continuous Flow Rheometry for settling Slurries, Thesis of Doctorate, University of Adelaide. [ Links ]
Barnes, H. A., Hutton, J. F., Walters, K., 1989. An introduction to Rheology, Rheology Series 3. Elsevier, Amsterdam. [ Links ]
Chang, C., Powell, R.L., 2002. Hydrodynamic Transport Properties of Concentrated Suspensions. AIChE Journal 48, 11, 2475-2480. [ Links ]
Concha, F., Barrientos, A., 1993. Mecánica Racional Moderna, Vol. II Termodinámica del Medio Continuo, Serie en Mecánica Racional Moderna, Departamento de Ingeniería Metalúrgica, Universidad de Concepción. [ Links ]
Dabak, T., Yucel, O., 1987. Modeling of the Concentration and Particle Size Distribution Effects on the Rheology of Highly Concentrated Suspensions. Powder Technology 52, 193-206. [ Links ]
Ding, Z., Yin, Z., Liu, L., Chen, Q., 2007. Effect of grinding parameters on the rheology of pyrite-heptane slurry in a laboratory stirred media mill. Minerals Engineering 20, 701-709. [ Links ]
Einstein, A., 1956. Introductions on the theory of the Brownian muvement, Dover publications Inc. N.Y. [ Links ]
Fuerstenau, D. W., Jia, R., 2004. The adsorption of alkylpyridinium chlorides and their effect on the interfacial behavior of quartz. Colloids and Surfaces A: Physicochem. Eng. Aspects 250, 223-231. [ Links ]
Fornasiero, D., Ralston, J., 2005. Cu(II) and Ni(II) activation in the flotation of quartz, lizardite and chlorite. Int. J. Miner. Process. 76, 75-81. [ Links ]
Flatt, R. J., 2006. Yodel: A Yield Stress Model for Suspensions. J. Am. Ceram. Soc. 89, 4 1244-1256. Guo, J., Tiu, C., Uhlherr, P. H., Fang, T. N., 2003. Yielding behavior of organically treated anatase TiO2 suspension. Korea-Australia Rheology Journal 15, 1, 9-17. [ Links ]
Gustafsson, J., Nordenswan, E., Rosenholm, J. B., 2003. Effect of pH on the sedimentation, z-potential, and rheology of anatase suspensions. Colloids and Surfaces A: Physicochem. Eng. Aspects 212, 235-247. [ Links ]
Harbour, P. J., Dixon, D. R., Scales, P. J., 2007. The role of natural organic matter in suspension stability 2. Modelling of particle-particle interaction. Colloids and Surfaces A: Physicochem. Eng. Aspects 295, 67- 74. [ Links ]
Hauptkorna, S., Krivan, V., Gercken, B., Pavel, J., 1997. Determination of Trace Impurities in High-purity Quartz by Electrothermal Vaporization Inductively Coupled Plasma Mass Spectrometry Using the Slurry Sampling Technique. Journal of Analytical Atomic Spectrometry 12, 421- 428. [ Links ]
He, M., Wang, Y., Forssberg, E., 2004. Slurry rheology in wet ultra fine grinding of industrial minerals: A review, Powder Technology 147. [ Links ]
He, M., Wang, Y., Forssberg, E., 2006a. Parameter studies on the rheology of limestone slurries. Int. J. Miner. Process. 78, 63-77. [ Links ]
Huynh, L., Jenkins, P., Ralston, J., 2000. Modification of the rheological properties of concentrated slurries by control of mineral-solution interfacial chemistry. Int. J. Miner. Process. 59, 305-325. [ Links ]