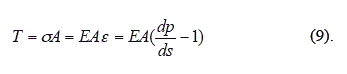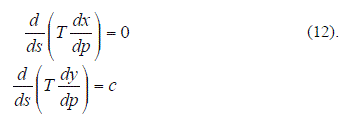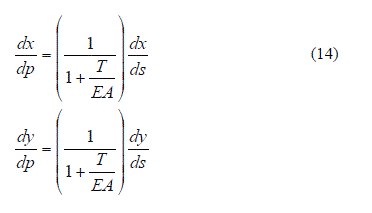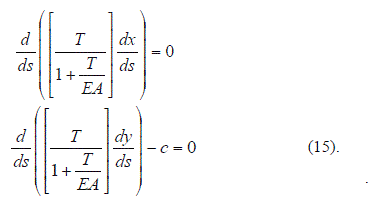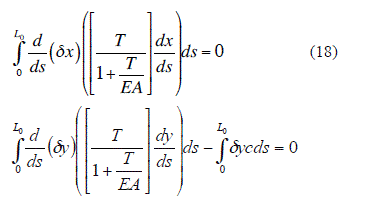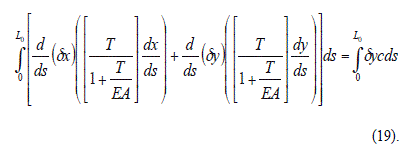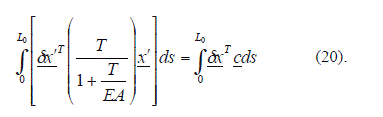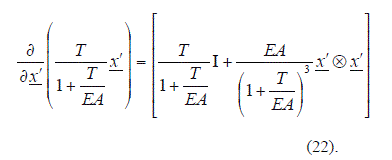INVESTIGACIÓN CIENTÍFICA

 

Análisis estático geométricamente no-lineal de estructuras
de cable,considerando linealidad física

 

 

MsC. Ing. Eduardo Gianella Peredo
Docente Investigador Facultad de Ingeniería en
Ciencias de la Computación y Telecomunicaciones
UAGRM.

 

 

---

Resumen

En este trabajo se establece la formulación variacional del problema estático de cable, considerando no-linealidad geométrica y linealidad física. Esta formulación es requerida para el análisis por elementos finitos del problema.

Es utilizado un enfoque basado en coordenadas absolutas y una descripción Lagrangiana.

Palabras clave: Cable, Elemento Finito, Análisis No-Lineal.

---

 

 

INTRODUCCIÓN

La idea de construir estructuras ligeras para salvar grandes luces se origina en tiempos remotos, cuando el ingenio del hombre fue puesto a prueba a través de los caprichos de la naturaleza, que le imponía el problema de salvar obstáculos en su trayecto, como cañones o ríos caudalosos. La estructura que resolvió esta situación fue el puente colgante, en el cual los elementos resistentes fundamentales eran cables elaborados con material vegetal. Otra aplicación de cables en la antigüedad, muy sofisticada para la época, lo constituye la cubierta colgante del coliseo de Roma, construido durante el siglo primero.

La gran importancia que nuestros antepasados le dieron al desarrollo de modelos matemáticos para el estudio de los cables, ha quedado registrada por el trabajo incansable de muchos científicos a través de de nuestra historia.

Según J. Bukowski, Chistiaan Huygens, en 1638 Galileo concluye erróneamente que la forma de una cadena, sostenida por sus extremos y resistiendo apenas su propio peso, corresponde a una parábola.

La verdadera ecuación de la cadena colgante, sin considerar su deformación, es descubierta en 1691, en forma independiente, por los científicos Johann Bernoulli, Gottfried Leibniz y Christiaan Huygens. Esta curva fue nombrada por Huygens con el término "catenaria" que deriva del latín "catena" que significa cadena.

Al considerar al cable como extensible, se añade un grado adicional importante de complejidad, que obliga a resolver las ecuaciones resultantes, no lineales, por medio de métodos numéricos. En la década de los cuarenta del siglo pasado, sin las computadoras, los métodos numéricos no eran una opción práctica para el análisis de los cables, y por este motivo, los investigadores de la época desarrollaron apenas soluciones analíticas cerradas para situaciones muy simplificadas.

Con el advenimiento de las computadoras y la introducción del Método de los Elementos Finitos, a mediados del siglo pasado, se inicia una fructífera etapa de producción científica sobre el tema de estructuras de cable.

Desde el punto de vista del análisis estructural, las estructuras de cable presentan una gran dificultad, que consiste en el desconocimiento de su configuración inicial. El origen de este problema radica en que los cables trabajan estructuralmente y únicamente a tracción, lo cual conlleva una fuerte dosis de no-linealidad geométrica, originando inestabilidad numérica en los algoritmos de solución.

En la actualidad, con los logros conseguidos en la ingeniería de materiales y el grado de desarrollo alcanzado por la informática, aparecen cables de alta resistencia y modelos matemáticos muy sofisticados para el análisis de los mismos.

Los cables son incluidos, cada vez con mayor frecuencia, como elementos resistentes a tracción en obras de ingeniería de gran envergadura, como ser puentes colgantes, puentes atirantados, cubiertas colgantes, líneas de tendido eléctrico, líneas de anclaje de estructuras marinas y muchas otras.

A continuación se detalla y comenta una lista de importantes trabajos sobre el asunto:

J. J. Russell y W. J. Anderson, usan un elemento finito de deformación constante para el estudio dinámico de cables.

W. M. Henghold y J. J. Russell, Desarrollan una clase de elementos finitos de cable que permiten el análisis geométricamente no-lineal y grandes pero elásticas deformaciones.

A. H. Peyrot, y A. M. Goulois, construyen un elemento finito tipo catenaria, para el análisis estático de cables, sin embargo no completan su matriz de rigidez para un análisis tridimensional.

H.B.Jayaraman, W.C. Knudson, modifican el elemento presentado mediante la inclusión de su rigidez en dirección normal al plano del cable y consiguen utilizarlo en análisis tridimensional.

H. Ozdemir, aborda el problema estático y dinámico de cables usando elementos finitos e imponiendo únicamente continuidad de desplazamientos en los nodos.

E. Oshima de Aguiar, desarrolla un elemento finito rectilíneo isoparamétrico, para analizar el problema estático de cables considerando no-linealidades física y geométrica.

I.Talvik presenta un modelo matemático para el análisis de estructuras de cable con vigas de contorno flexible.

M. Salehi Ahmad Aba, A. Shooshtari, V. Esmaeili, A. Naghavi Riabi, desarrolla dos elementos finitos de cable, el primero llamado Continuo Cable Catenaria (CCC), que es una extensión del clásico elemento catenaria, y el segundo Discreto Cable Catenaria (DCC) que utiliza las ecuaciones del (CCC) discretizadas.

L.Greco, N.lmpollonia, M.Cuomo, utiliza un elemento finito de tipo catenaria tridimensional, que admite fuerzas distribuidas y concentradas en el interior del elemento.

 

ECUACIONES QUE GOBIERNAN EL PROBLEMA ELÁSTICO-ESTÁTICO DEL CABLE DEFORMABLE.

En la siguiente figura "c" representa la fuerza por unidad de longitud del cable.

Se escriben a continuación las ecuaciones para el cable, usando como referencia la figura 1 y el desarrollo establecido por Wei. R, Bingnan S., Jinchun, T.

Para el cable elástico, L y L_o representan su longitud deformada en la configuración actual y su longitud sin ninguna deformación en la configuración de referencia, respectivamente.

Equilibrio global impone las siguientes relaciones entre las fuerzas nodales:

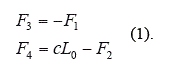
Equilibrio en nodos de extremo del cable:

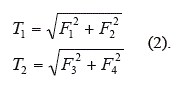
Restricción geométrica:

Considerando el equilibrio del tramo del cable, mostrado en la figura 2, se obtiene:

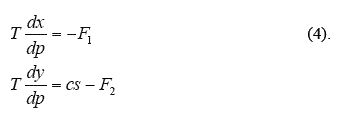
Dividiendo ambas por T pueden escribirse como:

Elevando al cuadrado ambos miembros de cada una de estas ecuaciones, sumando término a término y llevando en cuenta (3), se llega a:

La deformación específica lineal experimentada por la longitud del cable ds, mostrada en la figura 2, es dada por:

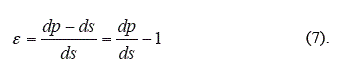
La correspondiente tensión normal es:

En (8)" E" es el módulo de Young del material.

La tensión en la posición definida por "p" es:

Finalmente a partir de (9) se obtiene:

 

FORMULACIÓN VARIACIONAL

Para aplicar el método de los elementos finitos, es necesario construir la "formulación variacional" del modelo matemático del cable, también llamada "formulación débil". Existen distintos caminos para obtener la formulación variacional. En este trabajo se utiliza "El Método de los Residuos Ponderados.

 

MÉTODO DE LOS RESIDUOS PONDERADOS

Este procedimiento parte de las ecuaciones de equilibrio y sus condiciones de contorno, también llamadas "formulación fuerte" del problema.

Condiciones de contorno:

Como indicado en [4], derivando las expresiones (11) respecto a "s" se llega a:

Utilizando la regla de la cadena:

Introduciendo en (10) en las expresiones (13) se obtiene:

Considerando (14) las expresiones (12) pueden escribirse como:

Las ecuaciones (15) constituyen las derivadas respecto a "s" de los "residuos" que resultan en las ecuaciones de equilibrio cuando se introducen en ellas aproximaciones x(s) y y(s).

Se definen δx(s) y δy(s) como funciones de ponderación, las cuales deben ser derivables en su dominio y también deben anularse en el contorno.

Se imponen a continuación las condiciones que originan el nombre del método:

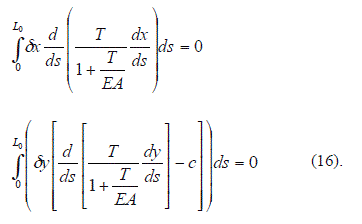
Integrando por partes las ecuaciones (16) resulta

Recordando que δx(s) y δy(s) se anulan en el contorno, las condiciones (17) se reducen a:

Sumando término a término las igualdades (18) se llega a:

Definiendo las matrices

(19) puede escribirse como:

(20) constituye la formulación variacional del problema y representa la imposición del equilibrio en el cable. Sin embargo T depende de , modo que esta ecuación resulta ser no-lineal en .

Debido al carácter no-lineal de (20) y asumiendo una resolución numérica de la misma por el método iterativo de Newton-Raphson, es necesario expresarla en forma incremental.

Considerando el incremento de la carga, las coordenadas de los puntos del cable deben incrementarse también en para que las fuerzas internas retomen el equilibrio. Esta relación entre incrementos adopta la siguiente forma matemática:

Para determinar el gradiente de

Se utiliza la siguiente identidad del cálculo tensorial:

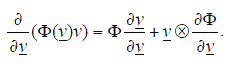
Luego de aplicar la identidad indicada y simplificar la expresión algebraica resultante, se obtiene:

Donde I es la matriz identidad 2x2.

Introduciendo (22) en (21), se llega a la relación incremental entre fuerzas internas y externas.

 

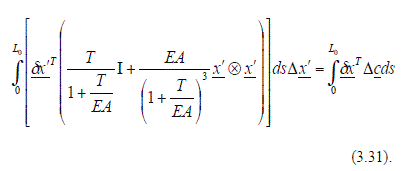
CONCLUSIONES Y RECOMENDACIONES

Se ha logrado en este reporte deducir la formulación variacional del problema de cable y su forma incremental, las cuales constituyen el punto de partida para la aplicación del método de los Elementos Finitos. Trabajos adicionales son requeridos para implementar diferentes elementos y elaborar un programa de computador que pueda simular el modelo matemático desarrollado.

 

BIBLIOGRAFÍA

Irvine, H.M., 1982. Cable Structures. Dover Publications, New York.        [ Links ]

Wang, Z., McCarthy, I, Sheikh, M. Neaz 2011. Taut-Slack algorithm for analyzing the geometric nonlinearity of cable structures. 21^st. International Offshore and Polar Engineering Conference, ISOPE-201, pp. 188-194, United States: International Society of Offshore and Polar Engineers.        [ Links ]

Wei, P, Bingnan, S., Jinchun,T. 1999. Acatenary element for the analysis of cable structures. Applied Mathematics and Mechanics, vol. 20, No. 5, pp 532-534.        [ Links ]

Hae Sung Lee 2006. A Stabilization Technique for the Dynamic Analysis of Slack Cables. MSc Thesis, Seoul National University Earth and Environmental Systems Engineering Park Young Iron.        [ Links ]

Aguiar, Elisabeth Oshima 1999. Contribuicá ao Estudo de Estruturas de Cabos para Coberturas de Grandes Areas Livres, Considerando as Nao Linearidades Física e Geométrica. Tese de Doutorado, Escola de Engenharia de Sao Carlos EESC.        [ Links ]

J. J. Russell, W. J. Anderson 1975. Whirling cable subjected to viscous drag. Proc. of the Int. Conf. on Finite Elements in Engng. pp 661- 675. University of New South Wales.        [ Links ]

W. M. Henghold, J. J. Russell 1976. Equilibrium and natural frequencies of cable structures (un nonlinear finite element approach). Computers & Structures, Vol. 6 pp. 267-271 Pergamon Press.        [ Links ]

A. H. Peyrot, and A. M. Goulois 1979. Analysis de cable structures. Computers & Structures, Vol. 16 pp. 885-913 Pergamon Press.        [ Links ]

H. Ozdemir 1979. A finite element approach for cable problems. Int. J. Solids Structures. Vol. 15 pp. 427-437. Pergamon Press.        [ Links ]

I.Talvik 2001. Finite element modelling of cable networks with flexible supports. Computers & Structures, Vol. 79 pp. 2443-2450. Pergamon Press.        [ Links ]

M.Salehi Ahmad Aba, A.Shooshtari,V Esmaeili, A. Naghavi Riabi 2013. Nonlinear analysis of cable structures under general loadings. Finite Element in Analysis and Design Vol. 73 pp. 11-19.        [ Links ]

L.Greco, N.lmpollonia, M.Cuomo 2014. A Procedure for the static Analysis of Cable Structures Following Elastic Catenary Theory. International Journal of Solids and Structures Vol. 51 pp. 1521-1533.        [ Links ]

H. B. Jadyaraman, W.C. Knudson 1981. A curved element for the analysis of cable structures. Computers & Structures, Vol. 14 pp. 325-333 Pergamon Press.        [ Links ]

J. Bukowski. Christiaan Huygens and the Problem of the Hanging Chain, v. 39, no. 1, January 2008 The College Mathematics Journal.