INVESTIGACIÓN

 

APLICACIONES DE LA PROGRAMACIÓN LINEAL (PL) EN INVESTIGACIÓN DE OPERACIONES -ALGORITMO SIMPLEX (AS) (Cuatro ejemplos relacionados con la optimización de funciones y la asignación de variables implicadas)

 

APPLICATIONS OF LINEAR PROGRAMMING (LP) IN OPERATIONS RESEARCH - SIMPLEX ALGORITHM (SA) (Four examples related to optimization of functions and assignment of variables involved)

 

 

Erick C. Grudner Carranza*
(*), Químico Industrial, Consultor Productividad, Calidad e Innovación Tecnológica, Diplomado Investigación Operativa, Editor Revista Tecnológica, Facultad de Tecnología - UMSA.
History of the article: Received 07/10/2021. Style review 14/10/2021. Accepted 28/10/2021.

 

 

---

RESUMEN

Este artículo de divulgación de la programación lineal (PL); busca recrear los alcances e importancia del algoritmo simplex (AS) en la investigación de operaciones y la toma de decisiones estratégicas. Presentando primero los fundamentos matemáticos del (AS), y a continuación aplicándolos, en cuatro ejemplos relacionados con la optimización de funciones objetivo y asignación de las variables implicadas, resaltando su objeto común de estudio, los criterios para su desarrollo e inclusión de variables auxiliares según los signos que definen las inecuaciones (restricciones) de programas lineales: primales, duales, paramétricos y enteros.

PALABRAS CLAVE: Optimización lineal, programación lineal, algoritmo Dantzig-Kantoróvich (simplex), función objetivo, asignación óptima de variables, investigación de operaciones, maximización, minimización.

---

ABSTRACT

This linear programming (LP) popularization article; seeks to recreate the scope and importance of the simplex algorithm (SA) in operations research and strategic decision making. Presenting first, the mathematical foundations of the (SA), and then applying them, in four examples related to the optimization of objective functions and assignment of the variables involved, highlighting their common object of study, the criteria for their development and inclusion of variables auxiliaries according to the signs that define the inequalities (restrictions) of linear programs: primal, dual, parametric and interger.

KEYWORDS: Lineal optimization, linear programming, Dantzig-Kantoróvich algorithm (simplex), objective function, optimal assignment of variables, operations research, maximization, minimization.

---

RESUMO

Este artigo de popularização de programação linear (LP); busca recriar o escopo e a importância do algoritmo simplex (AS) na pesquisa operacional e na tomada de decisões estratégicas. Apresentando primeiro, os fundamentos matemáticos do (AS), e depois aplicando-os, em quatro exemplos relacionados á otimização de funções objetivo e atribuição das variáveis envolvidas, destacando seu objeto comum de estudo, os critérios para seu desenvolvimento e inclusão de variáveis auxiliares de acordo com os sinais que definem as desigualdades (restrições) de programas lineares: primal, dual, paramétrico e inteiro.

PALABRAS-CHAVE: Otimização linear, programação linear, Algoritmo Dantzig-Kantoróvich (simplex), função objetivo, designação ótima de variáveis, investigação de operações, maximização, minimização.

---

 

 

INTRODUCCIÓN

Optimización[1], marco conceptual

De modo explícito o implícito la optimización como parte de las actividades humanas, sean éstas personales o laborales, busca encontrar ese algo que no puede ser mejor. Esto significa encontrar lo óptimo (superlativo de bueno) desde el punto de vista del objetivo planteado.

En consecuencia, frente a la variedad real de problemas referidos especialmente con la distribución de recursos limitados de los factores de producción (trabajo, capital, materias primas), el análisis de productividad de los procesos de producción, la toma de decisiones sobre aspectos cuantitativos y cualitativos de la administración empresarial (investigación de operaciones), y el diseño de objetos complejos [1]. La optimización o programación matemática como un campo de estudio de la matemática pura y aplicada, proporciona los métodos generales para solucionar estos problemas, estableciendo inicialmente el enunciado del problema que interesa resolver en términos matemáticos considerando estimaciones cuantitativas a las posibles variantes, evaluadas desde la perspectiva discriminante de un valor mínimo o máximo de la función objetivo[2].

Por lo tanto, el planteamiento del problema y los métodos de investigación para lograr la optimización dependen tanto de las propiedades de la función objetivo como de la información disponible al respecto. Simplificándose la solución del problema, cuando la función objetivo se expresa mediante una fórmula o un polinomio de grado mayor a uno y es derivable, condición que permite analizar las propiedades de la función, determinar la

dirección de su crecimiento o decrecimiento y buscar los puntos extremos (máximos y mínimos) [1]. Separándose de este método general de optimización, la programación lineal (LP), que a través de algoritmos especiales soluciona funciones objetivo multivariable de grado uno.

Programación lineal (PL)

Expresa en términos matemáticos un problema real y sobre éste, modela un procedimiento analítico para encontrar ya sea el valor máximo[3] o el mínimo[4]de una cantidad específica denominada función objetivo, la cual depende de un número finito de variables de entrada independientes entre sí, o relacionadas a través de una o más restricciones que se expresan por medio de una serie de inecuaciones[5]y ecuaciones lineales (grado uno) que resueltas proporcionan una solución posible dentro de ese espacio restringido de valores que acompañan a estas variables [3]. La función objetivo puede maximizarse o minimizarse resolviendo analíticamente simples sistemas algebraicos de inecuaciones y ecuaciones lineales o por su representación gráfica. Para los casos donde se presentan un mayor número de variables y restricciones, se utiliza el algoritmo de Dantzig denominado método del algoritmo simplex (SA). Procedimiento algorítmico de balanceo (pivote) muy recurrente para abordar problemas de investigación operativa[6]en general.

Consecuentemente en este artículo de divulgación de la programación lineal (PL); se busca recrear los alcances e importancia del algoritmo simplex (SA) en la investigación de operaciones y la toma de decisiones estratégicas. Presentando brevemente los fundamentos matemáticos del algoritmo simplex (SA), y a continuación aplicándolos, en cuatro ejemplos relacionados con la optimización de funciones objetivo y asignación de las variables implicadas, resaltando su objeto común de estudio, los criterios para su desarrollo e inclusión de variables auxiliares según los signos que definen las inecuaciones (restricciones) de programas lineales: primales, duales, paramétricos y enteros.

 

DESARROLLO

Algoritmo de Dantzig[7], (algoritmo simplex SA)

Procedimiento matricial iterativo de programación lineal; suficiente para dar solución a problemas con un mayor número de variables y de restricciones representadas por un sistema de inecuaciones o desigualdades que definen a un poliedro como el espacio geométrico factible por donde avanzando sucesivamente desde uno de sus vértices[8], se puede llegar a otro de los vértices, dónde está la solución óptima que maximiza o minimiza la función objetivo [3].

Representación estándar del algoritmo simplex (SA)

En su forma matricial estándar (SA) reúne la función objetivo ha optimizar, las restricciones y la condición que todas las variables sean positivas (mayores a cero):

El método simplex para los programas de optimización recurre a la construcción de una tabla especial (tableau), figura 1. En la cual (C₀) corresponde al vector costo, asociado con las variables en (X₀).

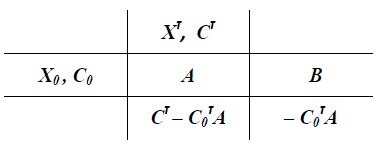
Fuente: Elaboración propia sobre información de [3], [4]
Figura 1: Tabla especial (tableaux)

Construcción de tablas e iteración simplex

Sea el siguiente problema de programación lineal (LP) donde se quiere maximizar la función objetivo z (Ec.1):

Fuente: Elaboración propia sobre datos problema propuesto en [5]

Examinando el programa lineal de maximización, la función objetivo involucra a tres variables {x_h x₂, x₃) y las restricciones incluyen dos desigualdades de la forma (<) menor o igual que, para convertirlas en ecuaciones, requieren incorporar dos slacks variables (variables de holgura (s₄, s₅) de coeficientes cero para la función objetivo y uno respectivamente para la matriz (A).

x₁ + 6x₂ + x₃ + 0s₄+ 0s₅-z = 0          ( Ec. 4)

x₁+ 2x₂ + 3x₃ + s₄ = 9                           (Ec. 5)

3x₁ + 2x₂ + 2x₃ + s₅ = 15                       (Ec. 6)

Relacionando la tableaux (figura 1) con los coeficientes de estas ecuaciones, se tiene el detalle siguiente:

Efectuando el producto interno para las matrices:

Fuente: Elaboración propia sobre datos problema propuesto en [5]

En la tableaux 1, se muestra el traslado de estos datos en un formato de tabla común, considerando también el cambio de signo fila (z_j) para la opción maximizar. A partir de esta tableaux es posible aplicar el algoritmo simplex, identificando inicialmente la columna (C_b) y luego la fila de balanceo (Rf) (column and row pivot):

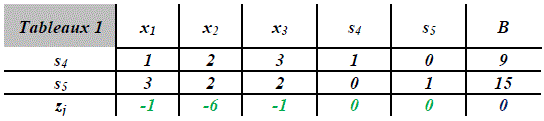
Para la columna de balanceo (C_b), se examina aquella con el valor negativo zj más extremo; y para la fila de balanceo (R_f) se elige el cociente (B/casilla C_b) menor, tableaux 2:

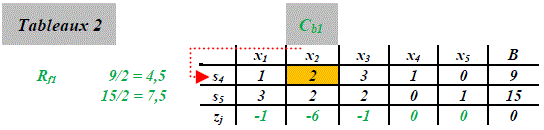
Elegida la fila de balanceo (R_f) se cambia la variable de la columna de balanceo por la variable de la fila marcada por el cociente menor, las casillas de la columna de balanceo se convierten en uno (fila de balanceo) y ceros para las otras filas [4], [5]. Las operaciones correspondientes para este caso se muestran en la tableaux 3:

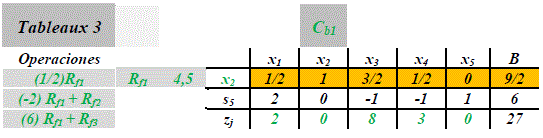
Operaciones sobre la tabla 1:

De esta forma el algoritmo continua iterando valores hasta llegar a la condición de parada (stop condición, cambio de signos en la fila z_j) [4]. Al respecto en la tableaux 3 se observa que la fila (z_j) ya no tiene valores con signo negativo. En consecuencia, el algoritmo ha llegado a la condición de parada, determinando los siguientes valores para la maximización de esta función objetivo:

Z = 6x₂ = 27, variables x₁ =x₃ = 0, x₂= (9/2) =4,5 y s₅ = 6

Remplazando el valor de x₂ y el valor de s₅ en la ecuación 6, se tiene que:

2(4,5)+ 6 = 15

La variable slack o de holgura indica que la inecuación 3 incorpora un excedente de seis.

Asistencia computacional para aplicar el algoritmo simplex (SA)

El algoritmo simplex a partir de sus primeras aplicaciones en la década de los cuarenta (siglo XX) ha requerido de sistemas de cálculo que agilicen los tiempos de iteración hasta llegar a los resultados. Más aún, sí en los problemas de programación lineal el número de variables y restricciones es demasiado grande. Al respecto la computación ha extendido grandemente sus posibilidades tanto en software como en hardware para ofrecer a los usuarios aplicaciones que resuelven simples y complejos programas lineales de optimización.

Al presente estas aplicaciones también son parte de los catálogos de calculadoras manuales[9]. Igualmente a través de Internet[10], es posible acceder a páginas web que ofrecen la resolución en tiempo real de programas lineales de maximización o minimización, entregando los resultados y adicionalmente un auxiliar de los cálculos efectuados.

Para el caso del programa lineal presentado en los parágrafos anteriores como modelo. Visitando las páginas [6] www.simplexme.com y [7] www.phpsimplex.com, en ambas, el primer paso corresponde a determinar el número de variables y restricciones; ingresados estos datos, el programa abre una matriz para incluir los coeficientes tanto para la función objetivo, y los coeficientes de las restricciones, además de las opciones del programa (maximizar o minimizar). Continuando aparece de inmediato la solución y al mismo tiempo cierta información adicional, ver screenshot editado (figura 2).

Fuente: [6]
Figura 2: Solución (LP) modelo, pasos seguidos (2), cambio de variables de columna a fila, según aplicación simplexme.

De similar forma en la aplicación PHPsimplex, ingresando los datos y continuando el proceso algorítmico simplex, la conclusión se muestra en el screenshot editado de la figura 3. Si bien en ambas aplicaciones el diseño de la tabla inicial difiere significativamente, los resultados convergen hacia la única solución posible de este programa lineal de maximización, coincidente con los resultados obtenidos al desarrollar el algoritmo simplex para el modelo (Ec. 1 e Inecs. 2 y 3).

Fuente: [7]
Figura 3: Solución (LP) modelo, cambio de variables de columna, opción vista de cálculos efectuados, y finalmente el resultado según aplicación phpsimplex.com.

Inclusión de variables según el signo de la inecuación

El algoritmo simplex de acuerdo con el signo que tienen las inecuaciones propuestas en el programa lineal, necesita determinadas variables artificiales según el signo de las restricción [4], así el tipo de variable a incluir corresponde a

Primer ejemplo:

Restricciones con signo menor o igual (≤). Asignación óptima de recursos en procesos de producción:

En una empresa de la ciudad de la Paz dedicada a la comercialización de café torrado en bolsas de uno, medio y cuarto kilo; se buscó maximizar el costo del proceso de envasado en relación con el número de bolsas según el peso de café, considerándose las siguientes variables:

1. Cantidad diaria total de café torrado a envasar,

2. Tiempo mínimo de llenado según el peso,

3.  Pérdidas en el llenado de las bolsas según el peso (Ineficiencia de llenado),

4. Total bolsas producidas por día.

Esta información se representa con el siguiente programa lineal de aplicación algoritmo simplex PLAS:

Fuente: Elaboración propia

Cambio desigualdades a ecuaciones incluyendo variables de holgura:

Soluciones

Para optimizar este programa por el método algebraico de solución de ecuaciones lineales se condicionarían de acuerdo con el cálculo combinatorio 35 posibles soluciones que resultan de aplicar la fórmula combinatoria:

De estas 35 iteraciones. El óptimo pertenece al siguiente desarrollo matricial, seleccionado variables (x₁, x₂, x₃, s₇):

Fuente: Desarrollo matricial propio, captura de pantalla hoja Excel

Solución aplicando algoritmo simplex

Tabla simplex de inicio, efectuando por convención el cambio de signo para los coeficientes de las variables función objetivo, además otorgando la unidad para cada variable de holgura (s) en la matriz A[11].

Fuente: Elaboración propia, edición captura de pantalla hoja Excel

Primera columna de balanceo, se elige la que contiene el valor negativo más extremo (z), columna x3. Para la fila de balanceo según el criterio discriminante menor cociente (Sol./Casilla columna de balanceo 750, 1125. 2583,3 y 1800), determina que es la fila 2. Por lo tanto la tabla 1 puede representarse de la siguiente manera. En el extremo izquierdo de la tabla se incluyen las operaciones que permiten convertir la casilla de intersección (fila-columna) a la unidad y las otras casillas de la misma columna a cero). Para la tabla 1 la intersección es igual a la unidad; por lo tanto, no requiere.

La iteración del algoritmo, efectuando las operaciones correspondientes proporciona la tabla 2. Seleccionando la columna x₁ como la del valor negativo más extremo y la fila de balanceo f₄, correspondiendo la intersección a 0,0425. Cifra que ahora sirve para su conversión a la unidad, desarrollando el producto por su recíproco (1/0,0425). Afectando además a toda la fila y cambio en las operaciones.

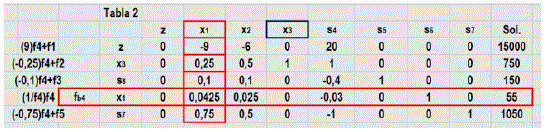
Fuente: Elaboración propia, edición captura de pantalla hoja Excel

La ejemplificación permite calcular la nueva fila f₁ tabla 3.

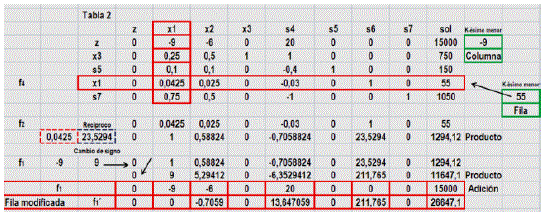
Fuente: Elaboración propia, edición captura de pantalla hoja Excel

Prosiguiendo con las operaciones para las demás filas y columnas el resultado se muestra en la tabla 3.

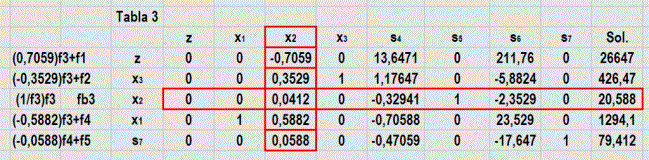
Existiendo todavía un valor negativo extremo, la iteración prosigue efectuando las operaciones correspondientes y el cambio en la columna x₂, para finalmente determinar la condición de parada (tabla 4[12]) que además incluye la solución al programa lineal propuesto en el ejemplo uno.

Fuente: Elaboración propia, edición captura de pantalla hoja Excel

Solución utilizando la aplicación PHPsimplex

La siguiente captura de pantalla, corresponde al resultado obtenido recurriendo a la aplicación PHPsimplex, que es igual al conseguido a través de la aplicación explicativa Excel y del método algebraico. Diferenciándose notablemente por el tiempo transcurrido para la entrega del resultado.

Fuente: [7]

Análisis de los resultados problema uno

Asignadas las variables para este proceso productivo proporciona la siguiente información:

•       Capacidad de envasado limitante 750 Kg, distribuida así; 1000 bolsas de 0,25 Kg, 500 bolsas de 0,5 Kg y 250 bolsas de 1 Kg.

•       Estableciendo además que el tiempo de llenado y la pérdida de producto por peso, también son variables limitantes que pueden servir para controlar el proceso diariamente.

•      Total diario de bolsas producidas de acuerdo con 750 Kg de café torrado y las restricciones (tiempo de embolsado y perdidas), Que corresponde al total real de 1750 a diferencia del valor estimado de 1800, (slack variable, s₇ = 50).

•       Mezcla productiva de café (0,25 - 0,5 - 1)Kg maximizada con un valor de 27000 unidades monetarias.

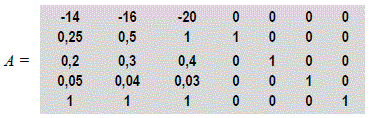
Información útil para la toma de decisiones que mantenga estas variables o pueda utilizarlas para replantear la función objetivo y/o sus restricciones. Bajo este enfoque de programación paramétrica y análisis de sensibilidad [8], [9]. [10], [11], [12] Efectuando modificaciones para el proceso de envasado relacionadas con un aumento en la cantidad de café a envasar diariamente del 33,33 porciento y reduciendo las pérdidas hasta un 32 porciento. Manteniendo invariable los coeficientes de la función objetivo (costos de producción). La nueva programación lineal establece lo siguiente:

0,25x₁ + 0,5x₂ +x₃+s₄= 1000 (Ec. 12)

0,2x₁ + 0,2x₂ + 0,3x₃ +s₅ = 450 (Ec. 13)

0,03x₁ + 0,025x₂ + 0,02x₃ + s₆=53 (Ec. 14)

x₁+x₂+x₃ +s₇ =2000 (Ec.10)

z = 14x₁ + 16x₂ + 20x₃ + 0s₄ + 0s₅ + 0s₆ + 0s₇ (Ec. 15)

Desarrollando el algoritmo simplex hoja Excel (ver tablas 5 a 8), y la confirmación a través de la aplicación PHPsimpex, se tiene lo siguiente:

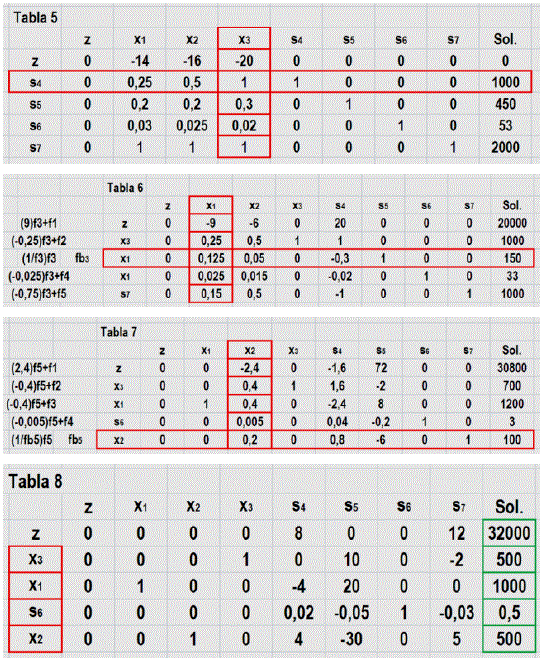
Fuente: Elaboración propia, edición captura de pantalla hoja Excel

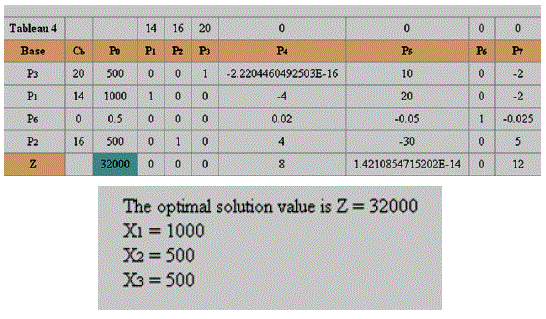
Fuente: [7]

El nuevo resultado establece lo siguiente:

•       Capacidad de envasado limitante 1000 Kg, distribuida así; 1000 bolsas de 0,25 Kg, 500 bolsas de 0,5 Kg y 500 bolsas de1Kg.

•       Las modificaciones en los coeficientes para el tiempo de llenado y la pérdida de producto por peso, mejoran el rendimiento de envasado (250 bolsas más peso 1Kg).

•       Bajo estas condiciones ahora la variable de holgura es (slack variable, s₆ = 0,5). Variables que puede reducirse aun más para mejorar el rendimiento de envasado.

•       Mezcla productiva (0,25 - 0,5 - 1) Kg maximizada con un valor de 32000 unidades monetarias. Incremento del 19 porciento manteniendo los costos de producción invariables[13] y aumentando notablemente el envasado de bolsas con peso de 1 Kg.

Segundo ejemplo:

Restricciones signos igual (=), menor o igual (<), mayor o igual (>), Asignación óptima de recursos para mezclas de materia prima con diferentes características de calidad:

Una empresa beneficiadora de minerales de plata en la ciudad de Potosí - Bolivia, recibe de tres minas aledañas minerales de plata (Ag₂S argentita) de baja ley mezclado con (galena PbS) y esfarelita (sulfuro de plata ZnS). Minerales que se caracterizan por su composición en Ag, Pb, Zn y precio de compra. Ver cuadro 1.

Cuadro 1

Datos del problema

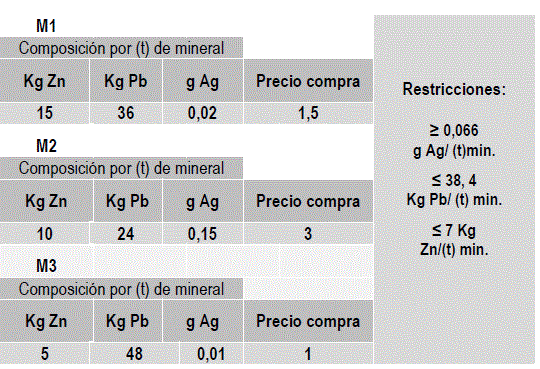
Fuente: Elaboración propia

En consecuencia, se busca determinar las cantidades de estos minerales que se deben mezclar por tonelada, para que cumpliendo con un máximo en la composición de plata, sea mínimo el contenido de plomo y zinc, maximizando el precio de compra de estos minerales. El programa lineal estándar para este problema se representa por:

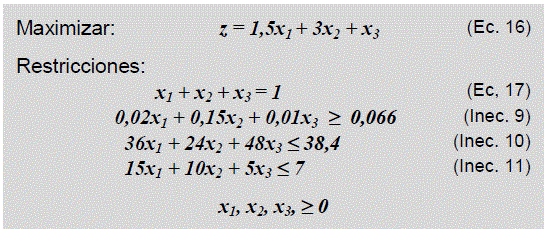
Fuente: Elaboración propia

Soluciones

a) Great M method (Método de la gran M)[14][13], [14]

Tratamiento agregado de programación lineal (PL) que permite desarrollar algoritmos simplex de acuerdo con los signos (=) y (>) de las inecuaciones, incluyendo para el cambio de éstas a ecuaciones, variables auxiliares (s) y artificiales (R). Siendo estas últimas afectadas por el factor (M) que representa a una cantidad muy grande.

Las variables artificiales al no ser parte de la (PL) original, requieren ser igualadas a cero en el momento que se alcance la iteración óptima.

Conversión a ecuaciones e inclusión de variables de holgura auxiliares y artificiales.

Fuente: Elaboración propia sobre información de [13], [16]

Las restricciones y función objetivo del problema dos, de acuerdo con esta reglamentación están representadas por las ecuaciones 18 a 22 y sus coeficientes se muestran en la tabla A:

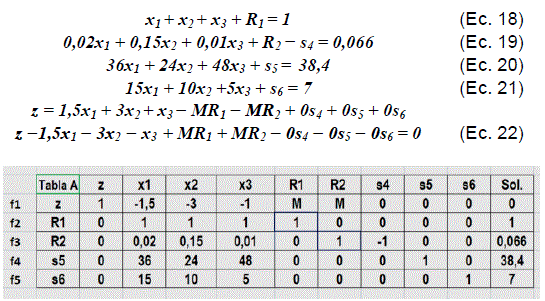
Fuente: Elaboración propia, edición captura de pantalla hoja Excel

Por regla del método de la gran M, las variables artificiales R1 y R2 deben ser convertidas a cero y cumplir con la matriz identidad, por lo tanto es necesario plantear una serie de operaciones involucrando a las otras filas de la tabla A. En este caso multiplicando las filas 1 y 3 respectivamente por (-M) y sumando la fila 1 se llega al cambio exigido:

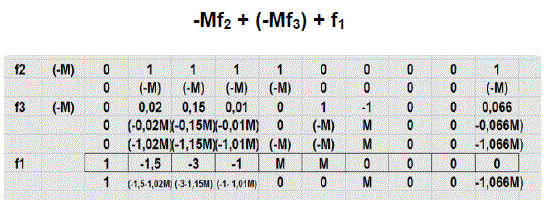
Fuente: Elaboración propia, edición captura de pantalla hoja Excel

Efectuado este cambio en la fila 1, el desarrollo de la PL aplicando el algoritmo simplex, se muestra en las tablas

A, B y C. La casilla con línea verde es parte de la columna de balanceo (permutas: x₂ por R₂, x₃ por R1) y define la fila cociente menor (Sol./columna de Balanceo). Llegando a la solución (x₁ = 0) (x₂ = 0,4) (x₃ = 0,6) y (z = 1,8) iterando dos veces desde la tabla A.

Fuente: Elaboración propia, edición captura de pantalla hoja Excel

Para confirmar que el factor (M) representa ser una cantidad muy grande, sustituyéndole por (1,00E+06) en la tabla A, reporta un resultado similar para la tabla C.

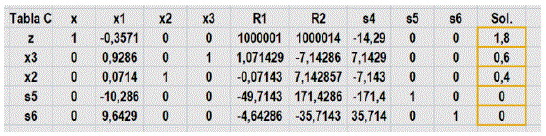
Fuente: Elaboración propia, edición captura de pantalla hoja Excel

Análisis de los resultados problema dos

De acuerdo con este resultado, el óptimo en la función objetivo se puede lograr mezclando los minerales de las minas 2 y 3 en proporciones (0,4-0,6 respectivamente)[15], que maximiza el precio de compra de estos minerales con relación al contenido de plata.

b) Método de las fases [15], [16]

Fase I busca encontrar la solución factible básica inicial, y una vez encontrada, completa la PL con la Fase II para resolver el problema original.

• Fase I. De acuerdo con el signo de las inecuaciones se incorporan las variables de holgura, auxiliares y artificiales (exactamente como en el método de la Gran M). Las variables artificiales contribuyen a formular una función objetivo equivalente (r = Σ R) y para la construcción de las tablas el valor de R será negativo para desarrollo del algoritmo simplex de maximización y positivo para la minimización de la función objetivo inicial. Si el desarrollo del algoritmo conduce a r = 0, el problema tiene solución factible, y se completa el problema en la fase II.

• Fase II. Se incorpora en la tabla precedente de la fase I, los coeficientes de la función objetivo inicial cambiándoles el signo. Finalmente la conversión a matriz identidad en las variables asignadas a través de operaciones auxiliares de apoyo que permiten obtener la solución final.

Aplicando estas normativas a los datos del problema dos, la conversión de las inecuaciones a ecuaciones y la incorporación de variables establecen lo siguiente:

Transfiriendo los coeficientes a la TD se tiene:

Fuente: Elaboración propia, edición captura de pantalla hoja Excel

Para convertir los coeficientes de las variables artificiales R1 y R₂ en ceros (matriz identidad), las operaciones auxiliares para este caso corresponde a sumar las filas f₃+ f₂ + f ₁ .

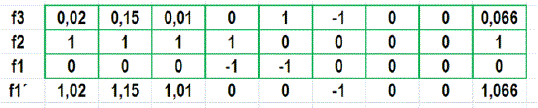
Fuente: Elaboración propia, edición captura de pantalla hoja Excel

Por lo tanto la nueva fila f₁ incorporada en la tabla TD cambiando además sus signos por tratarse de un PL de maximización es:

Fuente: Elaboración propia, edición captura de pantalla hoja Excel

Desarrollando sobre esta tabla el algoritmo simplex, identificación columna y fila de balanceo inicial se tiene la tabla TF y posteriormente la tabla TG:

Fuente: Elaboración propia, edición captura de pantalla hoja Excel

Esta última tabla muestra que r = 0, por lo tanto el PL tiene una solución factible, situación que permite retirar las variables artificiales e introducir en la fila f1 la función objetivo inicial y proceder a convertir los coeficientes a ceros (matriz identidad)[16]a través de operaciones auxiliares, para este caso, corresponde (3f₃+ f₂ + f₁):

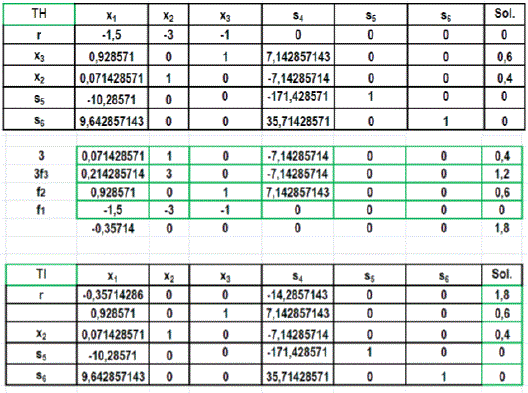
Fuente: Elaboración propia, edición captura de pantalla hoja Excel

Solución utilizando la aplicación PHPsimplex

De manera similar esta aplicación utiliza el método de las dos fases, confirmando el resultado obtenido aplicación php simplex.

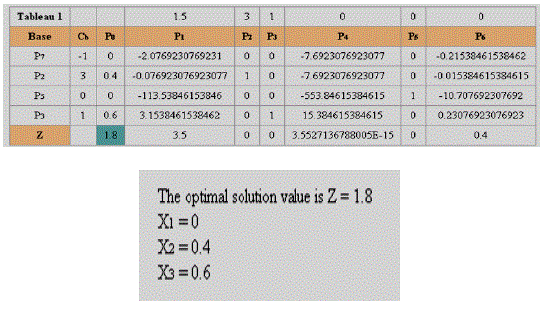
Fuente: [7]

Tercer ejemplo:

Dualidad: A cada PL en las variables (x₁, x₂, x₃,... x_n) toca, asociado, otro PL de variables (w₁, w₂,... w_m) donde (_m) es el número de restricciones del PL original. Siendo este PL el dualdel programa original o primario [17], [18], [19]. Si:

DUALES ASIMÉTRICOS

Fuente: Elaboración propia, sobre información de [17]

 

DUALES ASIMÉTRICOS

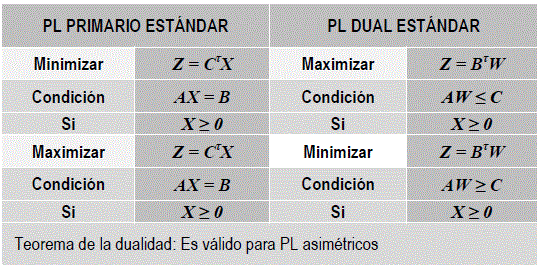
Fuente: Elaboración propia, sobre información de [17]. [18], [19]

PL original distribución de productos: Una empresa que distribuye y comercializa bolsas para despachar productos de supermercado fabricadas de polietileno biodegradable, ha importado 1200 rollos de bolsas (país 1) y 1000 rollos de bolsas (país 2). Toda esta producción debe ser enviada a tres supermercados de la ciudad (diferentes distancias de recorrido) en cantidades de 1000, 700 y 500 rollos, respectivamente. Si el costo de envío por rollo hasta los tres supermercados es:

Cuadro 1

Datos del problema

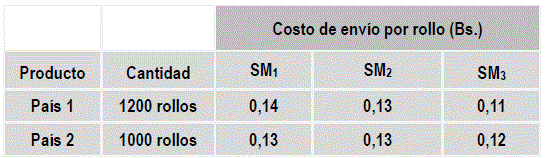
Fuente: Elaboración propia, problema 3 MIIF

Determinar una mezcla de productos óptima según el inventario total de 2200 rollos de costo mínimo.

Planteamiento del PL en forma estándar:

Fuente: Elaboración propia, problema 3 MIIF

P3a) Métodos de las dos fases

Z = 0,14x1P1 + 0,13 x2P1 + 0,11x3P1 + 0,13x4P2 + 0,13x5P2 + 0,12x6P2 +R7 + R8+R9 + R10 + R11

r = 0x1P1 + 0x2P1 + 0x3P1 + 0x4P2 + 0x5P2 + 0x6P2 +R7 + R8+R9 + R10 + R11 = 0

R7 a R11 = 1 criterio de minimización

Con todos estos datos la tabla de inicio para aplicar el algoritmo simplex es:

Fuente: Elaboración propia, edición captura de pantalla hoja Excel problema 3 MIIF

En esta primera fase, para llevar a cero R7 a R11 (matriz) identidad) la operación corresponde a:

{[(-1)f5+f4+f3+f2]+f1}

En la tabla 1 se incorpora esta operación y además se identifican la columna y fila de balanceo con el elemento casilla de intersección:

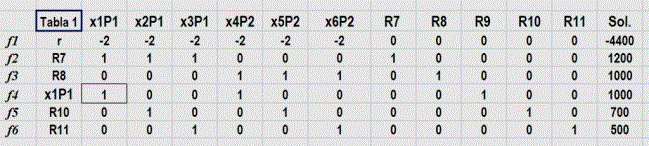
Fuente: Elaboración propia, edición captura de pantalla hoja Excel problema 3 MIIF

Prosiguiendo con la iteración identificando columna y fila de balanceo del algoritmo simplex para llegar a r = 0, ver tablas 2, 3,4, y 5.

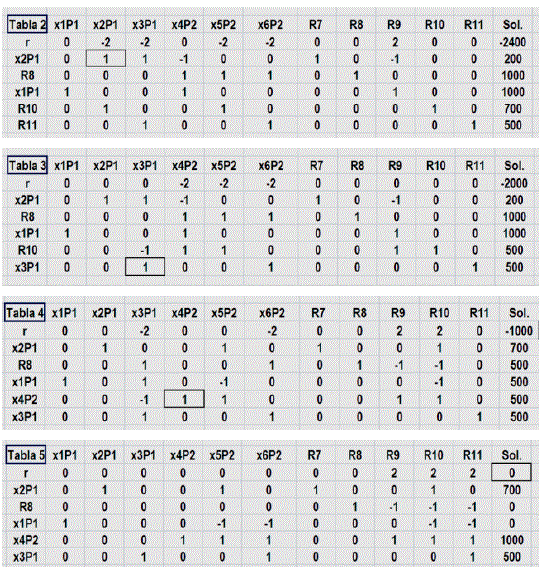
Fuente: Elaboración propia, edición captura de pantalla hoja Excel problema 3 MIIF

Pasando a la segunda fase, al incorporar los coeficientes de la función objetivo original en la fila 1 y no tomando en cuenta las variables artificiales R7 a R11, la tabla 1 IIF recoge los siguientes datos:

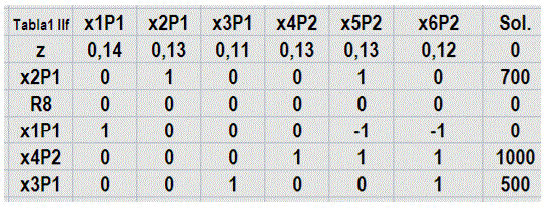
Fuente: Elaboración propia, edición captura de pantalla hoja Excel problema 3 MIIF

Anulando estos coeficientes (matriz identidad) aplicando la operación:

[-1[0,14(f4) + 0,13(f2) + 0,11(f6) + 0,13(f5)] +f1[17]

Concluye la iteración del algoritmo simplex con los datos siguientes:

Fuente: Elaboración propia, edición captura de pantalla hoja Excel problema 3 MIIF

Por lo tanto si:

x2P1 = 700, x1P1 = 0, x4P2 = 1000, x3P1 = 500, x5P2 = 0yx6P2 = 0

Los envíos para cada supermercado según el país de importación indican lo siguiente:

x1P1 + x4P2 = 1000, rollos supermercado 1

0 +1000 = 1000 P2 x2P1 + x5P2 = 700 rollos supermercado 2

700 +0 = 700 P1

x3P1 + x6P2 = 500 rollos supermercado 3 500 + 0 = 500P1

Minimizando el costo de envío a:

Z = 0,13(700) + 0,13 (1000) + 0,11(500) =276Bs.

El análisis combinatorio para este PL con once variables (cinco reales y seis artificiales), más cinco restricciones, establecen 462 combinaciones. Correspondiendo a la solución óptima, la obtenida por el algoritmo simplex verificable a través del desarrollo matricial siguiente:

Fuente: Elaboración propia, edición captura de pantalla Excel desarrollo matricial P3a para el sistema de cinco ecuaciones

P3b) PL Dual

Esta función objetivo puede ser obtenida por el PL dual asimétrico de acuerdo con:

En consecuencia El PL dual estándar es:

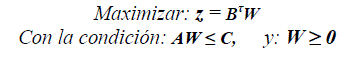
Cambiando fila por columna, la función objetivo dual y las restricciones toman en cuenta los coeficientes:

Z = 1200w1 +1000 w2 + 1000w3 + 700w4 + 500w5

w1+ w3< 0,14

w1 + w4< 0,13

w1+ w5< 0,11

w2 + w3< 0,13

w2+ w4< 0,11

w2 + w5< 0,13

Convirtiendo a ecuaciones e incluyendo las variables de holgura slacks variables (s) que definen al signo menor o igual (<):

w1 + w3 + s6 = 0,14

w1+w4+s7 = 0,13

w1+ w5 + s8 = 0,11

w2 + w3 + s9 = 0,13

w2+ w4+s10 = 0,13

w2 + w5+s11=0,12

Para desarrollar el correspondiente algoritmo simplex, la tabla de inicio T0P3-D es:

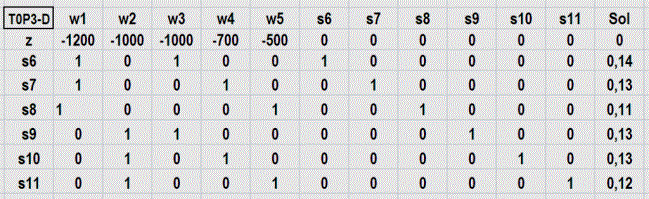
Fuente: Elaboración propia, edición captura de pantalla hoja Excel problema 3, PL - DUAL

Prosiguiendo con las iteraciones T1P3-D a T5P3-D5 se obtiene el mismo valor para la función objetivo PL primaria y PL dual (teorema de la dualidad); y las variables asignadas al problema 3 por el método de las dos fases aparecen en la primera fila casillas slacks variables s7, s8 y s9.

Fuente: Elaboración propia, edición captura de pantalla hoja Excel problema 3, PL - DUAL

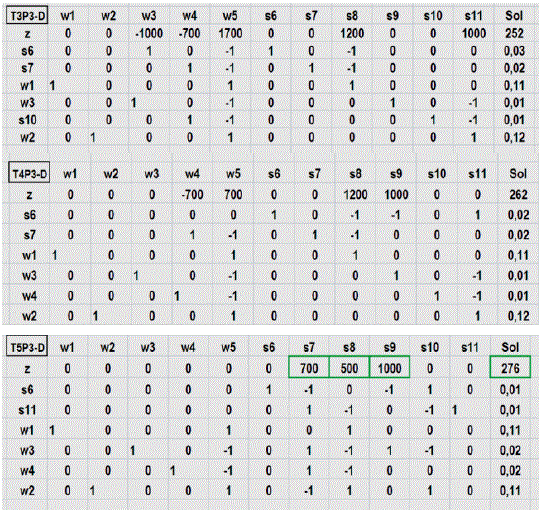
Fuente: Elaboración propia, edición captura de pantalla hoja Excel problema 3, PL - DUAL

Evaluando (z) a partir de los valores encontrados para w1, w2, w3, w4, y w5

Z = 1200w1 + 1000 w2 + 1000w3 + 500w4 + 700w5

Z = 1200(0,11) +1000(0,11) + 1000(0,02) + 700(0,02) + 500(0)

Z = 276

El análisis combinatorio para este PL con once variables (cinco reales y seis artificiales), más seis restricciones, establecen también 462 combinaciones. Correspondiendo a la solución óptima, la obtenida por el algoritmo simplex verificable a través del desarrollo matricial siguiente:

Fuente: Elaboración propia, edición captura de pantalla Excel desarrollo matricial P3a para el sistema de cinco ecuaciones

La importancia de este resultado permite comparar frente al promedio de estos costos de envío, cálculo que por lo general se considera cuando no se tiene la información disgregada. Siendo el promedio de los costos 0,1267 Bs. y este valor afectando el total del número de rollos 2200, reporta 278,67 Bs. Estableciendo una diferencia de 2,67 Bs., que para fines de un mayor volumen de envíos es significativo, y además aporta con una mejor información para la toma de decisiones al respecto.

Cuarto ejemplo:

Programación entera y acotación

Un programa entero es un PL que exige obtener una solución con cifras enteras y que todas las variables sean enteras. Por lo tanto, se puede iniciar el algoritmo simplex o alguna de sus variantes preliminares según el signo de las inecuaciones como una primera aproximación, y resolviendo el PL obtener un resultado sobre el cual se pueden efectuar redondeos de cifras, bifurcaciones y acotaciones que permiten desarrollar un nuevo algoritmo en busca de una segunda aproximación que tiene una determinada desviación porcentual respecto a la primera aproximación, pero que concluye con una solución óptima factible. [20], [21], [22]

a)P4

Aplicación a un problema con dependencia entre el volumen y peso de cinco productos sólidos de forma cúbica con lados diferentes, que deben ser introducidos en cinco contenedores de capacidades 130 cm³ (1), 149 cm³ (1) y 110 cm³ (3), que en conjunto pueden alcanzar 609 cm³ en volumen y 300 g en peso. Buscando obtener el máximo en la función objetivo (relación: volumen/peso) a través de la selección de cuáles cubos y en qué cuantía deben ser colocados estos cubos al interior de los cinco contenedores.

Primera aproximación:

Fuente: Elaboración propia, edición captura de pantalla Excel desarrollo PL P4' primera aproximación

Las tablas T0-P4´, T1-P4´y T2-P4´ muestran el desarrollo del algoritmo simplex.

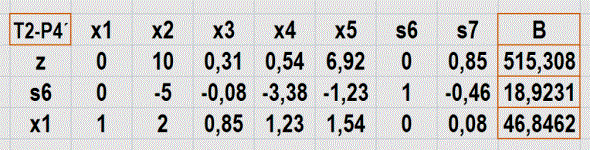
Fuente: Elaboración propia, edición captura de pantalla Excel desarrollo PL P4' primera aproximación

Discusión del resultado P4' y segunda aproximación:

• Considerando este resultado, sólo se llenarían los contenedores con el sólido cúbico x₁ en un número entero de 46. Sin embargo, de acuerdo con las condiciones físicas de los contenedores y el volumen del sólido cúbico x₁ = 13 cm³ se pueden llenar los tres contenedores de 110 cm³con 24 cubos y en el caso de los contenedores de 130 y 149 cm³ con 10 y 11. Por lo tanto sólo se pueden introducir 45 cubos dejando un equivalente en volumen libre de 24 cm³ (609-585), en consecuencia sobre este resultado real, la función objetivo corresponde a (45 x11) = 495, reduciendo además el peso en 30 g.

Sin embargo, acotando algunas variables, la nueva PL considera lo siguiente:

Fuente: Elaboración propia

Según el signo de las inecuaciones (≤) y la orden de maximizar, la tabla de inicio corresponde a:

Fuente: Elaboración propia, edición captura de pantalla Excel desarrollo PL P4 segunda aproximación

Prosiguiendo con las tablas T1P4 a T6P4:

Fuente: Elaboración propia, edición captura de pantalla Excel desarrollo PL P4 segund aproximación

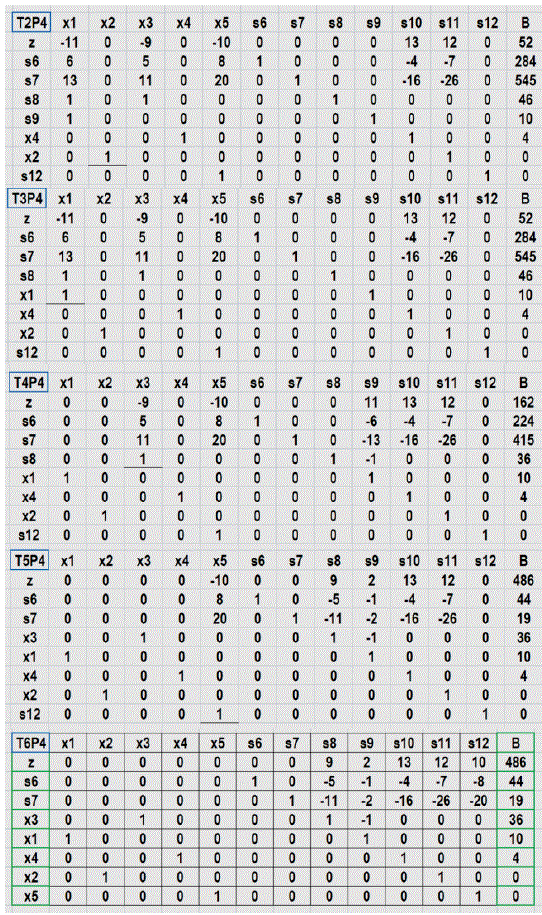
Fuente: Elaboración propia, edición captura de pantalla Excel desarrollo PL P4 segunda aproximación

Confirma este resultado el desarrollo matricial 7x7 para la resolución de este sistema de ecuaciones, considerando 12 variables (v): cinco reales (e) y siete de holgura (s). De una combinatoria [12!/ 5!(12-5)!] = 792 opciones.

Fuente: Elaboración propia, edición captura de pantalla Excel desarrollo matricial PL P4 segunda aproximación

A partir de los resultados de la tabla T6P4, la mezcla de sólidos cúbicos que optimizan la función objetivo es:

En la figura 4 se muestra la mejor disposición física de sólidos cúbicos en los cinco contenedores, tomando en cuenta la reducción del peso (15 porciento) y la cobertura máxima del volumen (96,8%) totales, con la consecuente función objetivo (486) estandarizada.

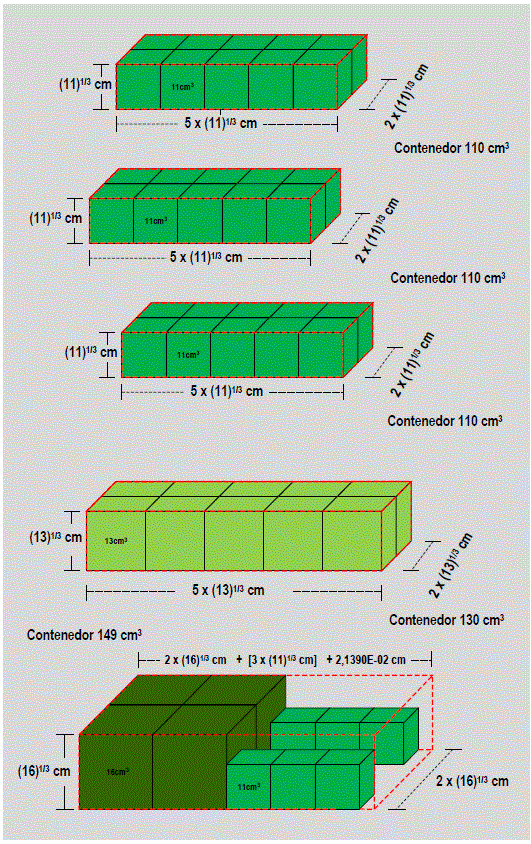
Fuente: Elaboración propia

Figura 4: Disposición física de sólidos cúbicos en cinco contenedores, problema 4 segunda aproximación

En variedad de casos el cambiar desde una PL inicial no entera hacia otra entera; debido a la inclusión de acotaciones, bifurcaciones (alternativa mayor y menor que acota las restricciones), además del redondeo de la parte decimal, ocasiona que el valor de la función objetivo tenga una deviación respecto al valor de la PL original. En estos casos si bien no se tiene un óptimo muy bien definido, el resultado puede ser considerado en general como un estándar, modelo, norma, patrón o referencia, en problema reales de optimización de PL.

En consecuencia, respecto al problema propuesto, por la forma de los contenedores y el volumen de los sólidos cúbicos, además de la imposibilidad de fraccionarlos, la solución estándar pertenece a la mostrada en la figura 4.

Principales áreas actuales de aplicación (As) y (PL)

Al tomar en cuenta una característica en común que se requiere distribuir o mezclar considerando un modelo lineal de comportamiento, las principales aplicaciones corresponden a operaciones de:

•      Producción (asignación óptima de recursos en general, control de inventarios).

•      Administración (planificación movimientos y transportes, inversiones).

Temas adicionales de PL más complejos y algoritmo simplex

•      Flujo capacitado de costo mínimo, formulación de PL y algoritmo simplex de red capacitada. (Resolución de problemas de transporte).

•      Algoritmo de descomposición de Danzing-Wolfe.           (Divide un problema original en sub problemas).

•      Algoritmo de punto interior de Karmarkar. (Resolución de problemas PL con un gran número de variables, produce soluciones al interior de la región factible).

 

CONCLUSIONES

A través de estos cuatro ejemplos se ha buscado resaltar el objeto de estudio, los principales criterios para desarrollar el algoritmo simplex (AS) y su relación con temas propios de la programación lineal (PL), dualidad, programaciones paramétrica y entera.

Mejorando de esta manera las fuentes de información para una toma de decisiones específica con soporte matemático objetivo y cuantificable; asignando variables implicadas en la optimizando de una función objetivo, que generalmente está ligada a factores económicos que son fundamentales para el desarrollo y sostenibilidad productiva de cualquier emprendimiento actual.

• Objeto de estudio

Toma en cuenta una característica en común que se requiere distribuir o mezclar

considerando un modelo matemático lineal de comportamiento entre sus variables.

•       Principales criterios para aplicar el algoritmo simplex

1.      Representación de Programas lineales tomando en cuenta la función objetivo (maximizar o minimizar), las restricciones y la condición que todas las variables sean positiva.

2.      Factibilidad de dependencia lineal.

3.     Adición de variables básicas y variables auxiliares de acuerdo con los signos de las inecuaciones (caracterización de restricciones).

4.      Elaboración de tableaux (tablas de iteración):

4.1.    Simplex normal, variables de holgura (s), signo (<).

4.2.    Simplex modificado, variables auxiliares (R y s). Método gran M y procedimiento de dos fases, cuando Las restricciones incluyen signos (=), (>).

5.      Cambios de signo según los coeficientes de la función objetivo (maximización o minimización).

6.      Identificación columnas de balanceo.

7.      Elemento de balanceo resultado menor cociente B/ valor fila de balanceo.

8.      Desarrollo del algoritmo hasta conseguir la condición de parada (stop condition) o cambio de signo en los coeficientes de la función objetivo.

•      Base procedimental aplicativa del algoritmo simplex

Abstrayendo en parte la fundamentación matemática pura y rigurosa de este procedimiento[18]. El algoritmo simplex (AS) fundamenta su aplicación, eligiendo entre los valores de la fila (z) al número negativo más extremo (maximización), o al número positivo más extremo (minimización) y en función a éstos establece la columna de balanceo (cb1) que luego se relaciona con la columna (B) a través del cociente menor B/ valor casillas de la columna de balanceo de la columna de balanceo (cb1). La fila del cociente menor encontrado define la fila de balanceo (fb1), y a la vez identifica el valor de casilla que debe ser convertido a la unidad efectuando el producto con el valor recíproco de la casilla, afectando a todas las otras casillas de la fila de balanceo (fb1).

Obtenida la unidad para la casilla de la fila de balanceo, la nueva fila (fb₁') sirve para operar con los valores de las casillas de la columna de balanceo cambiando su signo para de esta manera obtener los correspondientes ceros.

La tabla J sirve de inicio para operar el procedimiento fundamental del algoritmo simplex, convirtiendo los valores de la columna de balanceo en una columna de ceros y uno:

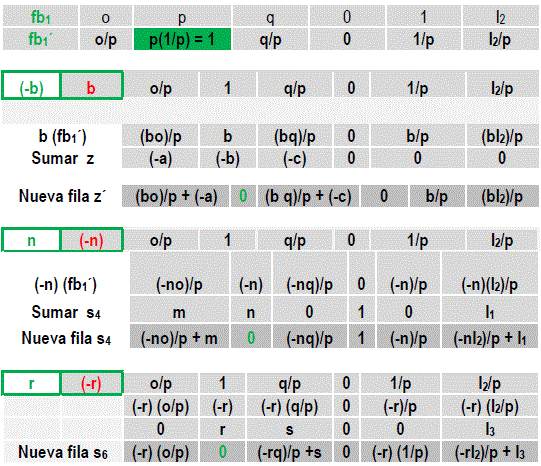
Efectuadas las conversiones la tabla J cambia para dar paso a la tabla K, donde la variable x₂ ha sido asignada como importante para la función objetivo en cumplimiento a la normativa de convertir los valores de la columna en ceros y la unidad.

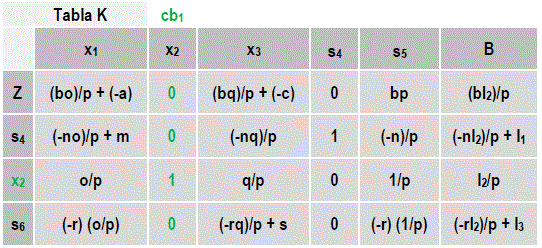
Esta nueva tabla K, permite repetir (iterar) el procedimiento en busca de las columnas y filas de balanceo que identifiquen a las variables significativas que optimicen la función objetivo propuesta. Resultado que se puede obtener en tiempo real utilizando sistemas computacionales sin importar el número de variables básicas y de restricciones.

• Relación con la Programación Lineal (PL)

Ejemplo uno: PL y algoritmo simplex, PL y programación paramétrica (cambios en los parámetros del modelo determinando la nueva solución y su análisis de sensibilidad en la función objetivo.

Ejemplo dos: PL y algoritmo simplex e inclusión de variables artificiales.

Ejemplo tres: PL y algoritmo simplex, soluciones primales y duales.

Ejemplo cuatro: PL y algoritmo simplex, introducción a la programación entera, solución obtenida considerando variables reales enteras. Para determinar la solución estándar, el procedimiento toma en cuenta la acotación, incorporando nuevas restricciones para cada variable de decisión (acotar) que al ser evaluadas independientemente (ramificar) conducen al óptimo entero.

 

Notas

[1] Acción y efecto de optimizar (buscar la mejor manera para realizar una actividad),

[2] También denominado criterio de calidad.

[3] Límite superior o extremo al que puede llegar algo. (DRAE).

[4] Límite inferior o extremo al que se puede reducir algo. (DRAE).

[5] Desigualdad algebraica que separa sus términos (incógnitas e independientes) ya no por el signo (=), y lo hace más bien por los signos (<) menor que, (>) mayor que, (<) menor o igual que, (>) mayor o igual que. Se le atribuye al matemático húngaro Gyula Farkas (1902). el método para resolver sistemas de inecuaciones con múltiples soluciones https://hmong.es >Farkas' lemma

[6] Parte de la ciencia administrativa soportada por métodos matemáticos de análisis sobre modelado, inferencia estadística y principalmente optimización que contribuyen con información para elegir una mejor toma de decisiones al momento de ejecutar determinada actividad productiva, de administración o de gestión. [2]

[7]Propuesto por el matemático norteamericano Bernard George Dantzig en 1947, fue elegido como uno de los diez algoritmos más importantes del siglo XX que influyeron en el desarrollo de la ciencia y tecnología [mbrjournal.com > 2021/01/26 > george-bernard-dantzig The Pioneer of Linear Optimization]. Sin embargo, en 1939 un algoritmo similar de programación lineal, orientado hacia la maximización de la productividad, las materias primas y el trabajo, fue propuesto por el economista y matemático ruso Leonid Vitaliévich Kantoróvich, que en 1975 compartió con el economista de origen holandés Tjalling C. Koopmans el premio Nobel de economía por sus investigaciones sobre la asignación óptima de recursos escasos. El resultado de ambos algoritmos, expresado en el algoritmo simplex, actualmente sirve para solucionar problemas de investigación operativa de (m) restricciones y (n) variables. [http://nobelprize.org/nobel _prizes/economics/laureates/1975/kantorovich-autobio.html]

[8][https://es.wikipedia.org/w/index.php?title=Algoritmo símplex&oldid= 140626542]

[9]Hewelt Packard HP-48, HP- 50, Casio 9860 incorporan en su menú (PL) simplex.

[10]Conjunto descentralizado de puntos de comunicación que se interconectan a través de la geografía mundial. Ofrece además de otros servicios (telefonía, correo electrónico) la consulta remota de archivos en hipertexto a través de grupos de protocolo WWW (World Wide Web) comúnmente páginas Web.

[11]

[12]El procedimiento iterativo desarrollado en Excel utilizó 405 operaciones (productos, cocientes y sumas).

[13] z = 14(1000) + 16(500) + 20(500) = 32000

[14]GM method es un procedimiento agregado de PL que tiene sus limitaciones debido a los errores de redondeo. Usándose en su remplazo el método de las dos fases.

[15]Ag: 0,4[0,15g/ (t) min.] + 0,6[0,01 g/ (t) min.] > 0,066g/ (t) min.]

Pb: 0,4 [24Kg/(t) min.] + 0,6[48g/(t) min.] < 38,4Kg/(t) min.]

Zn: 0,4 [10Kg/(t) min.] + 0,6[5g/(t) min.] < 7Kg/(t) min.]

Z = (1,5)0,4+ (1)0,6 =1,2+ 0,6 = 1,8

Mezcla: 400 Kg M2 + 600 Kg M3 = 1000 Kg nuevo mineral cumpliendo con las restricciones establecidas

[16]Matriz cuadrada de orden n donde todos sus elementos son ceros menos los elementos de la diagonal principal. Cumple las propiedades de ser un elemento neutro del producto de matrices por lo que el producto de cualquier matriz por la matriz identidad no tiene efecto.

[17]

[18]Para comprender mejor los principios matemáticos del algoritmo simplex, acceder al libro Dantzig, G., 1988 Linear programming and extentions, 11 edition, Chapters: 5 Simplex method and two phases, 7 Duality, 8 Pivot element 10 Parametric programming 11 interger programming, Princeton University, NY-USA, https://books.google.com.bo/books?¡d=2¡46uCX5ZAYC&printsec=frontcover&source=qbs q e summarv r&cad=0#v=onepage&q&f=false

 

BIBLIOGRAFÍA

Fundamentos Programación lineal (PL) y algoritmo simplex (AS)

Ventzel, S. E., 1983, Investigación de operaciones problemas, principios, metodologia, Capitulo 3 Programación lineal, Ed. Mir, Rusia,        [ Links ]

Gonzales, G. J.A, 1976, Técnicas operativas para la toma de decisiones, Primera parte Contexto cierto - programación lineal, ISBN: 84-7087-160-9, Ed. INDEX, Madrid - España,        [ Links ]

Dantzig, B.G., M. Thapa, 1997, Linear programming 1: Chapter 3 simplex method, Springer - Verlag, Serie operations research Stamford University. USA,        [ Links ]

Dantzig, G., 1988 Linear programming and extentions, 11 edition, Chapters: 5 Simplex method and two phases, 7 Duality, 8 Pivot element 10 Parametric programming 11 interger programming, Princeton University, NY-USA, Obtenido de: https://books.google.com.bo/books?id=2j46uCX5ZAYC& printsec=frontcover & source=gbs_ ge summarv r& cad=0#v=onepage& q& f=false

Ficken, A., 1961, The simplex method of linear programming. Chapter: 7 The simplex method tableaux, Chapter 8 effectiveness of the simplex method, Dover edition, 2015, NY-USA, Obtenido de: https://books.google.com.bo/books/about/The_ Simplex Method of LinearProgramming.html?id=E152CQAAQBAJ& redir_ esc=y.        [ Links ]

Referencias bibliográficas:

Sistematización Programación lineal (PL) y algoritmo simplex (AS)

[1]Tíjonov, A., Kostomárov, D., 1987, Conferencias de introducción a las matemáticas aplicadas, Capítulo 6: Problemas de optimización

Programación lineal método gráfico, Ed. Mir, Rusia,

[2] Vian, O. Á., 1969, El pronóstico económico en Química industrial, Apéndice Métodos especiales de optimización, Ed. Alhambra segunda edición, p: 265, Madrid - España,        [ Links ]

[3] Bronson, R., 1990, Teoría y problemas de Investigación de operaciones, Capítulo 1 Programación matemática, p:1, Serie de compendios Schaum, Mac Graw-Híll, ISBN: 968-451-385-2, primera edición 1982, México,        [ Links ]

[4] Simplex method theory http://www.phpsimplex.com/en/simplex method theory.htm

[6] Resolución programación lineal (PL) utilizando el algoritmo Simplex, http://www.simplexme.com/de/

[7] Resolución programación lineal (PL) utilizando Simplex two phases method, http://www.phpsimplex.com/simplex/simplex.htm?l=en

[16] Simplex two phases method, Ejemplo dos http://www.phpsimplex.com/simplex/simplex.htm?l=en

[5] Bronson, R., 1990, Teoría y problemas de Investigación de operaciones, Capítulo 4 Programación lineal, el método simplex, p: 34, Serie de compendios Schaum, Mac Graw-Híll, ISBN: 968-451-385-2, primera edición 1982, México,        [ Links ]

[14] Bronson, R., op.cit., Cap. 4, Método M, pp: 35 -41,        [ Links ]

[17] Bronson, R., op.cit., Cap. 5, Dualidad, pp: 45-53,        [ Links ]

[20] Bronson, R., op. cit., Cap. 6, Programación entera y acotación, pp: 54- 60,        [ Links ]

[8] Hillier, F., Lieberman, G., 2010, Investigación de operaciones, Novena edición formato PDF, ISBN: 978- 607-15-0308-4, Algoritmo simplex en forma tabular, Cap.4, p: 94,        [ Links ]

[9] Idem, Aplicación análisis de sensibilidad, Cap. 6, p: 206,

[10] Ibidem, Programación lineal paramétrica, Cap. 7, p: 259,

[18] Hillier, F., Lieberman, G., op. cit., Cap. 6, Relación primal-dual pp: 189-193,        [ Links ]

[22] Hillier, F., Liberman, G., op. cit., Cap. 11, programación de restricciones pp: 476 - 480,        [ Links ]

[11] Taha, H.A., 2012, Investigación de operaciones, Capítulo 3, Análisis de sensibilidad algebraica. Función objetivo, p: 123, Novena edición, Pearson Educación, México, ISBN: 978-607-32-0796-6, Área: Matemáticas,        [ Links ]

[12] Taha, H.A., op. cit Cap. 7, Programación lineal paramétrica, p: 294,        [ Links ]

[13] Taha, H.A., op. cit., Cap 3 Método M, pp: 89-93,        [ Links ]

[15] Taha, H.A., op. cit., Cap.3 Método de las dos fases pp: 89 - 93,        [ Links ]

[19] Taha, H., op. cit., Cap. 4, Definición del problema dual, Relaciones primal-dual. pp: 137-141,        [ Links ]

[21] Taha, H. A., op. cit., Cap. 9, Programación lineal entera, pp: 315-335.        [ Links ]