ARTÍCULO DE INVESTIGACIÓN

 

Modelo de ojiva normal de dos parámetros: una alternativa para
el análisis de instrumentos de medición

 

 

Dr(c). Chocotea Poca, Omar^1,2 & Lic. Villa Cabero, Dafne Maritza^3
1 Instituto de Estadística, Universidad de Valparaíso, Chile.
² Carreras de Estadística/Sociología, Universidad Mayor de San Andrés
Bolivia omar.chocotea@postgrado.uv.cl
³ Carreras de Ingeniería Comercial/Financiera, Escuela Militar de Ingeniería
Bolivia mvilla@doc.emi.edu.bo

 

 

---

Resumen

Los modelos de la Teoría de Respuesta al ítem, TRI, (ítem Response Theory, en inglés) son una alternativa más eficiente frente a la Teoría Clásica de los Test, TC o TCT, para el análisis de la calidad técnica de instrumentos de medición. Comparada con la TC, la TRI permite obtener más información sobre los ítems de la prueba y sobre el constructo o variable latente que interesa medir en los examinados; sin embargo, hay todavía problemas de estimación no resueltos, que provocan algunas veces, la imposibilidad de ajustar ciertos modelos en conjuntos específicos de datos. El presente artículo centra su atención en presentar la teoría del modelo de ojiva normal de dos parámetros, donde los parámetros y también el rasgo latente juegan un papel importante. Dadas las ventajas del modelo, el problema se encuentra en elegir el mejor método de estimación de los parámetros, al ser un modelo no lineal, se deben utilizar procesos iterativos de simulación. Las estimaciones de los parámetros fueron obtenidas mediante el método de simulación de Monte Carlo vía Cadenas de Markov (Markov Chain Monte Carlo: MCMC) en WinBUGS, donde las correspondientes corridas se hicieron en BRugs, que es una librería de R. Una vez obtenidos los valores de las estimaciones de los parámetros se pueden obtener las probabilidades de respuesta del ítem dado el rasgo latente del estudiante, las respectivas Curvas Características del Ítem, Función de Información de la prueba y Error Típico de Información. Para esta aplicación se utilizó el examen del curso de verano 2005.

Palabras claves Medición, Psicometría, Teoría de respuesta al ítem, Análisis de ítems, Estimación de modelos.

---

Abstract

Models of item response theory, IRT (Item Response Theory, in English) are more efficient compared to the Classical Theory Test, TC or TCT, for the analysis of the technical quality of measuring instruments alternative. Compared with CT, TRI allows more information ontest items and on the construct or latent variable of interest measured in examinees; however, there are still unresolved problems estimate, causing sometimes impossible to adjust certain models in specific datasets. This article focuses on presenting the theory model warhead normal two parameters, where the parameters and the latent trait also play an important role. Given the advantages of the model, the problem lies in choosing the best method of parameter estimation, being a nonlinear model, you must use iterative simulation processes. The parameter estimates were obtained by the method of Monte Carlo simulation via Markov Chain (Markov Chain Monte Carlo: MCMC) in WinBUGS, where the corresponding runs were made in Brugs, which is a library of R. Once obtained values of the parameter estimates can be obtained probabilities item response given student latent trait, the respective Item Characteristic Curves, Test Information Function and Standard Error Information. For this application the examination of the summer course 2005 was used.

Keywords Measurement, Psychometrics, Item response theory, Item analysis, Model estimation.

---

 

 

1. INTRODUCCIÓN

El origen de la TRI es antiguo, data de los años cuarenta del siglo pasado, en pleno apogeo de la TC (ver Lawley, 1940,1944). No obstante, dada la complejidad e imposibilidad de llevar a cabo los cálculos requeridos para las estimaciones, no comenzó a difundirse y utilizarse hasta la generalización de los ordenadores con amplias capacidades de cálculo. La razón de su éxito y rápida expansión radica en que permite analizar aspectos de los test que no son posibles o son difíciles de justificar bajo la TC.

1.1.  TEORÍA DE RESPUESTA AL ÍTEM.

Una forma de establecer las relaciones entre las medidas observadas y el constructo es relacionando con éste las puntuaciones de cada uno de los ítems y por medio de los patrones de las respuestas obtener una estimación del valor del sujeto en el constructo. Esta aproximación se refleja en un O. Chocotea & M. D. Villa conjunto de modelos etiquetados de forma general como la TRI.

1.2.  CARACTERÍSTICAS

Bajo el nombre genérico de la TRI se agrupan muchos modelos distintos. Aunque se diferencian en algunos aspectos, todos tienen en común una serie de rasgos básicos, especialmente el de ser modelos estructurales que establecen una relación matemática formalizada entre la respuesta a un ítem concreto y el nivel de rasgo o aptitud de un sujeto. El hecho de presentar un conjunto de aspectos comunes es lo que hace que aparezcan como un cuerpo teórico unificado. A continuación, se mencionan los postulados básicos que caracterizan a los modelos de la TRI:

a) Parten de la existencia de rasgos o aptitudes latentes que permiten predecir o explicar la conducta de un examinado ante un ítem de un test. La TRI parte de la premisa de que el comportamiento de un sujeto ante un ítem puede explicarse en términos de una o varias características del sujeto denominadas rasgos o aptitudes latentes, que no pueden observarse directamente. Por ejemplo, la puntuación de un sujeto en un test de inteligencia (comportamiento observable) es resultado o función de una aptitud o rasgo (inteligencia) que posee el sujeto y que no podemos observar, pero que se manifiesta a través de ciertas conductas (respuestas a los ítems del test).

b) La relación entre el rendimiento o la conducta de un examinado en un ítem y el conjunto de rasgos responsables de dicho rendimiento pueden describirse mediante una función monótona creciente, denominada función característica del ítem o curva característica del ítem (CCI).

1.3.  CURVA CARACTERÍSTICA DEL ÍTEM

Mediante ella se representa una relación funcional entre la proporción de respuestas correctas a un ítem y el nivel del atributo. En general, y por razones de sus orígenes en los test de aptitudes, el rasgo suele denominarse aptitud, aunque conviene indicar que el rasgo puede ser cualquier atributo o constructo en el que se manifiesten diferencias individuales, tales como rendimientos académicos, variables de personalidad, actitudes, intereses, etc., no limitándose los modelos a la inteligencia y rendimiento académico. En adelante nos referiremos a estos indistintamente como rasgo, aptitud o atributo.

1.4.  VENTAJAS DE LOS MODELOS DE LA TRI.

Al cumplir un conjunto de supuestos los diferentes modelos de la TRI, los cuales se describen líneas más abajo, estos poseen una serie de ventajas sobre la TC y que se derivan de los procedimientos de estimación que utilizan:

a)  Los modelos de la TRI, a diferencia de los de la TC, son falsables. En cualquier aplicación de la TRI es esencial evaluar el ajuste del modelo a los datos.

b)  Los ítems pueden ser descritos por unas propiedades o parámetros que se pueden estimar.

c)  Asumiendo la existencia de un amplio universo o población de ítems para la medida del mismo rasgo, la cantidad de rasgo que posee un sujeto particular es independiente del conjunto concreto de ítems utilizado en su estimación.

d)  A diferencia de la TC que caracteriza la precisiónpormediodeunúnicovalorparatodo el conjunto de puntuaciones (el coeficiente de fiabilidad), la TRI la caracterizará por medio de una función denominada función de información, que indicará cómo son de precisas las puntuaciones en los diferentes niveles de aptitud.

1.5. SUPUESTOS

Unidimensionalidad

De forma general se asume que hay un conjunto de rasgos responsables de la actuación del examinado en la prueba, el cual define un espacio dimensional latente y pudiendo representarse en el la posición de cada uno de los examinados y de los diferentes ítems. Sin embargo, en las aplicaciones de la TRI se supone que una única aptitud o rasgo es suficiente para explicar los resultados de los examinados y las relaciones entre los ítems.

Independencia local

La independencia local significa que si se mantienen constantes las aptitudes que explican el rendimiento de la prueba, las respuestas de los examinados a un par de ítems cualesquiera, son estadísticamente independientes. La independencia local se deriva de la unidimensionalidad ya que simplemente significa que la respuesta a un ítem solo depende de sus parámetros ya que no está influida por el orden de presentación de los ítems. Cuando se cumple el supuesto de unidimensionalidad, se obtiene la independencia local. En este sentido, los dos supuestos son equivalentes (ver Lord, 1980; Lord&Novick, 1968).

 

2. MODELO

Sea y_ij una variable aleatoria que representa la respuesta binaria de un examinado i (i <= n) en el ítem j (j <= k). Para una respuesta correcta y_ij = 1, y para una respuesta incorrecta y_ij = 0. Suponiendo un espacio latente unidimensional (ver por ejemplo Villa, 2006, p. 25), la probabilidad de responder correctamente está dada

donde Φ(•) denota la función de distribución acumulada de la distribución normal estándar, y q_i(θ) = 1 - p_j(θ_i).

Sea

entonces, la función de verosimilitud es

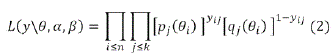
La información concerniente a los parámetros de interés θ,α y β es contenida en la distribución a posteriori de estos parámetros, y esta es

donde la densidad conjunta π(θ,α,β) es la distribución a priori del vector de parámetros θ,α y β. También asumiremos independencia entre los parámetros, es decir

De acuerdo con Vega (2006), asumiremos que

 

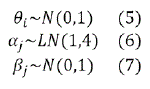
3. APLICACIÓN

3.1. DESCRIPCIÓN DE LOS DATOS

Ilustremos el análisis con los datos de la prueba tomada en el curso de verano de la Carrera de Informática a la asignatura Estadística II el 2005. La evaluación se efectuó a 117 estudiantes, con un total de 12 ítems, donde se llega a tener 12 dificultades, 12 discriminaciones y 117 rasgos latentes.

Entonces, nuestrabase de datos es especificada por el marco de datos, de algunas variables que pueden llegar a ser las más importantes para poder medir la discriminación que llega a tener la habilidad. Con respecto a la edad, la edad mínima es de 19 años y la edad máxima es de 35 años, son 80 hombres y 37 mujeres, la mayoría egreso del colegio que se encuentra en la ciudad (108), y 51 trabajan. El más antiguo que ingreso a la carrera lo hizo en 1990 y los nuevos ingresaron el año 2003, 49 estudiantes aprobaron del colegio particular y 66 del fiscal, los que si aprobaron la materia de Matemática son 72 y los que no aprobaron son 45 estudiantes.

3.2. FORMULACIÓN DEL PROBLEMA

Dado el modelo (1), donde se tiene que hallar la probabilidad de respuesta del ítem dadas las habilidades de los estudiantes, para luego poder hallar las CCI de los ítems, la curva característica de la prueba, y las funciones de respuesta del ítem y la función de información de la prueba. Para luego poder hallar las funciones de respuesta de la prueba.

3.3.  ESTIMACIÓN DE LOS PARÁMETROS DE LOS ÍTEMS

Utilizando WinBugs y BRugs se obtienen las siguientes estimaciones, primeramente para los parámetros para luego poder tener el de la habilidad, donde no se toman todos los valores de la estimación (ver Vega, 2006).

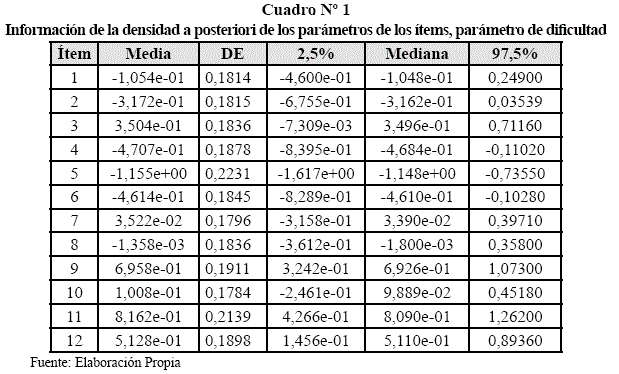
La dificultad más alta corresponde a ₁₁= 0,8162 y el ítem más sencillo 11 corresponde ₅ = -1,155, según el Cuadro N° 1 de toda la prueba.

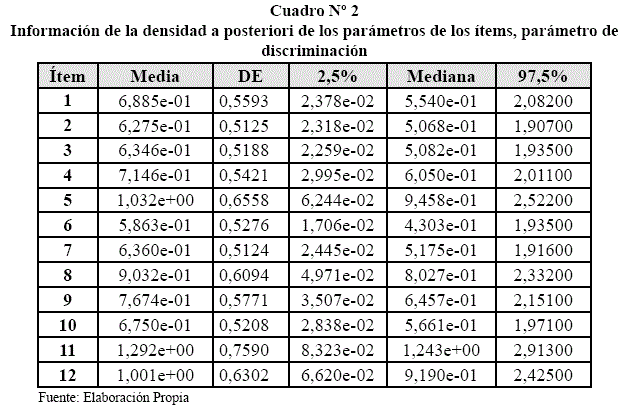
En el Cuadro N° 2 se pueden observar las estimaciones de los parámetros de discriminación, donde los ítems más discriminatorios son los siguientes, ₁ = 1,292 con una mediana de 1,243 que llega a ser la más alta, ₁₂= 1,001 con una mediana de 0,9190, ₅ = 1,032, los menos discriminatorios son ₂ = 0,6275, ₁= 0,9032 y ₄= 0,7146 que tiene una mediana de 0,6050.

3.4. ESTIMACIÓN PUNTUAL DELA HABILIDAD

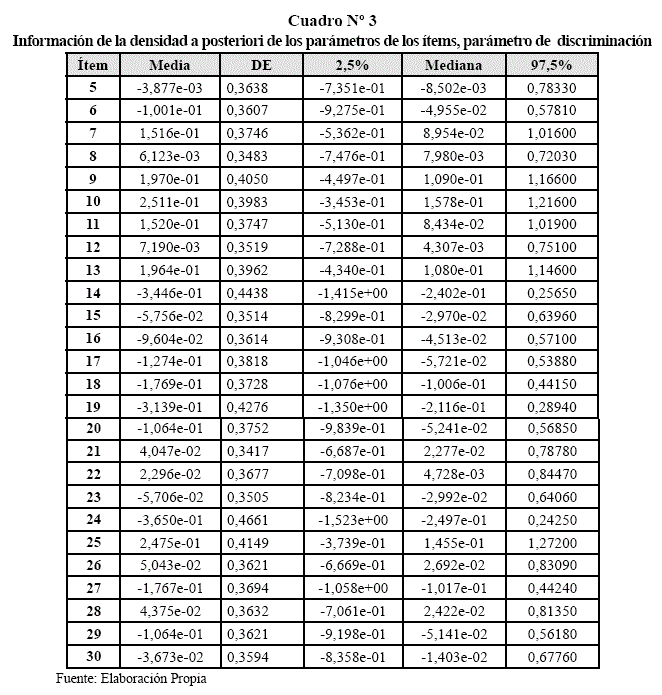
Los valores encontrados en el Cuadro N° 3, reflejan que ₃₀=-0,03673 es un poco más hábil que ₂₉ = -0,1064 pero ambas habilidades no A son muy buenas como ₂₂ = 0,1520 que llega a ser la más alta habilidad de este Cuadro pero se tiene la habilidad más alta de la prueba que corresponde a ₅₇ = 0,4328 (ver Vega, 2006).

3.5. ANÁLISIS DEL PARÁMETRO DE DISCRIMINACIÓN

La Figura N° 2 del nuevo modelo que se llama habilidad y que llega a ser nuestro parámetro de discriminación, con respecto a la edad, se ha dividido la edad en cuatro grupos donde se puede ver que el grupo de los jóvenes tiene más habilidad que el grupo de los mayores y también se ve que se tiene más alumnos con habilidades altas entre las edades de 19 y 23 años.

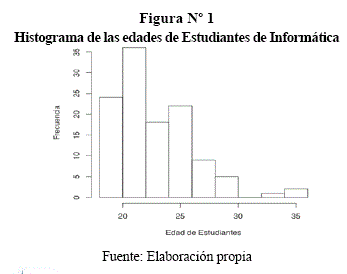
Se tiene en la Figura N° 1 el total de edades de los estudiantes del curso de verano de la gestión 2005, la materia de Estadística II, de la Facultad de Ciencias Puras y Naturales.

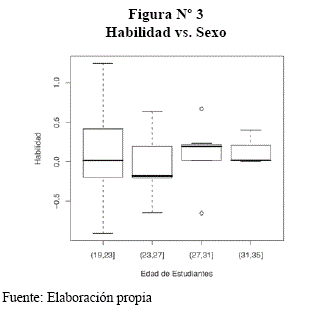
Se tiene a la habilidad con respecto al sexo y se puede ver que los hombres son más hábiles que las mujeres según la figura del boxplot de la habilidad ya que la mediana de los hombres es mayor que de las mujeres con el sexo según la Figura N° 3.

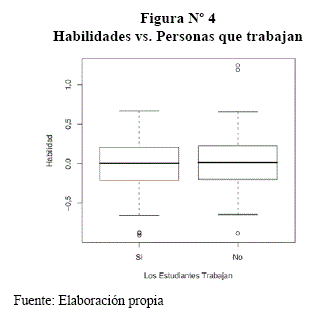
Ahora en la Figura N° 4, a aquellos estudiantes que trabajan con respecto a la habilidad y se nota que no existe diferencia significativa entre ellos.

Ahora en la Figura N° 5, si la administración del colegio afecta de alguna manera en la habilidad del estudiante y se nota que los colegios de administración pública son los que tienen un poco más de habilidad con respecto a los de colegios particulares pero no tiene mucha diferencia significativa.

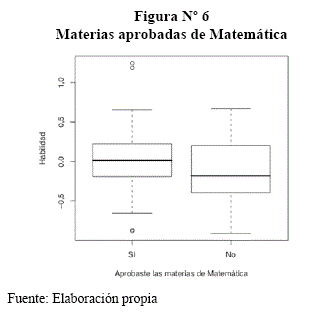
Cómo se puede apreciar en la Figura N° 6, la mayoría de los estudiantes aprobaron todas las materias de matemáticas, lo cual puede llegar a influir en la habilidad de cada uno de los estudiantes.

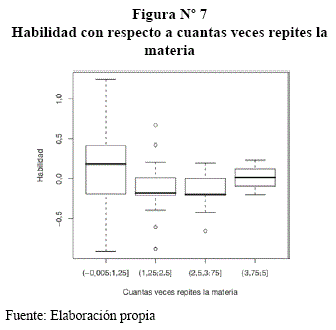
El haber reprobado con más de una ves dice mucho que sea una persona hábil, y la Figura N° 7 refleja que cuanto más veces repites una materia tienes un poco mas de habilidad para poder aprobar el curso.

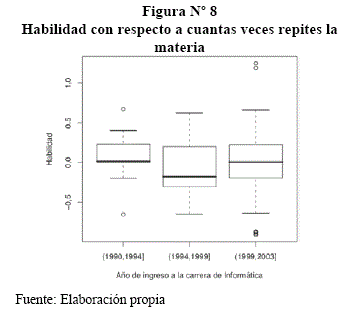
Se puede ver que los estudiantes que ingresaron entre los años 1990-1997, llevan un poco más de ventaja en relación a los que ingresaron entre los años 1997-2003, pero los que tienen mas habilidad llegan a ser los de los años 1997-2003, eso muestra la Figura N°8.

3.6. CURVAS CARACTERÍSTICAS

Curvas características del ítem (CCI)

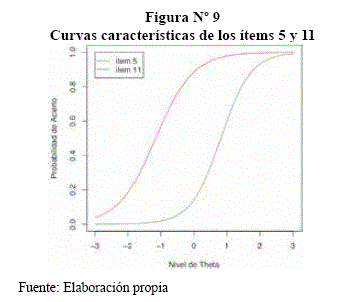
Se tiene las curvas características de los ítems 5 y 11, donde se tiene dos ítems con menor y mayor dificultad. Y se ve que elítem de color rojo corresponde al ítem 5 y llega ser el mas fácil de toda la prueba, el de color verde corresponde al ítem 11 que es el más difícil. Donde ambos ítems llegan a ser los más discriminantes de toda la prueba según la Figura anterior y de sus respectivas estimaciones.

Se elige al azar dos estudiantes con habilidad θ₂₅=0,2475, donde tiene una probabilidad de responder el ítem 5 de aproximadamente 0,92 que es el ítem más sencillo, pero para el ítem 11 que es el más difícil será de 0,25 aproximadamente. Ahora para la habilidad negativa de θ₅₈ = -0,3722 la probabilidad de respuesta para el ítem difícil será de 0,35, para el ítem fácil es de 0,75 aproximadamente.

Las probabilidades de acierto para θ₁ = 0,1640 del ítem 1 es de 0,51, para el ítem 2 es de 0,62, del ítem 3 es 0,41 y para el ítem 4 será de 0,69, por lo que el ítem más difícil corresponde al ítem 3.

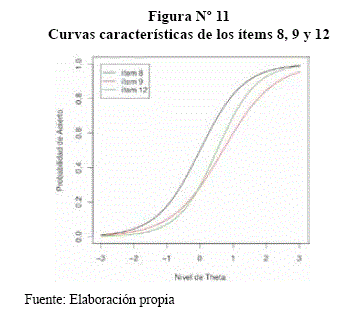
Para poder determinar probabilidades de respuesta para θ₁₅=-0,05756, donde el ítem 8 será respondido con una probabilidad de 0,44, el ítem 9 con una probabilidad de 0,21 y la misma probabilidad para el ítem 12.

Curva Característica de la Prueba (CCP)

El papel CCP es proporcionar un procedimiento para poder transformar las puntuaciones de habilidad en puntuaciones verdaderas.

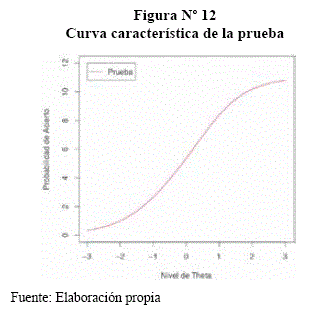
La CCP predice las habilidades de los estudiantes, cuantas respuestas serán las correctas, también hace posible realizar estimaciones a priori.

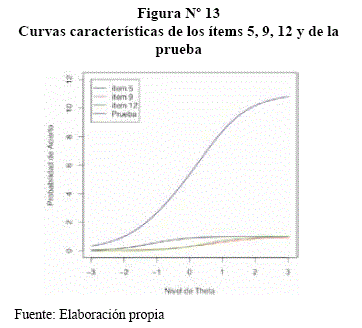
3.7. FUNCIONES DE INFORMACIÓN

Función de Información del Ítem (FII)

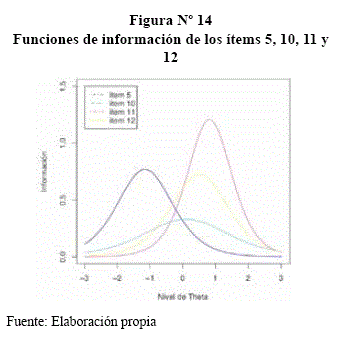
El ítem 11 aporta con mayor información con una θ ≈ 1, el de menor información corresponde al ítem 5.

La mayor información corresponde al ítem 9 y al ítem 3 para una θ ≈ 1.

Función de Información de la Prueba (FIP)

La FIP es la curva más alta que de los ítems por que mide en forma general.

Se ve claramente que es mayor la FIP a los ítems 5, 9, 11 y 12. Donde siempre la FIP será mayor que la FII.

Error típico de estimación

Conceptualmente este error típico ET(9), no es un estadístico, sino una función de a. Para una prueba cualquiera se tiene muchos errores típicos de estimación. Con este concepto, dejan tener utilidad los conceptos de fiabilidad y de generalizabilidad de una prueba, ya que una prueba puede ser fiable, tener un poco error en ciertos niveles de a y poco fiables en otros. Para los datos de aplicación, los errores típicos de estimación en los diferentes niveles de θ son los siguientes,

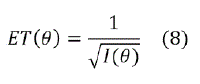
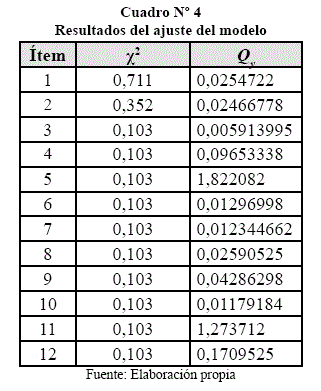
3.8. AJUSTE DEL MODELO

Para los modelos de la TRI, se tiene muchos métodos de ajuste o de bondad de ajuste a los datos, del tipo chi-cuadrado. El que se utiliza es el método de ajuste Q_y de Yen (1981).

El estadístico de se distribuye según una chi-cuadrado con m - k grados de libertad donde m es el número de intervalos en que se dividió la aptitud y k* es el número de parámetros del modelo. Si el valor del estadístico de Yen (1981), supera el valor crítico de X²_{m-k*,1- α}se rechaza la hipótesis nula de que la CCI se ajusta a los datos. Cuando se tiene muchos ítems que no se ajustan, podemos sospechar que se ha elegido un modelo inadecuado e intentar reanalizar los datos bajo otro modelo alternativo.

Como se ve en el Cuadro N° 4 la mayoría de los ítems se ajustan a Q_y, pero el ítem 5, como el ítem 11 no se ajustan. Para la prueba se tiene que Q_y= 3,52 tiene que ser menor al calculado X²_{m-k*,1- α} = 3,940. Por lo tanto, la prueba se ajusta.

 

4. CONCLUSIONES Y RECOMENDACIONES

4.1. CONCLUSIONES

El modelo de ojiva normal de dos parámetros es un modelo que ayuda a resolver una serie de problemas en la medición educacional. La principal ventaja que ofrece esta teoría es la invarianza de los parámetros que describen los ítems (dificultad, discriminación), y de los parámetros que describen a las personas. La utilización del modelo de ojiva normal de dos parámetros en el campo de la evaluación educacional es sin duda un aporte significativo que facilitara y perfeccionara la tarea de diseño e implementación de pruebas, especialmente aquellas de gran escala.

El modelo de ojiva normal de dos parámetros nos permite un ajuste adecuado a los datos, quedando atrás los métodos tradicionales, pues nos permite llegar a conclusiones claras de acuerdo con los objetivos del estudio. El empleo del método MCMC, resulta de mayor importancia a la hora de obtener resultados confiables, se aplico WinBUGS y BRugs. Cuando se utiliza TRI, es muy difícil para un profesor predecir el puntaje que tendrá un alumno en la prueba real, ya que lo más seguro es que no tendrá los parámetros de las preguntas que él mismo ha diseñado para el ensayo, ni las herramientas para estimar el puntaje a partir de éstos.

4.2. RECOMENDACIONES

TRI es una teoría que se funda en una serie de supuestos que se cumplan. Es importante evaluar que los supuestos se cumplan de manera adecuada, es decir, éstas no sean tan importantes como para invalidar las aplicaciones de TRI y afectar significativamente la propiedad de invarianza de los parámetros. Para ello, es fundamental que expertos en el tema realicen las pruebas adecuadas para testear si efectivamente se está cumpliendo la unidimensionalidad y si el modelo está ajustándose a los datos experimentales. Por ejemplo, si se detecta que un determinado tipo de pregunta es fuente de multidimensionalidad, se debe evaluar el efecto desde el punto de vista del contenido y propósitos del test, y cuáles serían los efectos de su eliminación. Es posible que en muchos casos sea preferible cambiar el modelo estadístico a utilizar antes que desechar definitivamente el tipo de pregunta. Es muy importante que los expertos encargados de implementar el modelo estén al tanto de las nuevas investigaciones y vayan avanzando juntamente con los progresos que se vayan dando en la teoría.

 

Agradecimientos

El primer autor fue parcialmente apoyado por la beca FIB-UV de la Universidad de Valparaíso, de Chile. Los autores agradecen al editor por sus útiles comentarios.

 

Apéndice

 

BIBLIOGRAFÍA

Lawley, D. N. (1940). VI.—the estimation of factor loadings by the method of maximum likelihood., "Proceedings ofthe Roy al Society ofEdinburgh", 60(1), 64-82. 1        [ Links ]

Lawley, D. N. (1944). X.—the factorial analysis of multiple item tests. "Proceedings ofthe Royal Society ofEdinburgh. Section A. Mathematical andPhysicalSciences", 62(1), 74-82. 1        [ Links ]

Lord, A. B. F. M. (1980). "Applications of Item Response Theory to Practical Testing Problems".Lawrence Erlbaum Associates. 3        [ Links ]

Lord, A. B. F. M. & Novick, M. R. (1968). "Statistical Theories of Mental Test Scores". Addison-Wesley Publishing Company. 3        [ Links ]

Vega, G. F. (2006). "El modelo logístico de dos parámetros". Tesis de Licenciatura, Universidad Mayor de San Andrés, La Paz. 3,4,5        [ Links ]

Villa, M. D. (2006). "El modelo rasch y aplicaciones". Tesis de Licenciatura, Universidad Mayor de San Andrés, La Paz. 3        [ Links ]

Yen, W. M. (1981)., "Usingsimulationresults to choose a latent trait model". Applied Psychological Measurement, 5(2), 245-262. 10        [ Links ]