ARTÍCULO

 

Distancia a la frontera tecnológica y educación: Alternativas de crecimiento económico para países en desarrollo

 

Distance to technological frontier and education: Alternatives for economic growth for developing countries

 

Fernando Velasquez Torrez* Saúl R. Quispe Aruquipa*
* El contenido del presente documento es de responsabilidad de los autores y no compromete la opinión del Banco Central de Bolivia.

 

 

---

Resumen

Analizamos la situación de las economías en desarrollo respecto a su posición en torno a la frontera tecnológica mundial. En base a Vandenbussche et al. (2006) y Acemoglu et al. (2006), presentamos un modelo matemático de crecimiento económico endógeno con capital humano y progreso técnico, relacionado con el resto del mundo por medio de la distancia a la frontera tecnológica. El modelo permite identificar cómo se asignarán los recursos destinados a la inversión en capital humano, de acuerdo a la proximidad de la economía a la frontera tecnológica mundial. Se plantea un modelo dinámico de datos de panel para 121 economías en el periodo 1970-2015. Los resultados muestran que la educación primaria es la que explica la tasa de crecimiento de la productividad total de factores para economías en desarrollo, por lo que se debería aumentar la inversión en este sector.

Clasificación JEL: C33, I20, O40

Palabras clave: Educación, crecimiento económico, capital humano, distancia a la frontera tecnológica, datos de panel

---

Abstract

We analyze the situation of developing economies with respect to their position around the world technology frontier. Based on Vandenbussche et al. (2006) and Acemoglu et al. (2006), we present a mathematical model of endogenous economic growth with human capital and technical progress, related to the rest of the world through distance to technological frontier. The model allows identifying how the resources to invest in human capital will be allocated, according to the proximity of the economy to the world technology frontier. A dynamic model of panel data is proposed for 121 economies in the period 1970-2015. Results show that primary education is what explains the growth rate of total factor productivity for developing economies, so that investment in this sector should be increased.

JEL Classification: C33, I20, O40

Keywords: Education, economic growth, human capital, technology frontier distance, panel data

---

 

 

I. Introducción

Uno de los factores de producción que explican el crecimiento de la productividad de las economías es el capital humano. Sin embargo, como señala Islam (2010) no existe un consenso sobre cómo el capital humano puede ayudar a los países a promover el crecimiento. Esta falta de consenso se ve plasmada en los enfoques teóricos, como en el caso de Lucas (1988) y Mankiw et al. (1992), quienes señalan que la acumulación de capital humano es la principal fuente de crecimiento de la productividad, es decir, la tasa de crecimiento depende de la tasa de acumulación de capital humano y no del nivel de capital humano. Por otro lado, los enfoques que se apoyan en la hipótesis de Nelson y Phelps (1966) sostienen que el stock de capital humano puede aumentar la capacidad de un país para desarrollar su propia innovación tecnológica, y también aumenta su capacidad para adoptar tecnologías desarrolladas en otros países, favoreciendo de esta forma el crecimiento económico. Los modelos de crecimiento endógeno como el de Romer (1990), Aghion y Howitt (2009) y Acemoglu (2002) señalan que el capital humano mejora el crecimiento económico, generando más innovación. La distinción entre los dos tipos de trabajo (calificado y no calificado) es importante para la innovación, como lo señalan Grossman y Helpman (1991). Esto se debe a que en el sector de investigación el capital humano facilita el progreso tecnológico generando nuevas ideas.

Sin embargo, el capital humano, medido por el nivel educativo o el gasto en educación, ha presentado algunos problemas a nivel empírico. Krueger y Lindahl (2001) muestran que las estimaciones del capital humano sobre el crecimiento, no son significativas cuando se consideran los países de la OECD. En relación a esto, Aghion y Howitt (2009) op. cit. plantean una solución a este problema. Estos autores toman como base el modelo de Vandenbussche et al. (2006) para considerar dos casos en los que analizan la composición del stockde capital humano y su relación con el crecimiento. En el primer caso, se distinguen las actividades de imitación e innovación como funciones que dependen de un solo tipo de trabajo, a saber, trabajadores con bajo nivel educativo (trabajadores no calificados) en imitación, y trabajadores con alto nivel educativo (trabajadores calificados) en innovación. Posteriormente, se asume que tanto el trabajo calificado como el no calificado, pueden emplearse en ambas actividades, concluyendo que el efecto del trabajo calificado sobre el crecimiento de la productividad, es mayor cuando la economía está más cerca de la frontera tecnológica; esto ocurre porque cuando se está cerca de la frontera, se requiere mayor innovación, mientras que cuando la economía está alejada de la frontera tecnológica, el efecto del trabajo no calificado es mayor sobre el crecimiento de la productividad (esto ocurre cuando la economía está orientada más a actividades de imitación).

La evidencia empírica (Islam, 2010 op. cit.; Acemoglu et al., 2006, y Madsen, 2014) ha mostrado que en economías desarrolladas, el efecto del capital humano calificado, aumenta con la proximidad a la frontera tecnológica, mientras que el capital humano no calificado está contribuyendo más en los países de bajos ingresos, a medida que se acercan a la frontera tecnológica.

Para contribuir a los resultados empíricos, estimamos un modelo de panel de datos en sistemas y diferencias (Roodman, 2006) para 121 economías (36 economías desarrolladas y 85 economías en desarrollo) para el periodo 1975-2010. Los resultados mostraron que la educación secundaria y terciaria, tienen un efecto positivo y significativo en la tasa de crecimiento de la productividad de factores en las economías desarrolladas, mientras que para las economías en desarrollo la educación primaria tiene un efecto positivo.

El contenido del trabajo es el siguiente: en la segunda sección se desarrolla el modelo matemático de crecimiento y distancia de la frontera tecnológica; en la tercera sección se describen las variables; la cuarta sección comprende la metodología; en la quinta sección se realiza la estimación del modelo econométrico; y por último, las conclusiones.

 

II. Modelo teórico

Para entender la relación entre la productividad total de los factores, la brecha tecnológica y la educación, Nelson y Phelps (1966) parten del postulado teórico de que el progreso técnico es de tipo Harrod, para todos los ratios capital-trabajo, de modo que el progreso puede ser descrito como aumentador de trabajo. Esto se puede representar como una función de producción, donde el producto (Q) es función del capital K, trabajo L y del tiempo t. Matemáticamente:

Q(t) = F[K(t),A(t)L(t)]              (1)

En la ecuación (1) "la variable A(t) es un índice de tecnología, K(t) es el capital actualmente comprado, L(t) es la mano de obra que trabaja con el capital, y Q(t) es la producción. Entonces A(t) mide el nivel de mejor práctica de tecnología. Se podría suponer que la ecuación (1) es la función de producción "agregada" para la empresa, industria o economía y A(t) es el índice medio común a todas las unidades de capital, viejo y nuevo".

Además, estos autores introducen "la noción teórica del nivel de tecnología T(t). Esta se define como el nivel de tecnología de mejor práctica, que prevalecería si la difusión tecnológica fuera totalmente instantánea. Es una medida del stock de conocimientos o técnicas que están disponibles para los innovadores. Supongamos que el nivel tecnológico avanza a una tasa exponencial constante y exógena igual a λ:

T(t) = T₀e^λt, λ> 0                        (2)

Primer modelo. Nelson y Phelps (1966) op. cit., señalan que "elrezago del tiempo entre la creación de una nueva técnica y su adopción, es una función de algún índice de logro educativo medio, h, de aquellos en situación de innovar (h indica el grado de intensidad del capital humano). Denotemos w como el rezago. Se puede representar esta noción como sigue:

A(t) = T (t-w (h)), w'(h)<0                    (3)

El nivel de tecnología en la práctica, equivale al nivel teórico de tecnología w años atrás (w es una función decreciente de h). Substituyendo la ecuación (2) en la (3) tenemos:

A(t) = T_oe^λ(t-w(h))                     (4)

Si h es constante, dos resultados se siguen de (4). Primero, el índice de la tecnología en la práctica, crece a la misma tasa λ, que el índice teórico de la tecnología. Segundo, el "nivel" o la trayectoria de la tecnología en la práctica, es una función creciente h, ya que un aumento de h acorta los rezagos entre T(t) yA(t)".

Este modelo, según Nelson y Phelps (1966) "no es muy satisfactorio, porque no es razonable suponer que el rezago del nivel de mejor práctica, detrás del nivel teórico de tecnología, es independiente de la rentabilidad de nuevas técnicas aun no introducidas. Además, es poco realista suponer que un aumento de los logros educativos reduce instantáneamente el rezago, en ese sentido [estos autores plantean] un segundo modelo más realista".

Segundo modelo. "El segundo modelo establece que la tasa a la cual la tecnología en la práctica es conducida a mejores prácticas tecnológicas, depende del nivel educativo y de la brecha entre el nivel teórico de la tecnología y el nivel de la tecnología en la práctica", [lo que se denota por]:

donde g_λ (t) denota el crecimiento de la productividad total de los factores o el crecimiento del conocimiento, A denota la productividad de los factores y  es el cambio en A. De acuerdo con esta segunda hipótesis de Nelson y Phelps (1966), "la tasa de crecimiento de la tecnología en la práctica (no el nivel), es una función creciente del nivel educativo" y de la brecha entre el nivel teórico de la tecnología y el nivel de tecnología en la práctica; la tasa a la cual se cierre esta brecha dependerá del nivel de capital humano. [Nelson y Phelps, 1966, pp. 71 -73]

II. 1. Tecnología de crecimiento de la productividad tipo Cobb-Douglas

Islam (2010) parte de la suposición del trabajo anteriormente descrito de Nelson y Phelps (1966) y el trabajo de Benhabib y Spiegel (1994) para señalar que la educación es un medio para entender y adoptar nuevas tecnologías (esto corresponde al segundo modelo); asimismo menciona que Vandenbussche et al. (2006) y Aghion et al. (2005) predicen que el capital humano no tiene efectos uniformes sobre la innovación y la imitación para acelerar el progreso tecnológico.

El modelo teórico de Vandenbussche et al. (2006) señala que las empresas intermedias pueden aumentar la productividad, ya sea por imitación de las tecnologías de vanguardia o mediante la innovación de tecnologías existentes en el país. La imitación y la innovación pueden ser realizadas por ambos tipos de trabajadores, a pesar de que la elasticidad de la mano de obra altamente educada, es mayor para la innovación, mientras que la elasticidad de la mano de obra de baja educación, es mayor para la imitación.

Vandenbussche et al. (2006) op. cit. centran la atención en la siguiente clase de funciones de crecimiento de productividad

donde:

u_m,i,t y s_m,i,t: Cantidad de trabajo no calificado y calificado usados en la imitación dentro el sector ien el período t, respectivamente.

u_n,i,t y s_n,_i,_t: Cantidad de trabajo no calificado y calificado usados en la innovación dentro el sector ien el período t, respectivamente.

σ y Φ: Elasticidad del trabajo no calificado en imitación e innovación, respectivamente.

λ > 0 : Mide la eficiencia del proceso general de mejora tecnológica.

y> 0 : Mide la eficiencia relativa de la innovación en comparación con la imitación en la generación del crecimiento de la productividad.

Se asumen además los siguientes supuestos:

Supuesto 1. La elasticidad del trabajo calificado es más alta en innovación que en imitación, contrariamente a la elasticidad del trabajo no calificado (Φ<σ).

Denotamos w_u,tÃ_t-1 y w_s,tÃ_t-1 como el precio corriente del trabajo no calificado y calificado. Entonces, el costo total del trabajo de mejoras en la productividad para la firma intermedia ien el período tes igual a:

Denotamos αt=A_t/Ã_t, que mide la proximidad del país a la frontera tecnológica en la fecha t. Asumiendo que la frontera tecnológica , crece a una tasa constante g, la empresa intermedia resolverá el siguiente problema de maximización:

Tomando en cuenta que todas las empresas enfrentan el mismo problema de maximización, y que hay una unidad de masa de empresas, tenemos:

Tomando en cuenta las condiciones de primer orden para el problema de maximización de (8), haciendo uso de las ecuaciones (9) y (10), y después de calcular la tasa de equilibrio de crecimiento de la productividad:

Aghion y Howitt (2009) establecen lo siguiente:

Lema 1. Definimos¹ . Si los valores de los parámetros son tal que la solución de la ecuación (8) es interior entonces tenemos:

Este lema, junto con el hecho de que h (a) es decreciente en a, dado el supuesto 1, inmediatamente implica lo siguiente:

Proposición 1. Dado el supuesto 1, un incremento marginal de la inversión en alta educación S, mejora el crecimiento de la productividad, tanto más cuando más cerca está de la frontera tecnológica mundial, es decir:

Y el incremento marginal en la inversión de la educación más baja U, mejora el crecimiento de la productividad, tanto menos cuando más cerca está el país de la frontera tecnológica mundial, es decir:

Resumiendo, se tiene el siguiente cuadro:

Cuadro 1: EFECTO DEL TRABAJO SOBRE EL CRECIMIENTO DE LA PRODUCTIVIDAD

Fuente: Elaboración propia con base en Vandenbussche et al. (2006)

Según Aghion y Howitt (2009), la intuición que está detrás de esta proposición puede entenderse mediante el teorema de Rybczynski de comercio internacional. Consideremos un aumento en la oferta de trabajo calificado, manteniendo la oferta de mano de obra no calificada fija y un a dado. Asumiendo que los trabajadores calificados contribuyen relativamente más al crecimiento de la productividad y los beneficios si se emplean en la innovación más que en la imitación (Supuesto 1), la demanda de trabajo tenderá a ser más alta en innovación. Esto lleva a que la productividad marginal del trabajo no calificado se incremente más en innovación que en imitación, y a que un flujo neto de trabajadores no calificados debería moverse de la imitación a la innovación.

Esto mejoraría aún más la productividad marginal del trabajo calificado en innovación, lo que induce cada vez más a una mayor fracción de trabajo calificado a moverse a innovación. Mientras más cerca está una economía de la frontera tecnológica, mayor será el efecto Rybczynski. Esto ocurre con una a alta que incrementa la eficiencia de ambos tipos de trabajo en la innovación respecto a la imitación.

El modelo teórico de Vandenbussche et al. (2006), Aghion et al. (2005) y Aghion y Howitt (2009) asumen dos tipos de trabajo que se diferencian en el nivel de educación. En esta descomposición de habilidades, la educación juega un papel importante: en la actividad productiva, la educación terciaria es más propensa a facilitar la innovación, mientras que la educación primaria y secundaria, facilitan la imitación o difusión de conocimientos ya desarrollados en otros países. Por lo tanto, basándose en esta predicción, estos autores proponen que cuanto más cerca esté un país de la frontera tecnológica mundial, más potenciador del crecimiento será para ese país, invertir en educación terciaria. Por otra parte, cuanto más alejado esté de la frontera, es más conveniente que un país invierta en educación primaria y secundaria para aumentar el crecimiento.

Islam (2010) señala que a medida que la distancia de la frontera tecnológica se reduce, el efecto de crecimiento de la educación terciaria aumenta, mientras que el efecto de crecimiento de la educación primaria y secundaria disminuye. Bajo este argumento, la especificación empírica del modelo de crecimiento endógeno de Vandenbussche et al. (2006) toma la siguiente forma:

Si el coeficiente de a₃ es positivo y significativo, implica que los adultos con educación terciaria son más importantes para el crecimiento en economías que están cerca de la frontera tecnológica.

 

III. Variables del modelo

En el siguiente apartado, se describe la base de datos y los indicadores que se emplearon en la estimación. La muestra abarca información quinquenal de 121 países (36 economías desarrolladas y 85 economías en desarrollo) para el periodo 1975-2010. El tamaño de esta muestra fue determinado por la información disponible y la estrategia de utilizar un periodo razonablemente amplio para observar las variables.

La tasa de crecimiento de la productividad total de factores (PTF) se estimó mediante una función de producción tipo Cobb-Douglas: Y =AK^α L^1-α, donde Y indica el Producto Interno Bruto real (PIB), A es la PTF, K es el stock de capital agregado, L es la fuerza de trabajo agregada y a es la proporción del ingreso que viene del capital que se asume es constante.

Al dividir la ecuación por L se obtiene:y =Aka, donde yes el producto por trabajador y k es el ratio de capital por trabajador. De la anterior ecuación, despejando A obtenemos la siguiente ecuación A = y/k^a.

Para encontrar el valor de la PTF utilizamos, en primer lugar, el PIB real per cápita tomando como año base a 2005, el cual es medido por Penn World Tables (PWT) 7.0. El stock de capital se construye mediante el método de inventarios perpetuos (Caselli, 2005). El valor a es igual a 0,30 para toda la muestra (Islam, 2010, op. cit.).

La ecuación de acumulación del capital es la siguiente: K_it = I_it + (1-δ) K_it-1 donde K es la cantidad de capital, δ la tasa de depreciación constante de 5% (Islam, 2010) e I es el nivel de inversión. Para encontrar el nivel inicial de capital, con el método de inventarios perpetuos, se recurre a la siguiente ecuación: donde g es la tasa de crecimiento de Ien estado estacionario, el cual es medido como un promedio de su tasa de crecimiento.

El capital es medido utilizando la clasificación de Barro y Lee (2013) por nivel de estudio: primaria, secundaria y terciaria (o nivel superior). La distancia a la frontera tecnológica se construyó como el ratio de la PTF del país i, y del de Estados Unidos (Vandenbussche et al., 2006). En cuanto a las variables de control, la inflación (tasa de crecimiento del índice de precios al consumidor), el coeficiente de apertura (ratio entre la suma de exportaciones e importaciones con respecto del PIB), y la proporción del gasto público con respecto al PIB, se tomó como base los datos de la PWT 7.0.

 

IV. Metodología econométrica

El proceso generador de datos de un modelo de datos de panel es escrito como:

En la ecuación (12) existe un efecto dinámico de x en y, donde la velocidad de ajuste es controlado por el rezago de y. El supuesto de la ecuación (13) implica que x no está correlacionado con el pasado, presente, y futuro del valor de v; por tanto, xes una variable estrictamente exógena. Sin embargo, no se descarta la correlación entre x y el efecto individual de η (Arellano, 2003).

Alternativamente, la ecuación (12) puede ser escrita como:

Dy_it = {a-Y)y_it__x+x'J+e_it                    (14)

 

La ecuación (15) es un sesgo del panel dinámico, dado queyit-1 está correlacionada con los términos de perturbaciones después de la transformación. Como y_it-1 está correlacionada con v_it-1, cualquier variable x que no es estrictamente exógena, es potencialmente endógena debido a la correlación con v_it-1

Arellano y Bond (1991) sugieren que las variables dependientes rezagadas en t-2 pueden ser usadas como instrumentos para las ecuaciones en primeras diferencias. Los estimadores GMM² controlan la endogeneidad usando instrumentos internos, en base a los valores rezagados de las variables explicativas. El estimador GMM es como una extensión de la metodología de Variable Instrumental (VI) y tiene ventajas sobre los estimadores convencionales como 2SLS³. 2GMM hace uso de las condiciones de ortogonalidad para permitir una estimación eficiente en presencia de heteroscedasticidad.

Blundell y Bond (1998) muestran que los estimadores GMM en diferencias, pueden estar sujetos a una concentración de muestras finitas sesgadas, especialmente cuando el número de períodos de tiempo es pequeño. Los autores mostraron que cuando las variables explicativas son persistentes en el tiempo, los niveles rezagados de la variable dependiente son instrumentos débiles en primeras diferencias. En estos casos, los problemas graves de identificación, pueden conducir a sesgos y podrían resultar en unos estimadores diferenciados de bajo rendimiento. Arellano y Bover (1995) sugieren el uso de retardos de las series en primeras diferencias, como instrumentos para ecuaciones en niveles. Roodman (2006) recomienda que se utilice 2 rezagos, y que las variables endógenas puedan ser utilizadas como instrumentos en la práctica.

Una restricción importante del estimador, que se corrige con una correcta modelización, es que no exista autocorrelación de segundo orden en las primeras diferencias de los errores. Esta restricción se demuestra con la prueba de Arellano-Bond. La hipótesis nula de esta prueba es la no existencia de autocorrelación, por lo que un valor probabilístico mayor a 0,05 indica la aceptación de esta hipótesis y, por tanto, no existe autocorrelación. La segunda prueba estadística relevante es la de Sargan (1958), con la que se demuestra la existencia de sobre identificación. En esta prueba, la hipótesis nula es que las ecuaciones están correctamente sobre identificadas, por lo que un valor probabilístico mayor a 0,05 indica que la especificación es correcta.

 

V. Análisis Empírico

Utilizando la ecuación (11) se obtiene una ecuación base que se expresa de la siguiente manera:

donde i representa el país y t es el tiempo. La ecuación anterior nos dice que el crecimiento económico de la PTF (g_i,t) es explicado por la proporción rezagada de habitantes con educación primaria (Primi _i,t-1), secundaria (Sec_i,t-1), terciaria (Terc._i,t-1), la distancia a la frontera tecnológica mundial (ln DF_i,t-1) y los efectos multiplicadores de la distancia y la educación. Las variables de control son la inflación (Infi, la apertura comercial (Aperturai,t) y la proporción del gasto de gobierno con respecto al PIB (Gastoi,_i,t). Por último, existe un efecto específico del país, α_i, y un término de perturbación, v_it.

 

V.1 Resultados econométricos

Tras la revisión de la información estadística de las variables (ver Apéndices C y D) se procede a realizar una estimación del modelo planteado anteriormente. Las estimaciones se hicieron para dos grupos de países: países desarrollados y países en desarrollo. El Cuadro 2 resume los resultados de las regresiones utilizando el método de estimación de Roodman (2006) (GMM por diferencias y sistemas).

 

Cuadro 2: DETERMINANTES DE LA TASA DE CRECIMIENTO DE LA PTF, 1975-2010

Fuente: Elaboración propia con el uso de Stata 12.0.

Notas. Los estadísticos t de Student se presentan en letras cursivas. Test de Hansen:

Ho= Las restricciones de sobreidentificación son válidas. AR (1) y AR (2): Ho= No existe autocorrelación.

*** Indica el nivel de significancia del 1% " Ibid., 5%

* Ibid., 10%

La primera columna del Cuadro 2 muestra los resultados de las estimaciones de las variables explicativas de la tasa de crecimiento de la PTF para economías desarrolladas. Los resultados muestran que la educación terciaria tiene un efecto positivo y significativo hacia el crecimiento de la PTF, mientras que la educación secundaria tiene un efecto negativo. Este resultado puede interpretarse como que la población con educación superior, es aquella que ha permitido que estas economías logren mejorar sus niveles de PTF.

Sin embargo, los efectos multiplicativos de la educación y la distancia de la frontera, presentan signos contrarios a los presentados anteriormente, es decir, el efecto multiplicativo de la distancia de la frontera y la educación secundaria es positivo, mientras que la distancia de la frontera y la educación terciaria es negativo. La contrariedad en los signos, podría ser resultado de que al ser países más cercanos a la frontera tecnológica mundial, la población secundaria es la que está llevando a aumentos de la PTF, es decir, que el sector educativo secundario con un grado de tecnología elevado, permitirá que la PTF futura sea elevada.

En el caso de los países en desarrollo, la educación primaria es la que permitió aumentos de la PTF. Sin embargo, el efecto multiplicativo de este sector y su posición en la frontera tecnológica, son negativos hacia la evolución de la PTF. Por tanto, estos resultados muestran que la educación primaria es escasa para alcanzar un elevado crecimiento, por tanto, se debiera aumentar la inversión en este sector para alcanzar rendimientos más elevados.

 

VI. Conclusiones

El crecimiento de una economía, analizado a través de funciones de crecimiento de la productividad, depende de la composición del capital humano, y nos señala que un país que esté dotado en lo que es más importante para crecer, se verá favorecido cuando cambie su proximidad a la frontera tecnológica. Cuando cambia la proximidad de la economía doméstica respecto a la frontera tecnológica, se sigue que es adecuado invertir en trabajo calificado, cuando el mismo está cerca de la frontera tecnológica, y también cuando el trabajo no calificado está alejado de la frontera tecnológica, porque en ambos casos aumentará el crecimiento de la productividad.

En el caso de los estudios econométricos que abordan el tema del crecimiento de una economía y el capital humano, es importante hacer una distinción de la composición de este último, porque si se toma de forma agregada en una regresión, puede arrojar como resultado, ser una variable explicativa no significativa.

Los resultados econométricos indican que en las economías desarrolladas, los impulsores del aumento de la productividad fueron la educación terciaria y el efecto multiplicativo de educación secundaria y la distancia de la frontera. Es decir, que cuanto más próximas estén las economías a la frontera tecnológica, la educación secundaria tendrá un efecto en el aumento de la productividad de los factores. Con respecto a las economías en desarrollo, la educación primaria ha impulsado el crecimiento de la productividad. Este resultado sugiere invertir en la educación primaria para buscar un mayor crecimiento en la productividad total de los factores.

 

Notas

1    Ver el Apéndice A para el desarrollo matemático.

2    Generalized Method of Moments.

3    Two-Stage least squares.

 

Referencias bibliográficas

ACEMOGLU, D. (2002). "Technical Change, Inequality and The Labor Market", Journal of Economic Literature, 40 (1), pp. 7 - 72        [ Links ]

ACEMOGLU, D., P. AGHION, F. ZILIBOTTI (2006). "Distance to frontier, selection, and economic growth", Journal of the European Economic Association, 4 (1), pp. 37 - 74        [ Links ]

AGHION, P., L. BOUSTAN, C. HOXBY, J. VANDENBUSSCHE (2005). "Exploiting State's Mistakes to Identify the Causal Impact of Higher Education on Growth", paper presented at Education Workshop, July 27th, 2005, organized by National Bureau of Economic Research        [ Links ]

AGHION R and P. HOWITT (2009). The Economics of Growth, The MIT Press, United States of America        [ Links ]

ARELLANO, M. and S. BOND (1991). "Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations", The Review of Economic Studies, 58 (2), pp. 277 - 297        [ Links ]

ARELLANO, M. and O. BOVER (1995). "Another look at the instrumental variable estimation of error-components models", Journal of Econometrics, 68 (1), pp. 29 - 51        [ Links ]

ARELLANO, M. (2003). Panel data econometrics, Oxford University Press, United States of America        [ Links ]

BARRO, R. J. and X. SALA-I-MARTIN (1992). "Convergence", Journal of Political Economy, 100 (2), pp. 223 - 251        [ Links ]

BARRO, R. J. and J. W. LEE (2013). "A new data set of educational attainment in the world, 1950-2010", Journal of Development Economics, 104, pp. 184-198        [ Links ]

BENHABIB, J. and M. M. SPIEGEL (1994). "The role of human capital in economic development: Evidence from aggregate cross-country data", Journal of Monetary Economics, 34 (2), pp. 143-173        [ Links ]

BLUNDELL, R. and S. BOND (1998). "Initial conditions and moment restrictions in dynamic panel data models", Journal of Econometrics, 87 (1), pp. 115-143        [ Links ]

CASELLI, F. "Accounting for Cross-Country Income Differences" in AGHION, P. and S. N. DURLAUF (Eds.) (2005) Handbookof Economic Growth, Volume 1A, Handbooks in Economics 22, Elsevier B.V., The Netherlands, pp. 679-741        [ Links ]

EVANS, P. (1996). "Using cross-country variances to evaluate growth theories", Journal of Economic Dynamics and Control, 20 (6-7), pp. 1027-1049        [ Links ]

FEENSTRA, R. C., R. INKLAAR, M. P. TIMMER (2015). "The Next Generation of the Penn World Table", The American Economic Review, 105(10), pp. 3150-3182        [ Links ]

GERSCHENKRON, A. (1962). Economic Backwardness in Historical Perspective: ABook of Essays,The Belknap Press of Harvard University Press, Cambridge, MA, London, England        [ Links ]

GROSSMAN, G. M. and E. HELPMAN (1991). Innovation and Growth in the Global Economy, The MIT Press, London, England        [ Links ]

HOWITT, P. and D. MAYER-FOULKES (2005). "R&D, Implementation, and Stagnation: A Schumpeterian Theory of Convergence Clubs", Journal of Money, Credit and Banking, 37(1), pp. 147-177        [ Links ]

ISLAM, M. R. (2010). "Human Capital Composition, Proximity to Technology Frontier and Productivity Growth", Monash University, Department of Economics, Discussion paper 23/10        [ Links ]

KRUEGER, A. B. and M. LINDAHL (2001). "Education for Growth: Why and for Whom?", Journal of Economic Literature, 39(4), pp. 1101-1136        [ Links ]

LALL, S. (1992). ^“Technological capabilities and industrialization", World Development, 20 (2), pp. 165-186        [ Links ]

LUCAS, R. E. (1988). "On the mechanics of economic development", Journal of Monetary Economics, 22 (1), pp. 3-42        [ Links ]

MADSEN, J. B. (2014). "Human Capital and the World Technology Frontier", The Review of Economics and Statistics, 96 (4), pp. 676-692        [ Links ]

DISTANCIA A LA FRONTERA TECNOLÓGICA Y EDUCACIÓN: ALTERNATIVAS DE CRECIMIENTO ECONÓMICO PARA PAÍSES EN DESARROLLO                                                      31

MAYER-FOULKES, D. (2006a). "Development and Underdevelopment: 1500-2000", mimeo        [ Links ]

MAYER-FOULKES, D. (2006b). "The Impact of Free Trade and FDI: Banana Republic or Miracle Growth?", mimeo        [ Links ]

MAYER-FOULKES, D. (2002). "Global Divergence", Centro de Investigación y Docencia Económicas (CIDE), División de Economía, Working paper, September        [ Links ]

MADDISON, A. (2001). The World Economy: A Millennial Perspective, Organisation for Economic Co-operation and Development (OCDE), Development Centre Studies, Paris, France        [ Links ]

MANKIW, N. G., P. ROMER, D. N. WEIL (1992). "A Contribution to the Empirics of Economic Growth", The Quarterly Journal of Economics, 107(2), pp. 407-437        [ Links ]

NELSON, R. R. and E. S. PHELPS (1966). "Investment in Humans, Technological Diffusion, and Economic Growth", The American Economic Review, 56 (1/2), pp. 69-75        [ Links ]

ROMER, P. M. (1990). "Endogenous Technological Change", Journal of Political Economy, 98 (5), pp. S71-S102        [ Links ]

ROODMAN, D. (2006). "How to Do xtabond2: An Introduction to "Difference" and "System" GMM in Stata", Center for Global Development, Working Paper Number 103, December        [ Links ]

SARGAN, J. D. (1958). "The Estimation of Economic Relationships using Instrumental Variables", Econometrica, 26 (3), pp. 393-415        [ Links ]

THE WORLD BANK (2016). World Development Indicators 2016, Washington D.C.        [ Links ]

VANDENBUSSCHE, J., P. AGHION, C. MEGHIR (2006). "Growth, Distance to Frontier and Composition of Human Capital", Journal of Economic Growth, 11 (2), pp. 97-127        [ Links ]

 

APÉNDICES

Apéndice A

Deducción de la tasa de crecimiento de la productividad

El problema de maximización dado por la ecuación (8) es:

 

Apéndice B

Países de la muestra

Fuente: Elaboración propia con base en Penn World Tables 7.0 y Banco Mundial.

Apéndice C

Descripción estadística: Economías desarrolladas

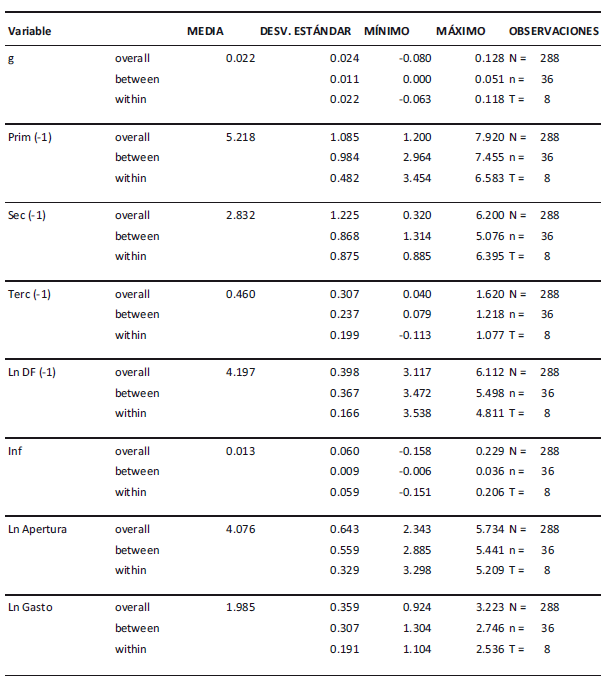
Fuente: Elaboración propia con el uso de Stata 12.0.

 

Descripción estadística: Economías en desarrollo

Fuente: Elaboración propia con el uso de Stata 12.0.

Apéndice D

Correlaciones

Fuente: Elaboración propia con el uso de Stata 12.0.