Servicios Personalizados
Articulo
Indicadores
Links relacionados
 Citado por SciELO
Citado por SciELO
 Similares en SciELO
Similares en SciELO
Bookmark
Revista de Análisis del Banco Central de Bolivia
versión impresa ISSN 2304-8875
Revista de Análisis v.24 n.1 La Paz jun. 2016
ARTÍCULO
Pronóstico de la actividad económica con base en el
volumen transaccional - caso boliviano
Forecast of economic activity based on transaction
volume - Bolivian case
Jonnathan R. Cáceres Santos*
*Correo electrónico del autor: jcaceres@bcb.gob.bo.
Resumen
El objetivo del presente estudio es validar la significancia del volumen transaccional del dinero como una variable que contribuya al pronóstico de corto plazo de la actividad económica en Bolivia.
Para este propósito se emplearon modelos econométricos y de Redes Neuronales Artificiales (RNA). A través de modelos econométricos se halló evidencia empírica soe una relación de largo plazo entre el volumen transaccional y el Índice Global de Actividad Económica (IGAE). Simultáneamente se utilizó el modelo RNA para estimar pronósticos.
Los resultados muestran que ambos tipos de modelos capturaron adecuadamente las fluctuaciones y el comportamiento del IGAE.
Para evaluar la precisión de los pronósticos del IGAE, se tomó en cuenta los errores de predicción dentro y fuera de la muestra. Los pronósticos del modelo RNA registraron errores más bajos en relación a los pronósticos del modelo econométrico.
El presente estudio se constituye en el primero de su naturaleza, puesto que además de evaluar la información contenida en los pagos con dinero electrónico en la economía, la misma se incorpora en modelos de pronóstico anticipando los movimientos futuros de la actividad económica en Bolivia.
Clasificación JEL: C45, C53
Palabras clave: Predicción, redes neuronales
Abstract
The main objective of this document is to validate the significance of the transactional volume of money as a variable that contributes to short-term forecast of economic activity in Bolivia.
For this purpose, econometric and Artificial Neural Networks (ANN) models were used. Through econometric models was found thatthere is empirical evidence of a long-term relationship between the transactional volume and Global Economic Activity Index (GEAI). Simultaneously the ANN model was used to estimate forecasts.
The results show that both models adequately captured the fluctuations and behavior of GEAI.
To evaluate the accuracy of forecasts of the GEAI, the document took into account the forecast errors inside and outside the sample. ANN model forecasts reported lower errors than econometric model forecasts.
This study becomes the first of its kind, because in addition to evaluate the information contained in electronic money payments, this information is also included in the forecast models, thus anticipating future movements in economic activity in Bolivia.
JEL Classification: C45, C53
Keywords: Forecasting, neural networks
I. Introducción
La estimación de los movimientos y cambios futuros que puedan producirse en la actividad económica, es un tema de interés para las autoridades encargadas de la política económica y para los agentes en general. En el primer caso, esta información contribuye a la implementación de medidas anticipadas para que el crecimiento económico sea coherente con las metas previamente establecidas, en tanto que en el segundo caso, posibilita la toma efectiva de decisiones de inversión y consumo.
Debido a la relevancia de esta tarea, analistas e investigadores de bancos centrales, además de otras instituciones del ámbito económico, evalúan información de un conjunto de variables que puedan resultar explicativas de los cambios en el Producto Interno uto (PIB) en el corto plazo1. [Estrella y Mishkin, 1996; Garcés, 2002; oer, 2005]. Usualmente, las variables exógenas incluidas en esta clase de análisis son de carácter financiero, monetario, vinculadas al comercio exterior, o a la producción y/o demanda de determinados bienes y servicios.2
El presente estudio considera que el volumen transaccional de dinero sintetiza información relevante que posibilitaría el pronóstico de corto plazo de la actividad económica, dado que incluye pagos que son realizados en los distintos sectores de la economía por conceptos de gasto de consumo, inversión (pública y privada), demanda externa, demanda de bienes y servicios intermedios, entre otros. Estas transacciones, según corresponda, son realizadas con dinero electrónico procesadas por los sistemas de pago3 y dinero físico (billetes y monedas).
En este sentido, el objetivo del presente estudio es validar la significancia del volumen transaccional de pagos como variable que posibilite el pronóstico de corto plazo de la actividad económica en Bolivia.
Para este propósito se empleó dos tipos de modelos: los primeros de tipo econométrico, con los cuales se establece evidencia empírica soe una relación de largo plazo (test de cointegración y estimación de un modelo de vector de corrección de errores) entre el volumen transaccional en la economía y la evolución del Índice Global de Actividad Económica (IGAE)4; complementariamente, se estimó un modelo de Vectores Autorregresivos (VAR) para la obtención de pronósticos.
El segundo tipo de modelo está basado en Redes Neuronales Artificiales (RNA). Los modelos RNA tienen la capacidad de asimilar dependencias y patrones, con base en un número finito de observaciones; posteriormente este conocimiento puede ser generalizado a observaciones fuera de muestra (Herich et al., 1999). Asimismo, es reconocido que los modelos RNA se constituyen en una valiosa técnica para su aplicación en el campo de la economía, ya que tienen la cualidad de abstraer efectos asimétricos y relaciones no lineales entre variables (McNelis, 2005, p. 7).
La única teoría que apoya la relación entre la actividad económica y la transaccional, se remonta a la teoría cuantitativa del dinero (Fisher, 1911 )5, la cual plantea una equivalencia entre el valor de operaciones en la economía y el nivel de producto. En este sentido, el presente estudio se constituye en el primero de su naturaleza, puesto que además de evaluar la información contenida en el volumen transaccional, la incorpora en modelos de pronóstico que permitan anticipar los movimientos futuros de la actividad económica.
Este documento de trabajo está estructurado de la siguiente manera: después de esta sección introductoria, se presenta una revisión teórica soe la relación entre la actividad transaccional y la económica; en la tercera parte, a través de la estimación de modelos econométricos se muestra evidencia empírica soe dicha relación. En la cuarta parte, se evalúan los pronósticos y sus respectivos errores; y finalmente, se desarrollan las conclusiones y consideraciones de cierre.
II. Revisión teórica
Para analizar la relación entre el valor de las transacciones con dinero electrónico y la actividad económica, se tomó como base referencial la ecuación de cambios de la teoría cuantitativa del dinero presentada por Fisher (1911). En su forma original se tiene:
![]()
donde (M) es el stock de dinero en la economía, (V) la velocidad de circulación del dinero, (P) importe promedio por transacción y (T) número de transacciones realizadas en un año. Con el objeto de lograr una equivalencia con la demanda en la economía, se asumió que (P) correspondía al precio promedio ponderado de cada bien y (T) la suma de los bienes demandados (Q).
En su formulación, Fisher también dividió el stock de dinero de la economía, en billetes y monedas (M) y depósitos vista (M'); además diferenció sus respectivas velocidades de circulación (V,V). Al segundo término del lado izquierdo de la ecuación (2) Fisher lo denominó circulación total de los depósitos (E), la misma que se originaba en los pagos que eran efectuados con instrumentos de pago alternativos al efectivo. A partir de ello Fisher también abordaba una cuestión permanente de la economía monetaria: si la existencia de depósitos bancarios incidía o no en la velocidad total de circulación del dinero.

Inicialmente esta diferenciación en la velocidad de circulación del dinero, no parecía tener mayor relevancia ya que en los períodos precedentes y posteriores cercanos a 1911, los medios de pago alternativos al efectivo se limitaban a instrumentos físicos, como cheques o pagarés, los cuales tenían una rotación similar o menor al dinero en efectivo. Sin embargo, hoy en día el contexto es sustancialmente distinto: las transferencias de dinero tienen un importante componente tecnológico que hace posible que la rotación de los depósitos y contingentes bancarios sea mucho mayor.6 Este tipo de pagos son efectuados con dinero electrónico7. Para ello, los agentes hacen uso de instrumentos electrónicos de pago (tarjetas de crédito, tarjetas de débito, órdenes de pago a través de banca por internet, billeteras móviles) para acceder a sus cuentas y posteriormente efectuar sus transacciones. Los sistemas electrónicos de pago juegan un rol importante en todo este proceso, pues se constituyen en las infraestructuras y canales que hacen posible la circulación del dinero electrónico en las economías.8
De acuerdo con lo señalado, en el presente estudio (E) es aproximado por el valor global de las transacciones con dinero electrónico (DE*)9, las transacciones con billetes y monedas por el saldo del circulante10 (CIRC*) y (PQ) a través del PIB nominal (PY).
![]()
Deflactando por el índice de precios, ambos lados de la identidad (3), aplicando variaciones y finalmente asumiendo la equivalencia entre (Y) e (IGAE) se tiene una relación directamente proporcional entre las variaciones de CIRC, DE e IGAE:

Velocidad de circulación del dinero electrónico
Dado que (DE) representa el valor global de las operaciones con dinero electrónico, también puede ser calculado por el producto entre el stock de dinero constituido en depósitos vista11 (M'2 - CIRC) y un factor de actividad, en este caso la velocidad de circulación del dinero electrónico (VDE).
![]()
De esta manera (VDE) resultaría del cociente entre (DE) y (M'2 - CIRC). Esta identidad, de acuerdo con De Gregorio (2007) incluye transacciones nominales12 en vez del PIB nominal.

El Gráfico 1 muestra la serie de (VDE) para el período junio 2008 -dicieme 2014. En él se observan variaciones importantes entre períodos, que sugieren que (VDE) no tendría un comportamiento invariable en el tiempo como se planteó originalmente.
III. Evidencia empírica
III. 1. Análisis econométrico
En los Gráficos 2 y 3 se presentan las series originales DE13, CIRC e IGAEy desestacionalizadas (DE_SA, CIRC_SA eIGAE_SA)14.

Inicialmente se comprobó la presencia de raíces unitarias en las variables, con las pruebas de Dickey-Fuller Aumentado15 y Phillip-Perron16. Para cada una de ellas se estableció el orden de integración I(1) (véase el Apéndice A.1).
Con el objeto de proponer una relación válida entre las variables señaladas, se verificó la existencia de una relación de largo plazo a través de un test de cointegración y la estimación de un modelo de Vector de Corrección de Errores (VEC).
El test de cointegración de Johansen y Juselius (1990), Johansen (1995) fue aplicado a series no estacionarias. Con esta prueba se evaluó si las variables DE y CIRC son fundamentales para explicar la evolución de IGAE. En el Apéndice A.2 se presentan las pruebas de Traza (Trace Test) y del Máximo Valor Propio (Maximum Eigenvalue Test). Ambos señalan la existencia de un vector de cointegración (al 10% de significancia) entre los logaritmos de IGAE_SA (LIGAE) y DE_SA (LDE). Por su parte, (LCIRC) quedó al margen, dado que no resultó representativa en la relación de largo plazo.
Una vez hallada evidencia soe la cointegración entre variables, se efectuó una prueba de causalidad (Granger) con el fin de establecer cuál variable contiene información histórica que explique el comportamiento de la otra. Los resultados obtenidos señalan que DLDE causa a DLIGAE17 en el sentido Granger al 5% de significancia (Apéndice A.3).
Para la estimación del modelo VEC, se empleó información de frecuencia mensual comprendida entre mayo 2008 y dicieme 2014. La forma VEC y los resultados estimados son los siguientes:
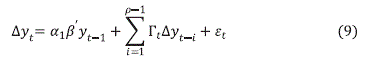
El Cuadro 1 muestra la ecuación de largo plazo donde se aprecia que el signo LDE es coherente con lo esperado según lo expuesto en el marco teórico.
Posteriormente, para el pronóstico de corto plazo de IGAE se estimó un modelo de Vectores Autorregresivos Irrestricto (VAR)18. El modelo fue estimado con base en información de frecuencia mensual. Las variables del modelo corresponden a variaciones porcentuales por mes (VP_IGAEy VP_DE).
A través del test de Dickey-Fuller Aumentado se efectuó la prueba de raíz unitaria a ambas variables en niveles, para lo cual se estableció el orden de integración I(1). Según lo previsto, sus respectivas variaciones porcentuales (primeras diferencias) resultaron ser estacionarias (Apéndice A.4)
Para establecer el número óptimo de rezagos del modelo VAR, se emplearon los criterios de información Akaike (AIC), Schwarz (SC) y Hannan-Quinn (HQ) y el errorde predicción (FPE). Los criterios AIC, HQ y FPE sugieren la inclusión de cuatro (4) rezagos para la construcción del modelo (Apéndice A.5).
El modelo fue sometido a las pruebas de diagnóstico de errores con los test Autocorrelation LM, White Heteroskedasticity y Jarque-Bera. Con estas pruebas se comprobó que el modelo no presenta correlación serial ni heterocedasticidad, y que los residuos se distribuyen normalmente (Apéndice A.6).
Finalmente para evaluar la dinámica de las relaciones entre las variables, se estimaron las funciones impulso-respuesta (FIR). En el Apéndice A. 7 se observa que VP_IGAE responde a shocks de VP_DE, el mismo que tarda dos meses en alcanzar su nivel máximo. También se observa una respuesta importante en el cuarto mes; posteriormente este efecto va disminuyendo paulatinamente.
III.2. Análisis con Redes Neuronales Artificiales (RNA)
Conceptualmente, las RNA son una simulación de las propiedades observadas en los sistemas neuronales biológicos19 a través de modelos matemáticos recreados mediante mecanismos artificiales.
Según Kuan y Liu (1995) una RNA puede ser interpretada como una regresión no lineal, de tipo entrada - salida (input - target) y cuya construcción se basa en una combinación de muchas funciones no lineales básicas a través de una estructura multicapa. En el campo de las series temporales, esta característica hace posible la construcción de modelos que capturen relaciones no lineales y efectos asimétricos entre una variable dependiente (target) yt, y un vector de variables independientes (inputs) xt'.
Para esto, xt' es un vector conformado por (x1t, x2t, ...., xit) que se encuentra en la capa de entrada; este vector es multiplicado por y. (connection strengths). Los resultados obtenidos (unidades ocultas) son componentes de la capa oculta y son sometidas a una función de activación no lineal, por ejemplo una función logística G20. En la capa oculta, las combinaciones lineales de xt'i,j se forman y posteriormente se transforman en un valor entre 0 y 1 de acuerdo con el rango de G. Finalmente, son multiplicados por los ponderadores P¡ para producir yt a través de la capa de salida. Este tipo de RNA es denominado como single hidden layer feedforward network model, ya que contiene una sola capa oculta y la información fluye hacia adelante desde x/hasta yt (Diagrama 1).

De acuerdo con Franses y Van Dyjk (2000), matemáticamente un modelo RNA está definido como:

El término (xt Φ) representa la parte lineal de la relación entre yt y xt', mientras que los componentes logísticos corresponden a la parte no lineal21. El vector xt' está conformado por los rezagos i = 1, ..., n de la variable dependienteyt-i y un conjunto de variables independientes zm paraj= 1... my sus respectivos rezagos zm-p p= 1,..., n.
El aprendizaje de la RNAse da por ajustes graduales de los parámetros θ = (Φr , βt , γt ), con lo cual la red adquiere conocimiento con base en experiencias previas. El conocimiento en (t + 1), depende del conocimiento en el momento (t) más un incremento del conocimiento, , con lo cual θt+1 = θt + Δt. Este incremento está asociado a valores observados, es decir, experiencias ocurridas [(x1,y1),..., (xt,yt)] y nuevas experiencias dadas por los valores (xt+1,yt+1).
En este sentido, el objetivo del aprendizaje de las RNA es hallar los parámetros que minimicen el error. Este error está dado por la sumatoria de cuadrados de la siguiente función:

o

El proceso de aprendizaje de la RNA es de carácter secuencial (Kuan y White, 1994) y puede ser enfocado como un problema de optimización no restringida (Jalil y Misas, 2006). Para este propósito, normalmente son empleados algoritmos recursivos. Entre los más utilizados para el pronóstico de series de tiempo están backpropagation (Werbos, 1974), batch back propagation, conjugate gradient descent (Hestenes y Stiefel, 1952) (Fletcher y Reeves, 1964) y quasi-Newton (Bertsekas, 1982). El objetivo de ellos es estimar el vector de parámetros , que minimice la suma de residuos al cuadrado ![]() y la gradiente asociada
y la gradiente asociada ![]() 22
22
El algoritmo de aprendizaje backpropagation -seleccionado para la estimación del modelo y pronóstico del IGAE- basa su funcionamiento en la actualización de pesos en t0 de acuerdo con los errores obtenidos en t-1 con la r-ésima estimación, de acuerdo con la siguiente identidad:
donde λ es la tasa de aprendizaje y ![]() la matriz de parámetros estimados. La diferencia entre algoritmos radica en la determinación de dicha matriz23.
la matriz de parámetros estimados. La diferencia entre algoritmos radica en la determinación de dicha matriz23.
Para el caso del algoritmo backpropagation el vector gradiente ![]() es calculado de manera recursiva (Apéndice B1).
es calculado de manera recursiva (Apéndice B1).
III. 2.1. Alcance práctico de los modelos RNA
En las últimas dos décadas, el campo de aplicación de los modelos RNA se amplió notablemente en la economía, en particular en lo referente a los pronósticos de corto plazo de variables macroeconómicas. Por ejemplo, Kuan y Liu (1995) elaboraron un estudio de pronósticos del tipo de cambio de seis divisas24; trabajos posteriores también emplearon esta técnica para pronosticar el tipo de cambio del dólar canadiense (Gradojevic y Yang, 2000), del dólar australiano (Kamruzzaman y Sarker, 2004) y del peso colombiano (Jalil y Misas, 2006), entre otros.
Los pronósticos de inflación también han sido abordados desde esta perspectiva: Solera (2005) abarcó esta temática para Costa Rica, mientras que Aristizábal (2006) y Santana (2006) precisaron su estudio para el caso colombiano.
Los modelos RN A también fueron empleados para efectuar pronósticos para la demanda de dinero en efectivo (Misas et al., 2003) y de tasas de interés de títulos soberanos (Enke y Mehdiyev, 2012) (Joseph et al., 2011).
En cuanto a la actividad económica, se destacan los trabajos de Tkacz y Hu (1999) y Gonzales (2000). Ambos elaboraron pronósticos de corto plazo para el comportamiento de la economía canadiense. De igual forma, Salazar (2009) empleó modelos RNA para las proyecciones de PIB en Colombia. Estos autores coinciden en que los pronósticos con RNA superan con un amplio margen a los modelos lineales, lo cual a su vez evidencia la presencia de relaciones asimétricas y no lineales en el comportamiento del PIB.
III. 2.2. Especificación del modelo RNA
La información utilizada para el modelo de RNA consistió en variaciones porcentuales de IGAE (VP_IGAE) y DE (VP_DE) para el período feero 2008 - dicieme 2014. Las observaciones fueron escaladas de acuerdo a ciertas transformaciones para llevarlos al intervalo [0,1 ]25.
El tipo de RNA utilizada en este trabajo, es conocida como de alimentación hacia adelante con una única capa escondida (single hidden layer feedforward network). El tipo de red empleado para el modelo de RNAfue el perceptrón multicapa y el algoritmo de aprendizaje backpropagation.
La arquitectura del modelo fue [7-13-1], es decir, estuvo conformada por una capa de entrada de 7 neuronas, una capa oculta de 13 neuronas y una capa de salida de 1 neurona. De acuerdo con ello, la función de estimación del modelo de RNA estuvo compuesta por las siguientes variables:
![]()
VI. Pronósticos de la actividad económica en Bolivia
En los Gráficos 3 y 4 se muestran la serie original VP_IGAE y los pronósticos arrojados por ambos modelos. Inicialmente es posible observar que el modelo RNA presenta un mejor ajuste que el modelo VAR.

Con el objeto de evaluar la calidad de los pronósticos, se tomó en cuenta los errores de predicción dentro y fuera de la muestra de cada modelo. Para ello, se calcularon el Error de Pronóstico Medio (MAE), Error Porcentual Medio Absoluto (MAPE), Error Cuadrático Medio (RMSE) y U-Theil.
De acuerdo con la totalidad de los indicadores señalados, los pronósticos dentro de la muestra del modelo RNA, registraron errores más bajos que en relación a los pronósticos del modelo VAR. En cuanto a los pronósticos fuera de la muestra, para un período de seis meses, el modelo RNA también resultó más preciso según MAE, RMSE y U-Theil, excepto MAPE que asignó un menor error (2 pp.) al modelo VAR.

A partir de las series obtenidas por los modelos, es posible construir las series de tiempo del pronóstico de IGAE. En ellas se observa que los modelos capturaron adecuadamente las fluctuaciones y comportamiento de la serie original; de igual forma los pronósticos fuera de la muestra resultaron precisos (Gráficos 7 y 8).
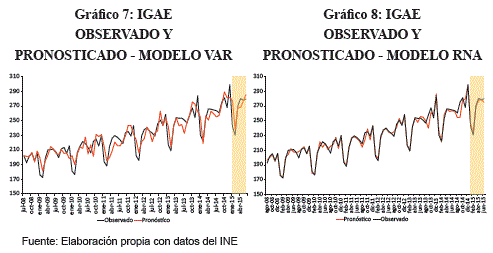
Finalmente, para evaluar la precisión de los pronósticos con el crecimiento económico registrado en los últimos 5 años, se tomó en cuenta el crecimiento del PIB trimestral - variación a doce meses. Complementariamente, se verificó la dirección de los cambios.
En el Gráfico 9 es posible observar que los pronósticos del modelo RNA se mantuvieron en la banda de dispersión (±1 desviación estándar), en tanto que los pronósticos del modelo VAR eventualmente salieron del rango en determinados períodos. Es importante destacar que el error (observado - pronóstico) producido por el modelo RNA para cada período, no superó los 75 pp., en términos absolutos (Cuadro 3).
En cuanto a la dirección de los cambios en las variaciones de la actividad económica, se comprobó que de 19 observaciones posibles, el modelo RNA cometió 5 errores de predicción, en tanto que el modelo VAR incurrió en 6 errores.
V. Conclusiones y consideraciones de cierre
El presente estudio, se constituye en un aporte para la estimación del comportamiento de la actividad económica en el corto plazo, puesto que además de evaluar la información contenida en los pagos con dinero electrónico, la incorpora en modelos de pronóstico que permitan anticipar los movimientos futuros de la actividad económica.
Para ello considera que el volumen transaccional se constituye en una variable que sintetiza información relevante que contribuye al pronóstico de corto plazo de la actividad económica. Este tipo de transacciones incluyen los pagos que son realizados en la economía por conceptos del gasto de consumo, inversión (pública y privada), demanda externa, demanda de bienes y servicios intermedios, entre otros.
Como base teórica se tomó en cuenta la ecuación de cambios de la teoría cuantitativa del dinero, que en su formulación original dividió el stock de dinero de la economía, en billetes y monedas y depósitos vista, e identificó sus respectivas velocidades de circulación. Al producto del stock de depósitos vista y su velocidad, se denominó circulación total de los depósitos. Para su análisis, esta variable fue aproximada por el valor global de las operaciones con dinero electrónico, procesadas por los sistemas de pago en Bolivia.
A través de un test de cointegración se halló evidencia empírica soe una relación a largo plazo, entre el valor de las operaciones con dinero electrónico e IGAE. De igual forma, se estableció el tipo de relación entre las variables a través de un modelo VEC, misma que resultó ser coherente con el marco teórico presentado.
Los modelos de pronóstico de corto plazo VAR y RNA capturaron adecuadamente las fluctuaciones y comportamiento de la serie original.
En términos generales, la exactitud de los pronósticos dentro y fuera de la muestra del modelo RNA fue mayor que en relación a los pronósticos del modelo VAR.
Complementariamente se evaluó la precisión de los pronósticos según el crecimiento del PIB trimestral. Nuevamente, se pudo observar que los pronósticos del modelo RNA fueron más exactos que en relación a los del VAR, puesto que se mantuvieron en la banda de dispersión (±1 desviación estándar). El error (observado-pronóstico) producido por el modelo RNA, para cada período trimestral, no superó los 75 pp., en términos absolutos
En cuanto a la dirección de los cambios de las variaciones de la actividad económica, se comprobó que de 19 observaciones posibles, el modelo RNA cometió 5 errores de predicción, en tanto que, el modelo VAR incurrió en 6 errores.
Para este caso de estudio en particular, el modelo de RNA resultó tener un mejor desempeño en relación al modelo econométrico, debido a que este tipo de modelos tienen la cualidad de abstraer efectos asimétricos y relaciones no lineales entre variables.
Finalmente, se considera que futuros trabajos de investigación podrían abordar metodologías alternativas para pronósticos de corto plazo del IGAE como el nowcasting.
Notas
Se agradece los valiosos comentarios de Oscar Díaz e Ignacio Garrón. El contenido del presente documento es de responsabilidad del autor y no compromete la opinión del Banco Central de Bolivia.
1 Los pronósticos del producto también pueden ser enfocados desde la perspectiva de largo plazo. Para ello existen metodologías como los indicadores líderes -desarrollados por el National Bureau of Economic Research- orientados al estudio del ciclo económico, o indicadores líderes compuestos que abordan aspectos como la desviación de la tendencia y el ciclo de crecimiento.
2 Para el caso boliviano, además de los agregados monetarios M’1 y M’2, la producción de cemento y el consumo de energía eléctrica resultaron ser representativos para pronosticar el crecimiento económico en el corto plazo (Aguilar y Lora, 1999).
3 De acuerdo con los Principios aplicables a infraestructuras del mercado financiero (BIS y IOSCO, 2012), un sistema de pagos se constituye en una infraestructura del mercado financiero que posibilita la transferencia de fondos entre dos o más participantes en un sistema financiero.
4 El IGAE es un indicador coincidente de corto plazo y es publicado periódicamente por el Instituto Nacional de Estadística (INE).
5 El propósito final de esta teoría fue el de establecer una explicación coherente soe los niveles de inflación que podrían alcanzar las economías con base en la cantidad de dinero. Para ello se suponía que la velocidad de circulación del dinero era determinada por aspectos institucionales y tecnológicos que cambian en el tiempo de forma lenta.
6 Estudios al respecto coinciden en que la dinamización de las transacciones como producto de un mayor uso de medios tecnológicos es un factor que incide directamente soe la velocidad de circulación del dinero en las economías (Thornton, 1983) (Mishkin, 2004, p. 518).
7 De acuerdo con el Reglamento de servicios de pago, instrumentos electrónicos de pago, compensación y liquidación (Banco Central de Bolivia, 2015), en Bolivia el dinero electrónico está definido como el valor monetario almacenado en dispositivos electrónicos que circula a través de órdenes de pago. El dinero electrónico es convertible en efectivo a valor nominal a solicitud del titular o beneficiario.
8 Las operaciones efectuadas con dinero electrónico son procesadas y liquidadas a través de los sistemas de pago electrónico bajo distintos esquemas (uto en tiempo real, neto diferido, o híido).
9 De acuerdo con estimaciones del Banco Central de Bolivia (BCB), en la gestión 2014 aproximadamente el 65% del valor global de las transacciones en la economía, fue realizado con dinero electrónico, en tanto que el restante 35% se efectuó con billetes y monedas, por lo que inicialmente, se supondría que (DE) contiene una mayor parte de la información transaccional global.
10 Los pagos con efectivo no requieren de componentes tecnológicos ni de infraestructuras organizadas como los sistemas de pago electrónicos. Por ello resulta complejo estimar el valor de las transacciones que se realizan con billetes y monedas en la economía. La incorporación del circulante como variable proxy se apoya en los preceptos de la teoría de la demanda de dinero, la cual asevera que variaciones en la demanda de saldos reales están asociadas al nivel de transacciones de la economía (Cagan, 1956 y Laidler, 1966).
11 Para el caso boliviano corresponde a las modalidades de caja de ahorro y cuenta corriente.
12 El valor de las transacciones nominales supera al PIB en varias veces, ya que hay bienes que se transan más de una vez, e insumos no incluidos en la medición del PIB (De Gregorio, 2007, p. 398). De acuerdo con esta afirmación, según datos publicados por bancos centrales de la región, la relación entre el valor de las operaciones procesadas por los sistemas electrónicos de pago con el PIB en 2014, alcanzó a 49,9 en asil, 13,2 en México, 11,6 en Colombia, 6,9 en Perú y 3,8 para Bolivia.
13 Los pagos con dinero electrónico incluyen: transferencias interbancarias a través del sistema Liquidación Integrada de Pagos, pagos del gobierno procesados por el Sistema de Pagos del Tesoro, pagos con tarjetas de crédito y débito, pagos con cheques procesados en la cámara de compensación, y órdenes de pago procesadas por la cámara automatizada (ACH).
14 Para ambos casos se detectó un componente estacional. La desestacionalización de las series fue efectuada con el método Census X-11.
15 En la prueba Dickey-Fuller Aumentado se estableció un orden de rezagos de 11 para que los residuos no presenten autocorrelación (Apendice A.1).
16 Los resultados de las pruebas Dickey-Fuller Aumentado y Phillip-Perron poseen propiedades deseables puesto que refutan la existencia de una raíz unitaria.
17 DLDE y DLIGAE corresponden a las primeras diferencias de LDE y LIGAE respectivamente.
18 La forma funcional es la siguiente: , donde es un vector que contiene las variables objeto de predicción; es un vector de k variables que explican adicionalmente las anteriores; y son los coeficientes a estimar y un vector de perturbaciones aleatorias. Esta metodología fundamenta su análisis en un sistema dinámico de ecuaciones, donde la magnitud en t0 de cada variable depende de los valores rezagados (t-1, t-2, t-3,…t-n) de sí misma y de las otras variables involucradas en el sistema.
19 Para comprender el funcionamiento de una RNA es importante entender el funcionamiento biológico del cereo humano. En él, una neurona típica recibe señales a través de un proceso químico denominado sinapsis (unión entre axón y dendritas); a través de este proceso la neurona recoge información procedente de las células vecinas; esta información llega al núcleo donde es procesada hasta generar una respuesta (inhibitoria o estimulante) que es propagada por el axón a otras neuronas. Las conexiones sinápticas tienen una intensidad variable dependiendo de las respuestas. Las neuronas tiene la cualidad de almacenar información y de aprender patrones al momento de reforzar sus conexiones.
20 Su forma funcional
21 Dado que las unidades de las capas ocultas pueden ajustarse a ruidos aleatorios, los parámetros individuales no pueden interpretarse como sucede con los modelos econométricos. Consiguientemente, no es posible medir el tipo de no linealidad, aunque sí la respuesta que es capturada desde los parámetros individuales. Para obtener alguna información de las propiedades de la parte no lineal del modelo, es apropiado inspeccionar la contribución conjunta de los componentes no lineales, esto es: o las contribuciones individuales de cada unidad de la capa oculta: .
22 La gradiente asociada está dada por la siguiente identidad:
23 Por ejemplo el algoritmo Newton-Raphson toma como una matriz hessiana, en tanto que conjugate gradient descent lo asume como una matriz identidad.
24 Dólar estadounidense, lia esterlina, dólar canadiense, marco alemán, yen y franco suizo.
25 Frances y Van Dyjk (2000) proponen la siguiente formula:
Referencias bibliográficas
AGUILAR, M.A. y O. LORA (1999). "Indicadores para anticipar la evolución de la actividad económica", Banco Central de Bolivia, Revista de Análisis 3 (1), pp. 87-119 [ Links ]
ARISTIZÁBAL, M.C. (2006). "Evaluación asimétrica de una red neuronal artificial: aplicación al caso de la inflación en Colombia", Banco de la República de Colombia, Borrador de Economía, 377, feero [ Links ]
BANCO CENTRAL DE BOLIVIA (2015). Reglamento de servicios de pago, instrumentos electrónicos de pago, compensación y liquidación, Resolución de Directorio N° 134/2015 de 28 de julio [ Links ]
BANK FOR INTERNATIONAL SETTLEMENTS and INTERNATIONAL ORGANIZATION OF SUCURITIES COMMISSIONS (2012). Principles for financial market infrastructures, April [ Links ]
BERTSEKAS, D.P. (1982). "Enlarging the Region of Convergence of Newton's Method for Constrained Optimization", Journal of Optimization Theory and Applications, 36 (2), pp. 221-252 [ Links ]
OER, T. (2005). "El dinero como indicador de actividad e inflación en Chile - ¿ya no?", Banco Central de Chile, Documento de trabajo No. 319, mayo [ Links ]
CAGAN, P., "The monetary dynamics of hyperinflation" in FRIEDMAN, M. (Ed.) (1956) Studies in the Quantity Theory of Money, Economics research studies, University of Chicago Economics Research Center, Volume 1,of Studies in Economics, University of Chicago Press, pp.25-117 [ Links ]
DE GREGORIO, J. (2007). Macroeconomía. Teoría y políticas, Pearson-Educación, Santiago, Chile [ Links ]
ENKE, D. and N. MEHDIYEV (2012). "A New Hyid Approach For Forecasting Interest Rates", Procedia Computer Science, 12, pp. 259-264 [ Links ]
ESTRELLA, A. and F. MISHKIN (1996). "Predicting U.S. recessions: financial variables as leading indicators", Federal Reserve Bank of New York, Research Paper No. 9609, May [ Links ]
FISHER, I. (1911). The purchasing power of money. Its determination and relation to credit, interest and crises, The Macmillan Company, Norwood Press, United States of America [ Links ]
FLETCHER, R. and C.M. REEVES (1964). "Function minimization by conjugate gradients", The Computer Journal, 7 (2), pp. 149-154 [ Links ]
FRANSES, P. H. and D. VAN DIJK (2000). Nonlinear Time Series Models in Empirical Finance, Camidge University Press, United States of America [ Links ]
GARCÉS, D. (2002). "Agregados monetarios, inflación y actividad económica en México", Banco de México, Documento de investigación No. 2002-07, ail [ Links ]
GONZALES, S. (2000). "Neural networks for macroeconomic forecasting: a complementary approach to linear regression models", Department of Finance, Working Paper 2000-7 [ Links ]
GRADOJEVIC, N. and J. YANG (2000). "The Application of Artificial Neural Networks to Exchange Rate Forecasting: The Role of Market Microstructure Variables", Bank of Canada, Working Paper No. 2000-23, December [ Links ]
HERICH, R., M. KEILBACH,T. GRAEPEL, P. BOLLMANN-SDORRA, K. OBERMAYER, "Neural Networks in Economics" in ENNER, T. (Ed.) Computational Techniques for Modelling Learning in Economics, Advances in Computational Economics, Springer Science+Business Media, United States, pp. 169-196 [ Links ]
HESTENES, M. and E. STIEFEL (1952). "Methods of Conjugate Gradients for Solving Linear Systems", Journal of Research of the National Bureau ofStandars, 49 (6), pp. 409 - 436 [ Links ]
JALIL, M. y M. MISAS (2006). "Evaluación de pronósticos del tipo de cambio utilizando redes neuronales y funciones de pérdida asimétricas", Banco de la República de Colombia, Borrador de Economía No 376, feero [ Links ]
JOHANSEN, S. and K. JUSELIUS (1990). "Maximum likelihood estimation and inference on cointegration - with applications to the demand for money", Oxford Bulletin of Economics and Statistics, 52 (2), pp. 169-210 [ Links ]
JOHANSEN, S. (1995). Likelihood-based Inference in Cointegrated Vector Autoregressive Models, Oxford University Press, United Kingdom [ Links ]
JOSEPH, A., M. LARRAIN, and E. SINGH (2011). "Predictive Ability of the Interest Rate Spread Using Neural Networks", Procedia Computer Science, 6, pp. 207-212 [ Links ]
KAMRUZZAMAN, J. and R. SARKER (2004). "ANN - Based Forecasting of Foreign Currency Exchange Rates", Neural Information Processing - Letters and Reviews, 3 (2), pp. 49-58 [ Links ]
KUAN, CH.-M. and T. LIU (1995). "Forecasting Exchange Rates Using Feedforward and Recurrent Neural Networks", Journal of Applied Econometrics, 10 (4), pp.347-364 [ Links ]
KUAN, CH.-M. and H. WHITE (1994). "Artificial neural networks: an econometric perspective", Econometric Reviews, 13 (1), pp. 1-91 [ Links ]
LAIDLER, D. (1966). "The Rate of Interest and the Demand for Money - Some Empirical Evidence", Journal of Political Economy, 74 (6), pp. 543-555 [ Links ]
McNELIS, P. (2005). Neural Networks in Finance: Gaining Predictive Edge in the Market, Academic Press Advanced Finance Series, Elsevier Academic Press, United States of America [ Links ]
MISAS, M., E. LOPEZ, C. A. ARANGO, J. N. HERNANDEZ (2003). "La demanda de efectivo en Colombia: una caja negra a la luz de las redes neuronales", Banco de la República de Colombia, Borrador de Economía No 268, novieme [ Links ]
MISHKIN, F. (2004). The Economics of Money, Banking and Financial Markets, Seventh edition, Pearson Addison Wesley, United States of America [ Links ]
SALAZAR, J. M. (2009). "Evaluación de pronóstico de una red neuronal soe el PIB en Colombia", Banco de la República de Colombia, Borrador de Economía No 575, octue [ Links ]
SANTANA, J. C. (2006). "Predicción de series temporales con redes neuronales: una aplicación a la inflación colombiana", Revista Colombiana de Estadística 29 (1),pp. 77-92 [ Links ]
SOLERA, A. (2005). "Pronóstico de inflación en Costa Rica: una estimación con redes neuronales artificiales", Banco Central de Costa Rica, Documento de Trabajo DCS-155-2005, septieme [ Links ]
THORNTON, D. (1983). "Why Does Velocity Matter?", Federal Reserve Bank of St. Louis, Federal Reserve Bank ofSt. Louis Review, pp. 5-13 [ Links ]
TKACZ, G. and S. HU (1999). "Forecasting GDP Growth Using Artificial Neural Networks", Bank of Canada, Working Paper 99-3, January [ Links ]
WERBOS, P. (1974). Beyond regression: newtools for prediction and analysis in the behavioral sciences, a thesis presented to The Committee on Applied Mathematics in partial fulfillment of the requirements forthe degree of Doctor of Philosophy, Harvard University, United States [ Links ]
Apéndices
Apéndice A





Apéndice B