ARTÍCULOS

 

Algoritmo heurístico para el problema de la partición

 

Heuristic algorithm for partition problem

 

 

Lucio Torrico
Instituto de Investigaciones en Informática
Carrera de Informática
Facultad de Ciencias Puras y Naturales
Universidad Mayor de San Andrés
La Paz - Bolivia
Autor de correspondencia:luciotorrico@gmail.com
Presentado: La Paz, 9 de octubre de 2015 | Aceptado: La Paz, 27 de noviembre de 2015

 

 

---

Resumen

En general las soluciones exactas para el problema de la partición se obtienen a través de algoritmos intratables pues el problema es NP. Además de un famoso algoritmo pseudo-polinomial hay, sin embargo, diversos algoritmos heurísticos polinomiales que buscan aproximaciones a una solución exacta (viendo al problema como un caso del subset-sumproblem).

Presentamos un algoritmo heurístico que implementa la idea de ordenar los datos y hacer sumas parciales para obtener nuevos elementos, controlando el crecimiento del número de columnas (para el algoritmo de programación dinámica, el cual hemos cambiado un poco para trabajar con números no secuenciales).Este algoritmo parece comportarse bastante bien para los experimentos realizados.

Palabras clave: Problema de la partición; algoritmo pseudo-polinomial; algoritmo heurístico

---

Abstract

In general, exact solutions to the problem of partition are obtained through algorithms intractable because the problem is NP. Besides a famous pseudo-polynomial algorithm there are, however, a number of polynomial heuristic algorithms that find approximations to an exact solution to the problem (seeing it as a subset-sum problem case).

We present a heuristic algorithm that implements the idea of ordering the data anddo partial sums for get new elements, with growth control of the number of columns (for the dynamic programming algorithm, which we changed a bit to work with non-sequential numbers). This algorithm seems toperform quite wellfor experiments.

Keywords: partition problem, pseudo-polynomial algorithm

---

 

 

Introducción

El problema de la partición es conocido en la algorítmica por ser NP (Garey Michel, Johnson David., 1979).

Hay formas de cálculo no convencionales para solucionar este problema pero sólo las mencionamos debido a que van por otra dirección: la computación molecular por ADN, cuántica, adabiática, de burbujas de jabón, basada en engranajes, etc. (Mihai O., Oana M., 2009).

Presentamos el problema, algunos algoritmos conocidos y nuestra propuesta

 

Métodos

La descripción de los métodos empleados se describe a continuación:

 

El problema

Sea A = { ai,a2,...,a_n } un conjunto de números naturales.

 

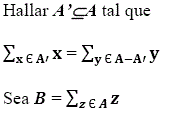
Si B es impar, es claro que el problema no tiene solución.

Si B es par, la suma de los elementos del subconjunto A' buscado debe ser B/2 (Garey Michel, Johnson David., 1979).

Ejemplo: Sea A = {10, 20, 90,100, 200}

La suma de todos los elementos es B=420

Como B es par, estamos buscando un subconjunto A' cuya suma sea B/2=210A' = {10, 200} satisface lo requerido.

Nótese que A-A' = {20, 90, 100} es tal que la suma de sus elementos es también 210.

.

Toth y Martello le llaman "Valué independent Knapsack Problem" o "Stickstacking ProblenT (Ye Yuli, Borodin Alian., 2008). Y otros prefieren decir que es un caso especial del Problema de la Mochila donde los pesos y los valores son iguales (Kellerer H, Pferschy U., D., 2004).

 

Algoritmos conocidos

Un algoritmo exacto por fuerza bruta puede diseñarse seleccionando los subconjuntos tomados de a 1, de a 2, de a 3, ..., de a n . Y verificando si la suma de los elementos suma B/2 Esta idea es claramente intratable.

Otro algoritmo, esta vez heurístico y que apela a la técnica greedy es (Zhao Chenyu. (2011):

1.   Ordenar los elementos de A en orden descendente

2.   Tomar los primeros k=2 elementos y colocarlos en los conjuntos A' y A" respectivamente (A" hará el papel de A-A')

3.   Para los siguientes n-k elementos colocarlos en el conjunto A' o A" que tenga la menor suma

Un algoritmo pseudo-Polinomial (Garey Michel, Johnson David., 1979). Se basa en programación dinámica.

Sea M_nx (B/2) una tabla booleana donde

M(ij) = 1 si existe un subconjunto de A={a1,a2,...,ai} para el cual la suma de todos sus elementos es exactamente j 0 e.o.c

Casos base: Nótese que M(1j)=1si y sólo si j=0 ój=ai

Definiremos

La relación de recurrencia paraes:

Nótese que, cuando la tabla esté llena, la respuesta está en M(n,B/2). Si es 1 el problema de partición tiene solución (un rastreo o traceback puede hallarla), en otro caso no.

Ejemplo:

A = {(11,(12,(13,(14,(15}= {1,9,5,3,8}

La suma de los elementos de A es B=26.

La tabla M llena es:

Y la respuesta es que la partición sí existe:

A' = {ai,a₂,a₄}={1,9,3}

A"=A-A' = {a₃,a₅}={5,8}

En ambos casos la suma de los elementos de cada subconjunto es 13.

• Como las columnas de la matriz van hasta la mitad de la suma de los elementos, si alguno de ellos es muy grande, por ejemplo ai = 2", entonces la matriz será de por lo menos 2ⁿ/2 columnas, haciendo que el llenado de la matriz demore un tiempo O(n-2ⁿ). De ahí que B no sea polinomial en términos del tamaño de la entrada n

 

Algoritmos heurísticos

El problema de la partición también puede verse como un caso especial del subset-sum problem (problema de la suma de subconjuntos) que para el mismo conjunto A={ai,a2,...,a_n} se pregunta si hay un subconjuntotal que (para cualquier c, no sólo para B/2).

Hay algunas ideas heurísticas (Kellerer H., Pferschy U., D., 2004),( PrzydatekBartosz., 2002), (Ye Yuli, Borodin Alian., 2008), (Martello S., Toth P., 1990), que buscan una aproximación a la solución, es decir, hallar un subconjunto A' cuya suma se acerque por debajo a B/2. Aquí las exponemos a grandes rasgos:

Llamaremos Sol a la solución que se construye.

El algoritmo G (algoritmo Greedy) consiste en añadir a1 a Sol si es menor que c, añadir a2 a Sol si la nueva Sol es menor que c, etc.

Nótese que G no ordena los ai c'<-c

 

Aproximación obtenida <- c-c'

El algoritmo G_ext (Greedy extendido) consiste en ejecutar G para hallar Sol por un lado y buscar el máximo de los ai por otro. Luego elegir de entre ambos el valor más cercano a c, que no lo sobrepase.

El algoritmo GR {RandomGreedy) consiste en elegir los m que ingresan a Sol ya no de izquierda a derecha sino al azar (obviamente se añaden mientras su suma no supere c).

Se llama GR(t) a la ejecución t veces del GR y a la selección de la mejor solución de entre la t obtenidas.

Llamaremos GS {Greedy sorteado) a la ejecución (con selecciones de izquierda a derecha) del algoritmo G, pero con la inclusión de un preprocesamiento: Ordenar los ai de modo decreciente. Nótese que esto añade un tiempo O(n-logn).

Martello y Toth proponen correr el algoritmo G,n veces: Primero con los n elementos de A, luego con los n-1 elementos (sin contar ai\ luego con los n-2 elementos (sin contar ai ni a2, etc.).

Y elegir la mejor solución hallada en estasn ejecuciones.

Dado un nivel de alejamiento de la solución (error) € (0<€<l), otros algoritmos dividen los elementos a¿ en pequeños (<€c) y el resto que son los grandes: Y hallan una solución sólo para el conjunto de elementos grandes.

Johnson propuso obtener todos los subconjuntos de a lo más (l/€ -1) elementos grandes (por ej. con €=0.1 serían subconjuntos de a 9 elementos) y con la mejor aproximación seguir asignando los otros elementos pequeños a través del algoritmo G.

Fischetti sugiere hacer un otro procesamiento con los elementos grandes: Agruparlos en q (<l/€ -1) buckets; elegir un elemento de cada bucket; la mejor selección será la que tenga una aproximación mayor a c. Se toma ella y los elementos pequeños se asignan a través del algoritmo G.

Ibarra y Lawler trabajan bajo la idea de escalar los ai grandes y por lo tanto c. Por ejemplo a y donde b= max{ai}

Los elementos pequeños se asignan a través del algoritmo G

Przydatek propone el RGLI(t) {RandomGreedy con mejoramiento local -Local Improvement-): Por cada trial obtiene una solución (por ej. al azar); consideramos cada ai de esa solución y vemos si podemos reemplazarlo por otro aj que noesté pero que haga la nueva suma más cercana a c (sin superarlo). Przydatek se refiere a esto último como el heurístico de Balas y Zemel. Se elige la mejor solución de todos los triáis.

Kellerer también divide los elementos en grandes y pequeños. Estos últimos se asignan a través del algoritmo G

Con los elementos grandes se plantea una idea que aquí la simplificamos mucho:

Los valores de las columnas en la solución de programación dinámica (1..c ) y que hacen intratable al problema, se reducen (relajan) a otro conjunto más pequeño:

Se divide el rango [1, c] en k sub intervalos, y tomando los relevantes: el menor y el mayor valor de cada intervalo.

La complejidad O(n·c) cambiará a O(n·c) = O(n/€).

 

Data-set

Es claro que una elección siempre presente es la asignación aleatoria (o uniforme) de números dentro de un rango.

Kellerer nos muestra otros conjuntos de datos para n entre 5 y 100000 (Kellerer H., Pferschy U., D., 2004). (nótese que son datos pensados para el subset-sum):

pthree. ai aleatoriamente distribuidos en [1,1O³] y c=int(n·10³/4)

psix: a¡ aleatoriamente distribuidos en [1,10⁶] y c=int(n·10⁶/4)

evenodd. ai pares aleatoriamente distribuidos en [1,10³] y c=2·int(n·10³/8)+1

avis: ai=n(n+1)+i y c=n(n+1)·int((n-1)/2)+ n·((n-1)/2)

pl4: ai uniformemente distribuidos en ]1,10¹⁴[ y c=3·10¹⁴

todd: ai=2^k+n+1+2^k+J con k=int(log₂n) y c=B/2

 

La propuesta

Aquí requerimos que los datos sean ordenados. Llamaremos a este el primer nivel.

Con el primer nivel. Efectuaremos varios ciclos: del primer elemento con sus mayores, del segundo elemento con sus mayores, etc., y hallaremos las sumas de estos pares de elementos.

Cada suma será ubicada en una estructura de segundo nivel, respetando el orden.

Con el segundo nivel (y cada nuevo nivel que aparezca): seguiremos hallando sumas de cada elemento con todos los datos del primer nivel que sean mayores al elemento en consideración.

Colocaremos estas sumas en un subsiguiente nivel y manteniendo el orden. En todos los casos las sumas se colocan sólo si no sobrepasan a B/2

Con toda esta cantidad finita -no exponencial- de elementos de todos los niveles aplicamos el algoritmo de programación dinámica con el siguiente cambio:

 

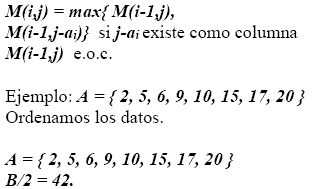
El primer nivel es obvio.

Segundo nivel: 2+5=7, 2+6=8,etc; 5+6=11, 5+9=14, etc.

Tercer nivel: 7+9=18, 7+10=17 ya existe, 7+15=22, etc.

La siguiente tabla muestra todos los valores hallados:

 

Con ellos como columnas junto a la columna con valor 42 hacemos uso del algoritmo basado en programación dinámica aunque reformulado (nótese que las columnas 3, 4,13, 40,41 no existen).

Dicho algoritmo halla una solución en este caso.

 

Desempeño

Las pruebas se hicieron en scripts de Matlab (m-file).

La existencia o no de la columna j-ai se resuelve sin dificultad porque los datos están ordenados.

Las respuestas son exactas para los ejemplos cortos y parecen corresponder con la realidad en ejemplos más grandes (no se han encontrado sets de datos para testeo generalmente aceptados).

El tiempo que demora el algoritmo no es exagerado. De hecho es polinomial.

 

Referencias

Garey Michel, Johnson David. (1979). " Computer^:s and intractability: A Guide to the Theory of NP-Completeness". W.H Freeman and company.         [ Links ]

Kellerer H., Pferschy U., D. (2004). "Knapsack problems". Springer.         [ Links ]

Zhao Chenyu. (2011). "Partition problem: A fast greedy solutiori\ Disponible en: ttp://stackoverflow.com/questions/666946O/the-partition-problem. Visitado el 30/3/2014

Mihai O., Oana M. (2009). "Solving the subset-sum problem with a light-based device". Disponible en http://www.cs.ubbclui.ro/~moltean/optical/optical subset sum.pdf. Visitado el 30/3/2014        [ Links ]

PrzydatekBartosz. (2002). "A FastApproximation Algorithm for the Subset- SumProblem". ftp://ftp.inf.ethz.ch/pub/crypto/publications/Przyda02.ps. Visitado el 30/3/2014        [ Links ]

Ye Yuli, Borodin Alian. (2008). "Priority Algorithms for the Subset-Sum Problem". Disponible  en http://www.cs.toronto.edu/~bor/Papers/prio ritv-subset-sum.pdf. Visitado el 30/3/2014        [ Links ]

Martello S., Toth P. (1990). "Knapsack Problems: Algorithms and Computer Implementations". Wiley.         [ Links ]