ARTÍCULOS

 

Algoritmo heurístico para el problema de la cobertura exacta

 

Heuristic algorithm for exact cover problem

 

 

Lucio Torrico
Instituto de Investigaciones en Informática
Carrera de Informática
Facultad de Ciencias Puras y Naturales
Universidad Mayor de San Andrés
La Paz - Bolivia
Autor de correspondencia: luciotorrico@gmail.com
Presentado: La Paz, 9 de octubre de 2015 | Aceptado: La Paz, 27 de noviembre de 2015

 

 

---

Resumen

En general las soluciones exactas para el exact cover problem se obtienen a través de algoritmos intratables pues el problema es NP. El famoso algoritmo de Knuth (DLX) es uno de ellos. Se presenta un algoritmo heurístico que implementa la idea de tomar los subconjuntos por pares, aplicando una métrica de factibilidad basada en el número de subconjuntos con los que (no) colisionan los subconjuntos de la pareja, y la distancia de Hamming entre ellos.

Al tomar parejas reducimos el tiempo de cálculo, y la elección de los pares más factibles, según la métrica, halla más rápidamente -en promedio- una solución si esta existe. La métrica puede utilizarse también para abandonar la búsqueda, después de cierto límite de factibilidad, conjeturando la no existencia de solución. El mismo parece comportarse bastante bien para los experimentos realizados.

Palabras clave: algoritmo heurístico; cobertura exacta; DLX.

---

Abstract

In general, exact solutions for the exact cover problem are obtained through intractable algorithms because the problem is NP. The famous Knuth's algorithm (DLX) is one ofthem. We present a heuristic algorithm that implements a the idea of taking subsets by pairs, applying a feasibility metric based on the number of subsets that (not)collide with the chosen pair, and the Hamming distance between them.

By taking pairs we reduce the computation time, and the choice of the most feasible pairs, according to the metric, finda solution fáster (on average) , ifit exists. The metric can also be used to abandon the search after a certain feasibility limit, guessing the non existence of solution. His algorithm seems toperform quite wellfor experiments.

Keywords: heuristic algorithm; exact cover; DLX.

---

 

 

Introducción

El problema de la cobertura exacta es conocido en la algorítmica por ser NP Garey M., Johnson D., 1979), (Skiena S., 2008).

Hay formas de cálculo poco convencionales para solucionar este problema pero sólo las mencionamos debido a que van por otra dirección.

La computación: molecular por ADN, con dispositivos de luz, adiabática, etc. (Oltean M., Muntean O., 2008), (Chang Wl., Guo M.,2003),(Choi V.,2011).

Un algoritmo heurístico tiende a hallar (no siempre) una solución factible a través de una idea que asegura un comportamiento razonable en tiempo.

Presentamos el problema, un par de algoritmos conocidos y una nueva propuesta junto a su desempeño.

 

Métodos

Se ha considerado los siguientes aspectos a considerar:

 

El problema

Dados los conjuntos de objetos S₁, S₂,...,S_n. Por ejemplo:

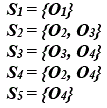
Podemos formar un universo U, uniendo todos esos conjuntos.

En el ejemplo: U={O₁, O₂, O₃, O₄} O bien podemos partir de un universo U y de un conjunto {S₁, S₂,...,S_n} de subconjuntos de U (cuya unión es el universo).

Es claro que podemos trabajar sólo con los subíndices. En el ejemplo: U={1, 2, 3, 4}

S₁={1}
S₂={2,3}
S₃={3,4}
S₄={2,4}
S₅={4}

Un recubrimiento exacto S', es una subcolección S' = {S_i1,...,S_im } tal que cada elemento de U está contenido en exactamente un elemento de S' (Kreher D., StinsonD., 1999).

En el ejemplo S₁, S₂ no es solución pues

En el ejemplo S₁, S₂, S₃, S₄ no es solución pues aunque su unión es U, S₂, S₃ no son disjuntos. En cambioS₁, S₂, S₅ sí soluciona el problema.

Un enunciado formal es: Dado el universo U y un conjunto {S₁, S₂,...,S_n} de subconjuntos de U (cuya unión es el universo), hallar un grupo de subconjuntos S_i1, S_i2,...,S_ik tal que:

Skiena utiliza el nombre de Set Packing para un problema análogo [2].

 

Algoritmos conocidos

Un algoritmo exacto por fuerza bruta puede diseñarse, seleccionando los subconjuntos tomados de a 1 , de a 2, de a 3, ..., de a n .

Verificando disyunción. Esta idea es claramente intratable.

Una versión ingeniosa y algo más rápida (aunque aún intratable) es el llamado algoritmo DLXde Knuth (Knuth D., 2000).

Un algoritmo heurístico es el greedy:

Repetir

Seleccionar el subconjunto más pequeño Eliminar todos los subconjuntos que colisionan con él (los no disjuntos) Hasta que no hayan subconjuntos

Este algoritmo ofrece una aproximación a la solución: la unión de sus subconjuntos, se aproxima -por debajo- a U, aunque no es U en todos los casos.

Siempre que sean aplicables, podemos emplear las llamadas reglas de reducción [9]: Eliminación de subconjuntos vacíos o idénticos, detección de insolubles columnas de ceros, de columnas con un único 1 -y de ahí subconjuntos imprescindibles-, por tanto eliminación de subconjuntos no disjuntos; subsunción de columnas -y de ahí filas estériles-.

 

El algoritmo propuesto

En principio adoptaremos la representación del problema a través una matriz binaria M, donde los subconjuntos candidatos son las filas y cada columna es un elemento del universo.

También supondremos que se hace un preprocesamiento aplicando las reducciones mencionadas antes (estas reducciones podrían aplicarse incluso cuando se obtiene un problema más pequeño fruto de eliminar los subconjuntos de a pares).

La idea es pensar una matriz de distancias denxn donde:

D(i,j)=0 si S_i ∩ S_j = {} (no disyunción o colisión)
D(i,j)=0                 (no disyunción consigo mismo)
D(i,j) = d(S_i, S_j) e.o.c (d es la distancia de Hamming)

Para cada columna (o fila), es decir, para cada subconjunto S_j.

Contabilizamos el número de subconjuntos con los que no colisiona: nc_j.

Contabilizamos el número de subconjuntos con los que si colisiona: sc_j.

Hallamos la diferencia: c_j = nc_j - sc_j.

Para cada par de subconjuntos S_j, S_k disjuntos: Obtenemos un índice de factibilidad o bondad del par así:

F_i,k = c_j + c_k + D(i,k)

Adoptaremos aquí el heurístico de Knuth: Tomar en cuenta la columna con el menor número de 1 's (si hay varias cualquiera).

De todos los pares, seleccionamos los que tengan un subconjunto con un 1 en la columna elegida.

En una lista, ordenamos estos índices de mayor a menor y los consideramos como alternativa de solución en dicho orden decreciente.

Para cada par, eliminamos los subconjuntos, las colisiones, las columnas involucradas, etc. En caso de no solución, hacemos backtracking, hasta un límite de factibilidad prefijado (puede ser muy bajo para tomar en cuenta todos los pares de la lista).

Para cada par elegido de la lista, luego de eliminarlos junto a sus colisiones y columnas involucradas, estamos frente a un nuevo problema más pequeño: aquí podemos usar recurrentemente la idea de índices de factibilidad.

Ejemplo:

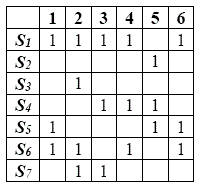
Reducción: La columna 1 es subconjunto de la 6: eliminamos la sexta columna.

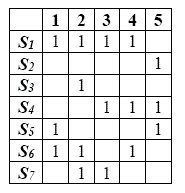
Construimos la matriz D:

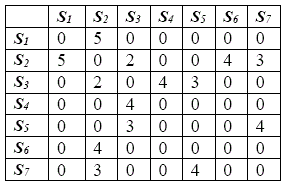
Contabilizamos:

índice de factibilidad por pares disjuntos:

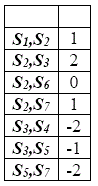
La columna con el menor número de 1's es la primera. Seleccionamos los pares que tengan un subconjunto con un 1 en la columna elegida.

Esta es la lista de pares de subconjuntos ordenada por índice de factibilidad.

Procedemos a utilizar cada par (eliminación, backtracking si no hay solución, etc.) hasta un índice de factibilidad prefijado entre 1 y -2.

S₁, S₂. Es claro que obtendremos una solución con este par.

 

Data set

Se han construido subconjuntos de prueba colocando 1's y '0's aleatoriamente; con diversos valores para n.

Utilizamos además algunos data-set de la librería OR-LIBRARY (Beasley 1, 2012) pero adaptados a la representación aquí tratada.

 

Desempeño

Las pruebas se hicieron en scripts de Matlab (m-file).

La prueba de disyunción de subconjuntos representados como filas binarias puede hacerse así:

not(ismember(1, and(U, M(j,:))))

El cálculo de la distancia de Hamming es trivial.

Nótese que la métrica puede servir para abandonar la búsqueda, después de cierto límite de factibilidad, conjeturando la no existencia de solución.

Con eso en mente, el tiempo que demora el algoritmo es mejor en factores constantes al DLX; nos aproxima heurísticamente a selecciones más óptimas de (pares de) subconjuntos y ofrece una posibilidad argumentada de abort.

Las respuestas son exactas para los ejemplos cortos y parecen corresponder con la realidad en ejemplos más grandes (no se han encontrado seis de datos para testeo generalmente aceptados).

 

Conclusiones

Basados en el planteamiento del problema de cobertura exacta unicost (subconjuntos sin costo/valor) y considerando las reglas de reducción y el algoritmo DLX, se ha ofrecido un algoritmo backtracking que permite, a través de un heurístico en forma

de métrica de factibilidad por pares, hacer una selección más argumentada y más prometedora de los subconjuntos a incluir en la solución.

Además ofrece un mecanismo para detener la búsqueda cuando la factibilidad de los subconjuntos ya es baja, conjeturando una no solución.

El algoritmo parece comportarse bien para los experimentos realizados.

 

Referencias

Garey M., Johnson D. (1979). "Computers and intractability: A Guide to the Theory of NP-Completeness". W.H Freeman and company.         [ Links ]

Skiena S. (2008). "The Algorithm Design Manual". Segunda Edición. Springer.         [ Links ]

Knuth D. (2000). "Dancing links". Millenial Perspectives in Computer Science. Disponible en http://arxiv.org/pdf/cs/0011047vl. Visitado el 30/3/2014.         [ Links ]

Beasley J. (2012). "Or-library". Disponible en: http://people.brunel.ac.uk/~mastjib/ieb/info.html. Visitado el 30/3/2014        [ Links ]

Oltean M., Muntean O. (2008). "Exact Cover with light"         [ Links ]

Chang Wl., Guo M. (2003). "Solving the set cover problem and the problem of exact cover by 3-sets in the Adleman-Lipton model"         [ Links ]

Choi V. (2011). "Different adiabatic quantum optimization algorithms for the NP-complete exact cover and 3SAT problems"         [ Links ]

Kreher D., Stinson D. (1999). "Combinatorial Algorithms : Generation, Enumeration and Search". CRC Press.         [ Links ]

Syslo M., Deo N., Kowalik J. (1983). "Discrete Optimization Algorithms with Pascal Programs". Prentice Hall.         [ Links ]