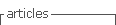ARTÍCULOS ORIGINALES

 

Revisión de modelos para mecanismos de deformación superplástica en aleaciones metálicas

 

Review of models for superplastic deformation mechanisms in metal alloys

 

Revisão de modelos para mecanismos de deformação superplásticas em ligas metálicas

 

 

Mitsuo Osvaldo Ramos Azpeitia
Instituto de Metalurgia, Universidad Autónoma de San Luis Potosí
e mail: mitsuoosvaldo@hotmail.com

 

 

---

Resumen

Los modelos para los mecanismos de deformación superplástica en aleaciones metálicas se basan en el estudio de la respuesta mecánica y en la evaluación de los cambios microestructurales que ocurren debido a la deformación. En los últimos 45 años se han planteado diversos modelos para los mecanismos de deformación superplástica, los cuales están basados principalmente en el estudio de la respuesta mecánica. En estos modelos, generalmente se asume que la deformación se lleva a cabo totalmente en estado estacionario. Este artículo presenta una revisión de los principales modelos propuestos para los mecanismos de deformación superplástica en aleaciones metálicas. Se incluye también un análisis general de los modelos.

Palabras clave: Superplasticidad, mecanismos de deformación, aleaciones metálicas

---

Abstract

The models for the mechanisms of superplastic deformation in metal alloys are based on the study of the mechanical response and on the evaluation of the microstructural changes that happen due to deformation. In the last 45 years many models for superplastic deformation mechanisms have been proposed, which are based primarily on the study of the mechanical response. In these models, it is generally assumed that the deformation is performed entirely in steady state. This article presents a review of the main models proposed for superplastic deformation mechanisms in metallic alloys. It also includes a general analysis of the models.

Keywords: Superplasticity, deformation mechanisms, metallic alloys.

---

Resumo

Os modelos para os mecanismos de deformação superplástica em ligas metálicas são baseados no estudo da resposta mecânica e na avaliação das alterações microestruturais que ocorrem devido à deformação. Nos últimos 45 anos têm sido propostos várias modelos para os mecanismos de deformação superplásticas, que estão baseados principalmente no estudo da resposta mecânica. Nestes modelos, é geralmente aceite que a deformação é realizada inteiramente no estado estacionário. Este artigo apresenta uma revisão dos principais modelos propostos para mecanismos de deformação superplásticos em ligas metálicas. Também se inclui uma análise geral dos modelos.

Palavras chave: Superplasticidade, mecanismos de deformação, ligas metálicas.

---

 

 

Introducción

En general las aleaciones metálicas pueden deformarse plásticamente en tensión hasta un máximo de 50%. Sin embargo, bajo ciertas condiciones, algunas aleaciones pueden exhibir deformaciones mayores al 200%. El fenómeno que produce estas grandes deformaciones se llama superplasticidad [1, 2, 3].

La fluencia es un proceso de deformación plástica que ocurre en los sólidos a elevada temperatura. Esta capacidad de deformación está asociada con tres mecanismos que ocurren a nivel atómico. Los mecanismos son: deslizamiento por movimiento de dislocaciones, resbalamiento de granos y flujo difusional [2]. Se considera que los tres mecanismos ocurren independientemente. Sin embargo en algunos casos, un mecanismo puede ser necesario para permitir el acomodo de otro. Cuando la deformación plástica ocurre en alta temperatura, estos mecanismos son todos térmicamente activados y controlados por difusión.

La superplasticidad se puede considerar como un caso particular del fenómeno de fluencia. Por lo tanto, las relaciones constitutivas para el estudio de la superplasticidad son las mismas que las descritas para la fluencia. La característica más importante del mecanismo de fluencia en alta temperatura es que la rapidez de fluencia (é) varía con el esfuerzo (<r), la temperatura (T) y el tamaño de grano (d) de acuerdo a la relación [1,2,3,4,5]:

 

Donde D es el coeficiente de difusión (= D_o exp -Q/RT), k es la constante de Boltzman, n es el exponente del esfuerzo (n=1/m), G es el modulo de corte, b es el vector de Burguers, p es el exponente de la sensibilidad al tamaño de grano, <r es el esfuerzo de flujo y A es una constante que es función de la microestructura. Esta ecuación es conocida como ecuación Dorn [6]. Cada mecanismo de fluencia puede describirse por esta ecuación y los valores específicos para los parámetros n, p y D. Por lo tanto, para cada aleación metálica, es necesario calcular estos valores para determinar el mecanismo que actúa para llevar a cabo la deformación en estado estacionario.

Durante la deformación superplástica pueden actuar diferentes mecanismos al mismo tiempo, sin embargo solo uno causa la é más rápida y por lo tanto es el mecanismo dominante [7]. La evidencia experimental indica que para la mayoría de los materiales que exhiben comportamiento superplástico, el mecanismo dominante es el GBS(Grain Boundary Slading) [1-5].

Sin embargo para favorecer el mecanismo de GBS y para mantener el contacto entre los granos durante el mismo, es necesario un proceso de acomodo [7, 8, 9]. Este proceso de acomodo es parte del mecanismo de deformación e incluye la migración de bordes de grano, la rotación de los granos y el movimiento de dislocaciones [9, 10, 11]. Generalmente se considera que el proceso de acomodo es la etapa que controla el mecanismo general de la deformación [7]. La mayoría de los modelos difieren en el proceso de acomodo para el GBS.

 

Modelos teóricos para los mecanismos de deformación superplástica

La clasificación de los modelos propuestos para explicar el fenómeno de superplasticidad se puede hacer en función del mecanismo que controla la cinética general del proceso. Los modelos están basados en mecanismos de: flujo difusional, fluencia de dislocaciones, deformación a través del límite de grano y finalmente en la combinación de dos ó más de los mecanismos anteriores. Las características de estos modelos se discuten en las siguientes secciones.

 

Modelos basados en el flujo difusional

El fenómeno de superplasticidad tuvo sus primeras explicaciones en los mecanismos que rigen los procesos de fluencia lenta, debido a que es un fenómeno observado en los materiales deformados en alta temperatura. Actualmente los modelos que se basan en el flujo difusional se consideran más como parte de un proceso de acomodo para otros mecanismos, que como un mecanismo único de deformación.

Estos modelos se basan en la teoría de fluencia difusional, en la cual se considera que bajo la acción de un esfuerzo, un grano experimenta esfuerzos compresivos y de tensión a lo largo de sus bordes. Bajo estas condiciones existe una disminución de vacancias en los bordes que experimentan los esfuerzos compresivos y un exceso de vacancias en los que están sujetos a esfuerzos de tensión, como se muestra en la figura 1. Lo anterior provoca un flujo de vacancias a través de un proceso difusivo para recuperar el equilibrio.

El proceso difusivo puede llevarse a través de la matriz cristalina, en un proceso conocido como fluencia difusional Navarro-Hearring [12, 13], ó a través del límite de grano, en un proceso llamado fluencia difusional Coble [14]. Estos procesos difusivos llevan a la deformación de los granos en la dirección de la aplicación del esfuerzo. Cuando estos procesos actúan, la deformación se lleva a cabo con valores de t < 10^-5 s^-1 [1,15].

Para cada uno de estos procesos, la rapidez de fluencia está dada por la ecuación 1, con valores de n=1 para ambos procesos. En el modelo de Navarro-Hearring, p=2 y D=Dl (Dl es el coeficiente para la difusión a través del grano) [12, 13]. Para el modelo de Coble, p=3 y D=Dgb (Dgb es el coeficiente para la difusión a través del límite de grano) [14]. El valor de la constante A para los modelos de Navarro-Hearring y Coble es 28 y 33 respectivamente [15].

Debido a que las sendas de difusión tanto a través del grano como a través de sus límites son independientes, la fluencia es controlada por el proceso de difusión más rápido [15]. Se ha establecido que debido a que la energía de activación para llevar a cabo el proceso de difusión a través del límite de grano es menor que la necesaria para procesos a través del grano, la velocidad de fluencia a través de un mecanismo tipo Coble debe de ser mayor que la obtenida mediante un mecanismo tipo Navarro-Hearring [1].

 

Además de los mecanismos anteriores se ha propuesto un tercer mecanismo de fluencia llamado Harper-Dorn [16,17,18]. Este mecanismo se propuso para explicar resultados en aleaciones base aluminio que no mostraron dependencia con el tamaño de grano (p = 0) y donde se obtuvieron rapideces de fluencia mayores a las predichas por los mecanismos de Navarro-Hearring y de Coble [16, 17, 18]. Sin embargo existe controversia al respecto, pues existe dificultad para la reproducción de estos resultados [19].

Las ideas de los modelos anteriores fueron consideradas por Ashby y Verrall [20], para plantear un modelo que describe a la región II del comportamiento sigmoidal como una región de transición entre dos mecanismos que ocurren a baja y elevada É. En el primer mecanismo la deformación es resultado de un flujo de material asistido por procesos de difusión similares a los planteados en los modelos de Navarro-Hearring y Coble, mientras que en el segundo mecanismo se plantea que la deformación se favorece por un proceso de trepado de dislocaciones controlado por difusión, el cual provoca la elongación de los granos.

El modelo considera que la compatibilidad de los granos se mantiene mediante un momentáneo pero complejo cambio de forma asistido por procesos de difusión [20]. Sin embargo Spingarn y Nix [21], concluyeron que las sendas de difusión que se plantearon originalmente no pueden ser posibles físicamente, por lo cual propusieron sendas de difusión alternativas que modifican el mecanismo original.

Los modelos de Ashby y Verrall [20] y de Spingarn y Nix [21], concuerdan con algunas de los aspectos microestructurales observados en los materiales superplásticos y también en la dependencia del valor de m con respecto a la rapidez de deformación. Sin embargo actualmente ya no se consideran importantes debido a que predicen erróneamente algunos aspectos tales como los valores de la energía de activación y la dependencia del esfuerzo con la temperatura y el tamaño de grano.

 

Modelos basados en la fluencia por dislocaciones

Estos modelos consideran que, como resultado de la operación de un mecanismo de GBS, se produce una concentración de esfuerzos que es relevada por el movimiento de dislocaciones. Este movimiento de dislocaciones sirve a su vez como proceso de acomodo para que continúe el GBS. Las diferencias entre los modelos radican en la forma en que estas dislocaciones se producen y se mueven durante el proceso de acomodo para el GBS.

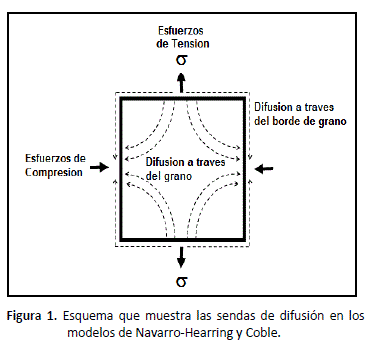
Ball y Hutchinson [22], propusieron que en la región II grupos de cuatro granos se resbalan como una unidad hasta que un grano que está orientado desfavorablemente obstruye el proceso, generando así una concentración de esfuerzos que es posteriormente relevada por la generación de dislocaciones dentro del grano que obstruye el proceso. Estas dislocaciones se mueven a través del grano y se apilan sobre el límite de grano, hasta que disminuye la concentración de esfuerzos, deteniendo así la generación de dislocaciones. Las dislocaciones apiladas en el límite de grano pueden después trepar a lo largo de este límite para aniquilarse. En la figura 2 se esquematiza como se llevan a cabo estos procesos.

 

Mukherjee [23], propuso una modificación del modelo anterior en la cual consideró que el resbalamiento se lleva a cabo de manera individual y no en grupos de cuatro granos. En este modelo se considera que las dislocaciones generadas por defectos en los límites de grano atraviesan el grano y se apilan en el límite para después trepar y aniquilarse como se esquematiza en la figura 3. Para ambos modelos, la rapidez con que se lleva a cabo el resbalamiento es controlada por la rapidez de trepado de la dislocación principal (la primera al frente). Los modelos anteriores predicen correctamente la dependencia de la é con respecto a la temperatura en la región II, pero no predicen la existencia de la región I. Por lo tanto, estos modelos no explican la relación sigmoidal observada experimentalmente.

 

Posteriormente Mukherjee [24], realizó una modificación a su modelo original. En este nuevo modelo se propone que la rapidez con que se lleva cabo el resbalamiento es controlada por la rapidez con que se lleva a cabo el movimiento de las dislocaciones en el límite de grano. Este movimiento es originado por un proceso de trepado y deslizamiento de dislocaciones [24]. Además, este modelo propone que la compatibilidad entre los granos se mantiene mediante un proceso de trepado de dislocaciones de borde controlado por difusión que ocurre a lo largo del límite de grano. Para este modelo la combinación del GBS y del proceso de trepado de dislocaciones provoca un rearreglo de los granos que evita la elongación de los mismos durante la deformación superplástica.

Otro modelo que contempla la fluencia de dislocaciones es el propuesto por Hayden, Floreen y Goodell [25]. En este modelo, se propone que el GBS es controlado por la rapidez con que fluyen las dislocaciones intragranulares creadas en el límite de grano en puntos triples y en defectos dentro del grano (escalones). Al igual que otros modelos, las dislocaciones atraviesan el grano por medio del trepado y el deslizamiento para después trepar individualmente, sin formar apilamiento, hacia el límite del grano que se opone al resbalamiento, donde son aniquiladas. Este modelo postula además la existencia de una temperatura crítica, donde ocurre una transición en el mecanismo de difusión que controla el trepado de las dislocaciones.

 

Modelos basados en la deformación a través de los límites de grano

Estos modelos están basados en las observaciones microestructurales que coinciden en que la deformación se lleva a cabo mediante procesos relacionados con el resbalamiento a través de los límites de grano (GBS). Estos modelos postulan que el resbalamiento de granos es un proceso que necesita un subsecuente proceso de reacomodo. La mayoría de los modelos consideran que la etapa que controla la rapidez de fluencia es este acomodo y el modo de deformación que ocurre en él.

Uno de los primeros modelos que consideró al GBS como principal mecanismo de deformación fue el de Hazzledine y Newbury [26]. En este modelo se considera que el GBS es acomodado por la continua deformación de los granos. Sin embargo, esta deformación es oscilatoria con el tiempo, por lo que la forma equiaxiada de los granos siempre se mantiene. El modelo considera que los granos se mueven continuamente y que como resultado de este movimiento, se forman huecos que son llenados con granos que emergen de capas adyacentes. El modelo postula que la rapidez de deformación del grano es del orden de 0,625 veces la rapidez del resbalamiento de los granos. El modelo considera que la deformación de los granos es resultado de la operación simultánea de los mecanismos de difusión y de GBS.

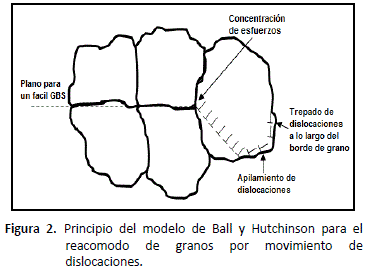
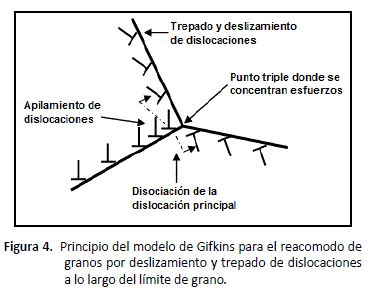
Otro modelo que considera al GBS como el principal mecanismo de deformación es el propuesto por Gifkins [27, 28]. Este modelo considera que el GBS se lleva a cabo por el movimiento de dislocaciones en el límite de grano que se apilan en puntos triples, provocando una concentración de esfuerzos que es relevada por la disociación de la dislocación principal (la primera al frente). Las dislocaciones resultantes son capaces de moverse en los otros dos límites que forman el punto triple, permitiendo de esta manera el acomodo para el GBS. Estas nuevas dislocaciones trepan dentro ó cerca de estos dos límites hasta encontrarse una con otra, al ocurrir esto pueden aniquilarse ó combinarse. El esquema de este mecanismo se observa en la figura 4.

 

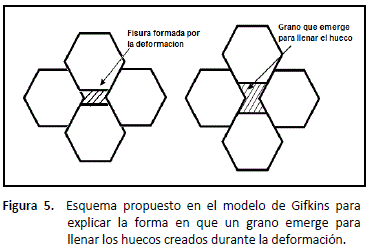
Gifkins consideró las ideas formuladas por el modelo de Hazzledine y Newbury [26], para plantear que en su modelo la compatibilidad entre los granos durante la deformación se mantiene mediante un proceso en el cual, material que emerge proveniente de planos adyacentes (nuevos granos), llena huecos creados durante la deformación [27, 28]. Estos nuevos granos llenan los huecos a través de un mecanismo de GBS. Gifkins reportó observaciones microestructurales que confirman un incremento en el área superficial durante la deformación. Esta evidencia confirma la propuesta de que existe un re-arreglo de los granos que contempla este proceso en el cual los granos emergen. En la figura 5 se ilustra esquemáticamente como ocurre este re-arreglo de los granos.

Gifkins también utilizó en su modelo una analogía con la forma de las capas de la tierra para describir la región adyacente al límite de grano y el interior del mismo. En dicha descripción llamada de "manto y corazón", se asume que el proceso de acomodo para el GBS ocurre dentro de la capa viscosa exterior (manto) que rodea al centro rígido del grano (corazón). Si se considera un arreglo bidimensional de granos con forma hexagonal, el ancho del manto debe de ser 0,07 el tamaño del grano para que el GBS ocurra (ver figura 6).

 

 

Este concepto fue utilizado posteriormente por Mayo y Nix [29], para describir un modelo para la deformación superplástica. En este modelo se propone que el espesor del manto es función del esfuerzo aplicado y por lo tanto puede ser variable. El modelo propone que la deformación en el manto ocurre más rápido que en el corazón y que el tamaño de este manto cambia en función de la deformación y es inversamente proporcional al esfuerzo aplicado. También considera que el corazón del grano se deforma por un proceso de fluencia asistido por el trepado de dislocaciones.

En el modelo de Kaibyshev y Valiev [30], también se considera al movimiento de dislocaciones como parte del proceso de acomodo para un mecanismo de GBS. En este modelo se propone que existen procesos de endurecimiento por deformación y de recuperación. También se propone que existe el movimiento de dos tipos de dislocaciones de borde. En el primer tipo (intrínsecas), se apilan en puntos triples iniciando la generación de dislocaciones de red, mientras que en el segundo tipo (extrínsecas), son formadas como resultado del trepado de dislocaciones en los límites de grano. El movimiento de las dislocaciones extrínsecas lleva al resbalamiento de los límites de grano, mientras que la aniquilación de estas dislocaciones en el límite de grano y/ó en los puntos triples, es la responsable del proceso de recuperación. Este modelo se ajusta muy bien en la descripción de la relación entre el esfuerzo y la rapidez de deformación, aunque con valores de m menores a los reportados experimentalmente.

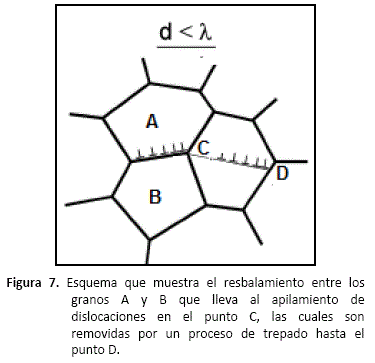
Posteriormente Valiev y Langdon [9, 31, 32], propusieron un modelo de resbalamiento de límites de grano acomodado por un proceso que está basado en el modelo de Ball y Hutchinson [22]. Este resbalamiento ocurre por el movimiento de dislocaciones a lo largo de los límites, las cuales son bloqueadas por obstáculos tales como puntos triples ó escalones. Este bloqueo puede generar deslizamiento en los granos vecinos, lo cual a su vez ayuda a que las dislocaciones del límite de grano se muevan y apilen en el primer obstáculo que se oponga a este movimiento como se ilustra en la figura 7.

En este modelo, la velocidad de resbalamiento es controlada por la velocidad a la cual las dislocaciones son removidas por un proceso de trepado de dislocaciones similar al planteado por Ball y Hutchinson [22]. El modelo plantea que para que ocurra un flujo plástico a través de los límites de grano, el tamaño de grano (d) debe de ser menor al tamaño de los sub-granos que se pueden formar en equilibrio (X) durante la deformación. El proceso de formación de sub-granos es función del esfuerzo.

La mayor objeción de los modelos anteriores es que el apilamiento de dislocaciones no se observa con frecuencia, además de que estas dislocaciones podrían no ser muy estables a elevadas temperaturas. Tomando en cuenta lo anterior, Padmanabhan y col. [33, 34, 35, 36, 37], propusieron un modelo que contempla que el flujo superplástico en condiciones óptimas (condiciones que permiten mayor deformación), resulta de un resbalamiento que ocurre en los imites de grano asistido por un flujo difusivo a lo largo de la interfaz. Se propone que este proceso es asistido también por una migración local del límite de grano.

 

Modelos mixtos

Actualmente el fenómeno de superplasticidad es todavía complejo de explicar, debido a que ningún modelo propuesto hasta ahora puede adecuarse en su totalidad a las observaciones experimentales realizadas. Debido a lo anterior, se ha concluido que posiblemente más de un mecanismo opera en secuencia durante el flujo superplástico. Se han planteado modelos mixtos que proponen que el mecanismo de deformación incluye la operación de más de un mecanismo como los descritos en secciones anteriores. Para los modelos mixtos es difícil realizar un planteamiento matemático debido a la dificultad que representa determinar la contribución de cada uno de los diferentes mecanismos.

Entre los primeros modelos mixtos que se propusieron destaca el de Baudelet y col. [38, 39, 40]. Este modelo fue propuesto para aleaciones bifásicas en donde los granos de una fase más dúctil son inicialmente alargados. El modelo plantea que durante la deformación, los granos alargados se resbalan a lo largo de sus límites para alinearse y orientarse en una dirección paralela a la de la aplicación de la carga. Estos granos alargados se separan a lo largo de sus límites internos (sub-fronteras) con el incremento de la deformación, permitiendo que alcancen una configuración equiaxiada. Se propone que el proceso para separar los granos requiere un esfuerzo mayor al que proporciona un flujo en estado estacionario, lo cual resulta en una etapa de ablandamiento al inicio de la deformación. Este modelo contempla que la deformación en estado estacionario resulta de la combinación de un mecanismo de GBS y de un proceso que permite la deformación de la fase más suave.

Ghosh [41], planteó un modelo que incorpora las ideas del modelo de Gifkins [27, 28], de manto y corazón. En este modelo se propone que la deformación se lleva a cabo por la combinación de dos mecanismos, uno que permite la deformación en la región del manto por procesos de deslazamiento y trepado de dislocaciones; y otro que origina una deformación del corazón del grano mediante procesos de fluencia de dislocaciones. Este modelo difiere al de Gifkins [27, 28], en que no considera que exista un transporte de masa extensivo. En este modelo las dislocaciones pueden ser generadas por discontinuidades tales como esquinas de granos, puntos triples y escalones de límites de grano. Para este modelo, la rapidez de deformación resulta de la contribución de ambos mecanismos. El modelo además contempla que existe un crecimiento de grano durante la deformación.

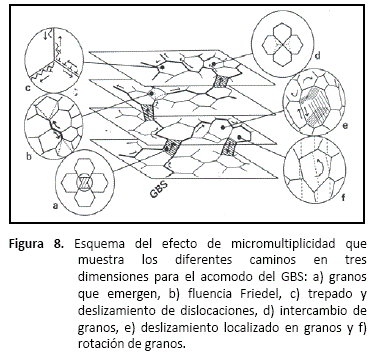
En los años ochenta Gifkins [42], sugirió la idea de que diversos "micro-mecanismos" ocurren de manera local para llevar a cabo el proceso de acomodo para el GBS a diferencia de los modelos clásicos que proponen un único mecanismo. Esta propuesta llevó al concepto del "efecto de micro-multiplicidad" que se esquematiza en la figura 8. Este efecto provee diferentes caminos en tres dimensiones para acomodar el GBS. El modelo plantea que los micromecanismos para el acomodo pueden ser: la migración de límites de grano, el trepado y deslizamiento de dislocaciones, la rotación de granos y el movimiento de granos para que estos emerjan. Este concepto parece ser el más adecuado para explicar las diferencias entre los modelos clásicos y los resultados experimentales observados.

 

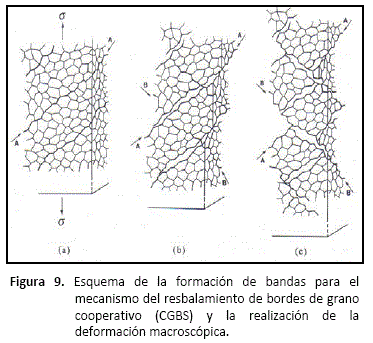
Pschenichniuk y col. [43-45], plantearon un modelo basado en evidencia experimental que demuestra la existencia de un fenómeno de resbalamiento cooperativo de límites de grano (Cooperative Grain Boundary Sliding, CGBS). En el CGBS la

deformación se lleva a cabo por el movimiento de grupos de granos que forman bandas, las cuales se mueven por el efecto de esfuerzos de corte a través de los límites cooperativos de estas bandas, como se muestra en la figura 9.

 

La formación de bandas se realiza a través de mecanismos que permiten el acomodo para el alineamiento de los límites de grano en un plano común de deslizamiento. Estos mecanismos comprenden procesos de migración local de límites ó de puntos triples y el deslizamiento intragranular. En el modelo, la rapidez de deformación total es la suma de las rapideces de deformación debidas a un proceso de difusión por fluencia, al CGBS y al deslizamiento intragranular. Para cada proceso, el modelo plantea una serie de ecuaciones que toman en consideración parámetros tales como los valores del vector de Burguers en las dislocaciones de red y de limite de grano, los coeficientes de difusión para procesos a través de la red y el límite de grano; además de la cantidad de bandas que se pueden formar para el CGBS. El número de bandas que se pueden formar es función de la probabilidad de que un límite de grano participe en la formación de bandas de deformación. Este modelo contempla los efectos de los cambios microestructurales que se dan durante la deformación. El modelo se ha utilizado para explicar el mecanismo de deformación de diversas aleaciones [46-48].

 

Análisis de los modelos propuestos

La mayoría de los modelos descritos anteriormente se plantearon para explicar la relación sigmoidal entre el esfuerzo de flujo y la rapidez de deformación observada en diversas aleaciones que presentan comportamiento superplástico. Algunos de estos modelos consideraron las observaciones microestructurales, mientras que otros solo fueron propuestos teóricamente sin una validación experimental. Hasta el momento no existe un modelo único que se adecue a todas las observaciones micro y macroestructurales realizadas sobre el fenómeno de superplasticidad. Un análisis de los modelos se presenta a continuación:

1.    Los modelos propuestos hasta el momento son generales y se pueden considerar validos para una gran variedad de aleaciones. Sin embargo, para una aleación determinada, se puede obtener información adicional de su comportamiento superplástico que complemente el modelo general y describa de mejor manera su mecanismo de deformación.

2.    Los modelos propuestos hasta el momento consideran que el mecanismo que actúa para alcanzar condiciones de flujo estacionario, sigue actuando durante todo el proceso de deformación hasta la fractura del material. Sin embargo algunas aleaciones pueden presentar cambios macro y microestructurales que sugieren modificaciones en el mecanismo de deformación. Por lo tanto, el modelo planteado para estas aleaciones debe de considerar la posibilidad de que estas modificaciones ocurren durante la deformación.

3.    Los modelos propuestos hasta el momento consideran que el mecanismo propuesto para una región superplástica (región II), es válido para todo el intervalo de rapidez de deformación que comprende esta región. Sin embargo, si se desea utilizar una aleación para una aplicación industrial, es necesario conocer el mecanismo preciso que actúa en diversas condiciones específicas para establecer aquellas que permitan que un proceso de termoformado se lleve a cabo de una manera óptima.

 

Referencias

1.     PADMANABHAN K. A., DAVIES G. J. Superplasticity. Springer, Germany, 1980, p. 7-37, 50-110.        [ Links ]

2.     NIEH T.G., WADSWORTH J., SHERBY O; Superplasticity in metals and ceramics. Cambridge University Press, U.K., 1997, p. 22-53.        [ Links ]

3.     PADMANABHAN K. A., VASIN R. A., ENIKEEV F.U. Superplastic flow: phenomenology and mechanics. Springer, Germany; 2001; p. 5-27.        [ Links ]

4.     MUKHERJEE A. K. "Superplasticity in metals, ceramics and Intermetallics" In: Mater. Sci. Tech. Vol. 6: Plastic Deformation and Fracture of Materials. Edited by Mughrabi H., VCH, Germany, 1993, p. 407-460.        [ Links ]

5.     LANGDON T. G. "Seventy-five years of superplasticity: historic developments and new opportunities". J. Mater. Sci. 44, 2009, 5998-6010.        [ Links ]

6.     DIETER G. E. Mechanical Metallurgy. 3er edition. Mc Graw-Hill, 1988, p. 184-219, 274-314, 432-470.        [ Links ]

7.    ARIELI A., MUKHERJEE K. "The rate controlling deformation mechanisms in superplasticity - a critical assessment" Metall. Trans. A 13,1982, 717-731.        [ Links ]

8.     LANGDON T. G. "The mechanical properties of superplastic materials" Metall. Trans. 13 A, 1982, 689-702.        [ Links ]

9.     LANGDON T. G. "Grain boundary sliding revisited: developments in sliding over four decades". J. Mater. Sci. 41, 2006, 597-609.        [ Links ]

10.   KASHYAP B. P., ARIELI A., MUKHERJEE A. K. "Review: microstructural aspects of superplasticity". J. Mater. Sci. 20, 1985, 2661-2686.        [ Links ]

11.   ZELIN M. G. "Processes of microstructural evolution during superplastic deformation". Mater. Charact. 37, 1996, 311-329.        [ Links ]

12.   NAVARRO F. R. N. "Deformation of Crystals by the Motion of Single Ions". Physical Society Bristol Conference Report. 1948, 75-90.        [ Links ]

13.   HEARRING C. "Diffusional viscosity of a polycrystalline solid". J. Appl. Phys. 21. 1950, 437-445.        [ Links ]

14.   COBLE R. L. "Model for boundary diffusion-controlled creep in polycrystalline materials". J. Appl. Phys. 34. 1963, 1679-1682.        [ Links ]

15.   CHOKSHI A. H. "Diffusion creep in metals and ceramics: extension to nanocrystals". Mater. Sci. Eng. A. 2008, 485-491.        [ Links ]

16.   HARPER J., DORN J. E. "Viscous creep of aluminum near its melting temperature". Acta Metall. 5.1957, 654-665.        [ Links ]

17.   LANDON T. G. "Creep at Low Stresses: An Evaluation of Diffusion Creep and Harper-Dorn Creep as Viable Creep Mechanisms". Metall. Trans. 33A, 2002, 257-259.        [ Links ]

18.   CHENG Y. C., CHAUHAN M., MOHAMED F. A. "Uncovering the mystery of Harper-Dorn creep in metals". Metall. Trans. 40A, 2009, 80-90.        [ Links ]

19.   BLUM W., EISENLOHR P., BREUTINGER F. "Understanding creep—a review". Metall. Trans. 33A, 2002, 291-303.        [ Links ]

20.   ASHBY M. F., VERRALL R. A. "Diffusion-accommodated flow and superplasticity". Acta Metall. 21,1973,149-163.        [ Links ]

21.   SPINGARN J. R., NIX W. D. "Diffusional creep and diffusionally accommodated grain rearrangement". Acta Metall. 26, 1977, 1389-1398.        [ Links ]

22.   BALL A., HUTCHINSON M. M. "Superplasticity in the aluminium-zinc eutectoid". Metall. Sci. J. 3,1969,1-7.        [ Links ]

23.   MUKHERJEE A. K. "The rate controlling mechanism in superplasticity". Mat. Sci. Eng. 8,1971, 83-89.        [ Links ]

24.   MUKHERJEE A. K. In: "Grain Boundaries in Engineering Materials". Walter J. L. et al. eds. Claitor Publishing, Baton Rouge, L.A, 1975; p. 93-98.        [ Links ]

25.   HAYDEN H. W., FLOREEN S., GOODELL P. D. "The Deformation. Mechanisms of Superplasticity". Metall. Trans. 3, 1972, 833-842.        [ Links ]

26.   HAZZLEDINE P. M., NEWBURY D. E. En: Grain Boundary Structure and Properties. Chadwhick GA, Smith DA Eds, Academic Press London, UK, 1976, p 235-240.        [ Links ]

27.   GIFKINS R. C. "Grain-Boundary Sliding and its Accommodation During Creep and Superplasticity". Metall. Trans. A7, 1976, 1225-1232.        [ Links ]

28.   GIFKINS R. C. "Grain rearrangements during superplastic deformation". J. Mat. Sci. 13,1978,1926-1936.        [ Links ]

29.   MAYO J., NIX W. D. "Direct observation of superplastic flow mechanisms in torsion". Acta Metall. 37,1989,1121-1134.        [ Links ]

30.   KAIBYSHEV O. A., VALIEV R. Z., EMALETDINOV A. K. "Deformation mechanisms and the theory of structural superplasticity of metals". Phys. Sta. Sol. A 90, 1985, 197-206.        [ Links ]

31.   VALIEV R. Z., LANGDON T. G. "An investigation of the role of intragranular dislocation strain in the superplastic Pb-62% Sn eutectic alloy". Acta Metall. Mater. 41, 1993, 949-954.        [ Links ]

32.   LANGDON T. G. "A unified approach to grain boundary sliding in creep and superplasticity". Acta Metall. Mater. 42, 1994, 2437-2443.        [ Links ]

33.   PADMANABHAN K. A., SCHLIPF J. "Model for grain boundary sliding and its relevance to optimal structural superplasticity: part 1 -theory". Mater. Sci. Tech. 12,1996, 391-399.        [ Links ]

34.   ASTANIN V. V., FAIZOVA S. N., PADMANABHAN K. A. "Model for grain boundary sliding and its relevance to optimal structural superplasticity: part 2 - evidence for cooperative grain/interphase boundary sliding and plane interface formation". Mater. Sci. Tech. 12,1996, 489-494.        [ Links ]

35.   ASTANIN V. V., PADMANABHAN K. A., BHATTACHARYA S. S. "Model for grain boundary sliding and its relevance to optimal structural superplasticity: part 3 - effect of flow localization and specimen thickness on superplasticity in alloy Supral 100". Mater. Sci. Tech. 12,1996, 545-550.        [ Links ]

36.   VENKATESH T. A., BHATTACHARYA S. S., PADMANABHAN K. A., SCHLIPF J. "Model for grain boundary sliding and its relevance to optimal structural superplasticity: part 4 -experimental verification" Mater. Sci. Tech. 12, 1996, 635-643.        [ Links ]

37.   ENIKEEV F. U., PADMANABHAN K. A., BHATTACHARYA S. S. "Model for grain boundary sliding and its relevance to optimal structural superplasticity: part 5 - a unique numerical solution and its reliability". Mater. Sci. Tech. 15, 1999, 673-682.        [ Links ]

38.   SUERY M., BAUDALET B. "Flow stress and microstructure in superplastic 60/40 brass". J. Mater. Sci. 8,1973, 363-369.        [ Links ]

39.   HERRIOT G., BAUDALET B., JONAS J. J. "Superplastic behaviour of two-phase Cu-P alloys". Acta Metal. 24, 1976, 687-694.        [ Links ]

40.   HOMER C., LECHTEN J. P., BAUDALET B. "Superplastic behavior of welded specimens of the titanium alloy TA6V". Metall. Trans. A 8.1977; 1191-1193.        [ Links ]

41.   GHOSH A. K. "A new physical model for superplastic flow". Mater. Sci. For. 170-173, 1994; 39-46.        [ Links ]

42.   GIFKINS R. C. "Mechanisms of Superplasticity"; In: . R. RAJ AND M.F. ASHBY (eds). Superplastic forming of structural alloys, plastic forming of structural alloys. Metallurgical Society of AIME, New York: 1982, pp 3-26.        [ Links ]

43.   PSCHENICHNIUK A. I., ASTANIN V. V., KAIBYSHEV O. A. "The model of grain boundary sliding simulated by intragranular slip". Philos. Mag. 77, 1998,1093-1106.        [ Links ]

44.   ASTANIN V. V., KAIBYSHEV O. A., PSCHENICHNIUK A. I. "Cooperative process during superplastic deformation" Mater. Sci. Forum 243-2454,1997, 41-46.        [ Links ]

45.   ASTANIN V. V., KAIBYSHEV O. A., FAIZOBA S. N. "Cooperative grain boundary sliding during superplastic deformation". Scripta Metal. Mater. 25,1991, 2663-2668.        [ Links ]

46.   ZELIN M. G., DUNLAP M. R., ROSEN R., MUKHERJEE A. K. "The direct observation of grain boundary sliding and migration during migration superplastic deformation of Lead tin eutectic in shear". J. Appl. Phys. 74,1993,1-11.        [ Links ]

47.   ASTANIN V. V., KAIBYSHEV O. A. "Cooperative grain boundary sliding and superplastic flow nature. Mater. Sci. Forum 170-172, 1994, 23-28.        [ Links ]

48.   ZELIN M. G., MUKHERJEE A. K. "Cooperative phenomena at grain boundaries during superplastic flow". Acta Metall. 43,1995, 2359-2372.        [ Links ]